Monoidal category
Encyclopedia
In mathematics
, a monoidal category (or tensor category) is a category
C equipped with a bifunctor
which is associative, up to
a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism. (The associated natural isomorphisms are called natural because they together satisfy certain coherence condition
s which state that all the relevant diagrams commute.) Monoidal categories are, therefore, a loose categorical analog of monoid
s in abstract algebra
.
Ordinary tensor product
makes vector space
s, abelian group
s, R-modules
, or R-algebras
, monoidal categories. Monoidal categories can be seen as a generalization of these and other examples.
In category theory
, monoidal categories can be used to define the concept of a monoid object and an associated action on the objects of the category. They are also used in the definition of an enriched category
.
Monoidal categories have numerous applications outside of category theory proper. They are used to define models for the multiplicative fragment of intuitionistic linear logic
. They also form the mathematical foundation for the topological order
in condensed matter. Braided monoidal categories have applications in quantum field theory
and string theory
.
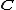 equipped with
equipped with
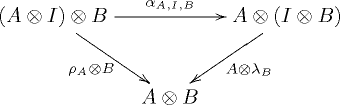
The coherence conditions for these natural transformations are:
commutes
;
commutes
;
It follows from these three conditions that any such diagram (i.e. a diagram whose morphisms are built using ,
, 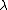 ,
, 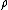 , identities and tensor product) commutes: this is Mac Lane's
, identities and tensor product) commutes: this is Mac Lane's
"coherence theorem
".
A strict monoidal category is one for which the natural isomorphisms α, λ and ρ are identities. Every monoidal category is monoidally equivalent
to a strict monoidal category.
For any commutative ring R, the category of R-algebras is monoidal with the tensor product of algebras
as the product and R as the unit.
The category of pointed spaces is monoidal with the smash product
serving as the product and the pointed 0-sphere (a two-point discrete space) serving as the unit.
The category of all endofunctors on a category C is a strict monoidal category with the composition of functors as the product and the identity functor as the unit.
Bounded-above meet semilattices
are strict symmetric monoidal categories: the product is meet and the identity is the top element.
strict monoidal category Σ(C) can be constructed as follows:
This operation Σ mapping category C to Σ(C) can be extended to a strict 2-monad on Cat.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a monoidal category (or tensor category) is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C equipped with a bifunctor
- ⊗ : C × C → C
which is associative, up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism. (The associated natural isomorphisms are called natural because they together satisfy certain coherence condition
Coherence condition
In mathematics, and particularly category theory a coherence condition is a collection of conditions requiring that various compositions of elementary morphisms are equal...
s which state that all the relevant diagrams commute.) Monoidal categories are, therefore, a loose categorical analog of monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
.
Ordinary tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
makes vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, R-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, or R-algebras
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
, monoidal categories. Monoidal categories can be seen as a generalization of these and other examples.
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, monoidal categories can be used to define the concept of a monoid object and an associated action on the objects of the category. They are also used in the definition of an enriched category
Enriched category
In category theory and its applications to mathematics, enriched category is a generalization of category that abstracts the set of morphisms associated with every pair of objects to an opaque object in some fixed monoidal category of "hom-objects" and then defines composition and identity solely...
.
Monoidal categories have numerous applications outside of category theory proper. They are used to define models for the multiplicative fragment of intuitionistic linear logic
Linear logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
. They also form the mathematical foundation for the topological order
Topological order
In physics, topological order is a new kind of order in a quantum state that is beyond the Landau symmetry-breaking description. It cannot be described by local order parameters and long range correlations...
in condensed matter. Braided monoidal categories have applications in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
.
Formal definition
A monoidal category is a category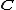 equipped with
equipped with
- a bifunctor
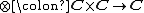 called the tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
called the tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
or monoidal product, - an object
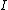 called the unit object or identity object,
called the unit object or identity object, - three natural isomorphisms subject to certain coherence conditionCoherence conditionIn mathematics, and particularly category theory a coherence condition is a collection of conditions requiring that various compositions of elementary morphisms are equal...
s expressing the fact that the tensor operation- is associative: there is a natural isomorphism
 , called associator, with components
, called associator, with components 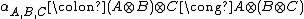 ,
, - has
 as left and right identity: there are two natural isomorphisms
as left and right identity: there are two natural isomorphisms 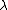 and
and 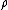 , respectively called left and right unitor, with components
, respectively called left and right unitor, with components 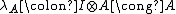 and
and 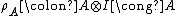 .
.
- is associative: there is a natural isomorphism
The coherence conditions for these natural transformations are:
- for all
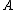 ,
, 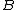 ,
, 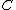 and
and 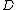 in
in 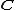 , the diagramDiagram (category theory)In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
, the diagramDiagram (category theory)In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
;
- for all
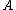 and
and 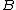 in
in 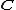 , the diagramDiagram (category theory)In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
, the diagramDiagram (category theory)In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
;
It follows from these three conditions that any such diagram (i.e. a diagram whose morphisms are built using
 ,
, 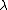 ,
, 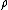 , identities and tensor product) commutes: this is Mac Lane's
, identities and tensor product) commutes: this is Mac Lane'sSaunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
"coherence theorem
Coherence theorem
In mathematics and particularly category theory, a coherence theorem is a tool for proving a coherence condition. Typically a coherence condition requires an infinite number of equalities among compositions of structure maps...
".
A strict monoidal category is one for which the natural isomorphisms α, λ and ρ are identities. Every monoidal category is monoidally equivalent
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
to a strict monoidal category.
Examples
- Any category with finite productProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
s is monoidal with the product as the monoidal product and the terminal object as the unit. Such a category is sometimes called a cartesian monoidal category. - Any category with finite coproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s is monoidal with the coproduct as the monoidal product and the initial objectInitial objectIn category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
as the unit. - R-Mod, the category of modules over a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R, is a monoidal category with the tensor product of modulesTensor product of modulesIn mathematics, the tensor product of modules is a construction that allows arguments about bilinear maps to be carried out in terms of linear maps...
⊗R serving as the monoidal product and the ring R (thought of as a module over itself) serving as the unit. As special cases one has:Category of vector spacesIn mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, with the one-dimensional vector space K serving as the unit. - Ab, the category of abelian groupsCategory of abelian groupsIn mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
, with the group of integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s Z serving as the unit.
Tensor product of algebras
In mathematics, the tensor product of two R-algebras is also an R-algebra. This gives us a tensor product of algebras. The special case R = Z gives us a tensor product of rings, since rings may be regarded as Z-algebras....
as the product and R as the unit.
Smash product
In mathematics, the smash product of two pointed spaces X and Y is the quotient of the product space X × Y under the identifications ∼ for all x ∈ X and y ∈ Y. The smash product is usually denoted X ∧ Y...
serving as the product and the pointed 0-sphere (a two-point discrete space) serving as the unit.
Semilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
are strict symmetric monoidal categories: the product is meet and the identity is the top element.
Free strict monoidal category
For every category C, the freeFree object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
strict monoidal category Σ(C) can be constructed as follows:
- its objects are lists (finite sequences) A1, ..., An of objects of C;
- there are arrows between two objects A1, ..., Am and B1, ..., Bn only if m = n, and then the arrows are lists (finite sequences) of arrows f1: A1 → B1, ..., fn: An → Bn of C;
- the tensor product of two objects A1, ..., An and B1, ..., Bm is the concatenation A1, ..., An, B1, ..., Bm of the two lists, and, similarly, the tensor product of two morphisms is given by the concatenation of lists.
This operation Σ mapping category C to Σ(C) can be extended to a strict 2-monad on Cat.
See also
- Many monoidal categories have additional structure such as braiding, symmetry or closureClosed monoidal categoryIn mathematics, especially in category theory, aclosed monoidal category is a context where we can take tensor products of objects and also form 'mapping objects'. A classic example is the category of sets, Set, where the tensor product of sets A and B is the usual cartesian product A \times B, and...
: the references describe this in detail. - Monoidal functorMonoidal functorIn category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a...
s are the functors between monoidal categories which preserve the tensor product and monoidal natural transformationMonoidal natural transformationSuppose that and are two monoidal categories and:\to and :\toare two lax monoidal functors between those categories....
s are the natural transformations, between those functors, which are "compatible" with the tensor product. - There is a general notion of monoid object in a monoidal category, which generalizes the ordinary notion of monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
. In particular, a strict monoidal category can be seen as a monoid object in the category of categories Cat (equipped with the monoidal structure induced by the cartesian product). - A monoidal category can also be seen as the category B(□, □) of a bicategoryBicategoryIn mathematics, a bicategory is a concept in category theory used to extend the notion of category to handle the cases where the composition of morphisms is not associative, but only associative up to an isomorphism. The notion was introduced in 1967 by Jean Bénabou.Formally, a bicategory B...
B with only one object, denoted □. - Rigid categoriesRigid categoryIn category theory, a branch of mathematics, a rigid category is a monoidal category where every object is rigid, that is, has a dual X* and a morphism 1 → X ⊗ X* satisfying natural conditions. The category is called right rigid or left rigid according to whether it has right duals or...
are monoidal categories in which duals with nice properties exist. - Autonomous categoriesAutonomous categoryIn mathematics, an autonomous category is a monoidal category where dual objects exist.-Definition:A left autonomous category is a monoidal category where every object has a left dual. An autonomous category is a monoidal category where every object has both a left and a right dual...
are monoidal categories in which inverses exist. - A category C enrichedEnriched categoryIn category theory and its applications to mathematics, enriched category is a generalization of category that abstracts the set of morphisms associated with every pair of objects to an opaque object in some fixed monoidal category of "hom-objects" and then defines composition and identity solely...
in a monoidal category M replaces the notion of a set of morphisms between pairs of objects in C with the notion of an M-object of morphisms between every two objects in C.