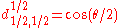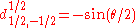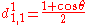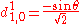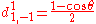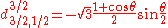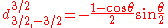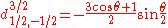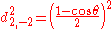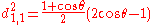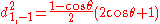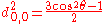Wigner D-matrix
Encyclopedia
The Wigner D-matrix is a matrix in an irreducible representation of the groups SU(2) and SO(3). The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotor
s. The matrix was introduced in 1927 by Eugene Wigner.
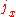 ,
, 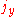 ,
, 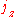 be generators of the Lie algebra
be generators of the Lie algebra
of SU(2) and SO(3). In quantum mechanics
these
three operators are the components of a vector operator known as angular momentum. Examples
are the angular momentum of an electron
in an atom, electronic spin
,and the angular momentum
of a rigid rotor
. In all cases the three operators satisfy the following commutation relations,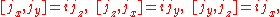
where i is the purely imaginary number
and Planck's constant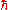 has been put equal to one. The operator
has been put equal to one. The operator
is a Casimir operator
of SU(2) (or SO(3) as the case may be).
It may be diagonalized together with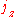 (the choice of this operator
(the choice of this operator
is a convention), which commutes with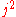 . That is, it can be shown that there is a complete set of kets with
. That is, it can be shown that there is a complete set of kets with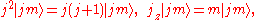
where and
and  . (For SO(3) the quantum number
. (For SO(3) the quantum number 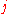 is integer.)
is integer.)
A rotation operator can be written as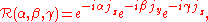
where and
and  are Euler angles
are Euler angles
(characterized by the keywords: z-y-z convention, right-handed frame, right-hand screw rule, active interpretation).
The Wigner D-matrix is a square matrix of dimension with
with
general element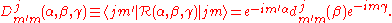
The matrix with general element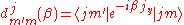
is known as Wigner's (small) d-matrix.
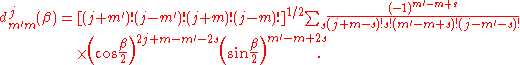
The sum over s is over such values that the factorials are nonnegative.
Note: The d-matrix elements defined here are real. In the often-used z-x-z convention of Euler angles, the factor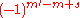 in this formula is replaced by
in this formula is replaced by 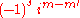 , causing half of the functions to be purely imaginary. The realness of the d-matrix elements is one of the reasons that the z-y-z convention, used in this article, is usually preferred in quantum mechanical applications.
, causing half of the functions to be purely imaginary. The realness of the d-matrix elements is one of the reasons that the z-y-z convention, used in this article, is usually preferred in quantum mechanical applications.
The d-matrix elements are related to Jacobi polynomials
 with nonnegative
with nonnegative  and
and  . Let
. Let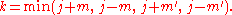
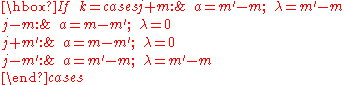
Then, with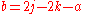 , the relation is
, the relation is

where
that can be formulated concisely by introducing the following operators with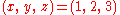 ,
,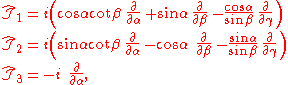
which have quantum mechanical meaning: they are space-fixed rigid rotor
angular momentum operators.
Further,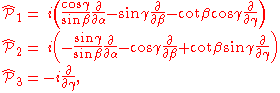
which have quantum mechanical meaning: they are body-fixed rigid rotor
angular momentum operators.
The operators satisfy the commutation relations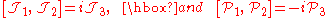
and the corresponding relations with the indices permuted cyclically.
The satisfy anomalous commutation relations
satisfy anomalous commutation relations
(have a minus sign on the right hand side).
The two sets mutually commute,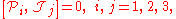
and the total operators squared are equal,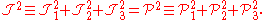
Their explicit form is,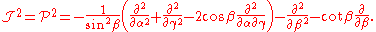
The operators act on the first (row) index of the D-matrix,
act on the first (row) index of the D-matrix,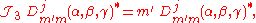
and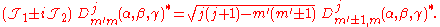
The operators act on the second (column) index of the D-matrix
act on the second (column) index of the D-matrix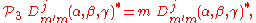
and because of the anomalous commutation relation the raising/lowering operators
are defined with reversed signs,
Finally,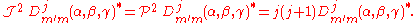
In other words, the rows and columns of the (complex conjugate) Wigner D-matrix span
irreducible representations of the isomorphic Lie algebra's
generated by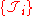 and
and 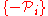 .
.
An important property of the Wigner D-matrix follows from the commutation of
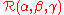 with the time reversal operator
with the time reversal operator
 ,
,
or
Here we used that is anti-unitary (hence the complex conjugation after moving
is anti-unitary (hence the complex conjugation after moving
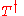 from ket to bra),
from ket to bra), 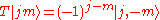 and
and 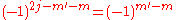 .
.
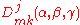 form a complete set
form a complete set
of orthogonal functions of the Euler angles ,
, 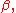 and
and 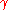 :
: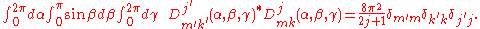
This is a special case of the Schur orthogonality relations
.
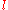 , the D-matrix elements with second index equal to zero are proportional
, the D-matrix elements with second index equal to zero are proportional
to spherical harmonics
and associated Legendre polynomials
, normalized to unity and with Condon and Shortley phase convention: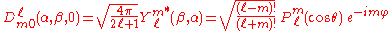
This implies the following relationship for the d-matrix: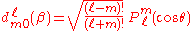
When both indices are set to zero, the Wigner D-matrix elements are given by ordinary Legendre polynomials: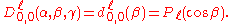
In the present convention of Euler angles, is
is
a longitudinal angle and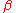 is a colatitudinal angle (spherical polar angles
is a colatitudinal angle (spherical polar angles
in the physical definition of such angles). This is one of the reasons that the z-y-z
convention is used frequently in molecular physics.
From the time-reversal property of the Wigner D-matrix follows immediately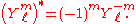
There exists a more general relationship to the spin-weighted spherical harmonics
: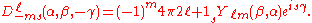
 we have
we have  where
where  is the Bessel function
is the Bessel function
and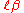 is finite.
is finite.
for j=1/2
for j=1
for j=3/2
for j=2
Wigner d-matrix elements with swapped lower indices are found with the relation: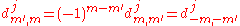 .
.
Rigid rotor
The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
s. The matrix was introduced in 1927 by Eugene Wigner.
Definition Wigner D-matrix
Let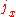 ,
, 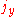 ,
, 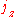 be generators of the Lie algebra
be generators of the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of SU(2) and SO(3). In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
these
three operators are the components of a vector operator known as angular momentum. Examples
are the angular momentum of an electron
in an atom, electronic spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
,and the angular momentum
of a rigid rotor
Rigid rotor
The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
. In all cases the three operators satisfy the following commutation relations,
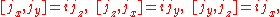
where i is the purely imaginary number
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
and Planck's constant
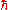 has been put equal to one. The operator
has been put equal to one. The operator
is a Casimir operator
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
of SU(2) (or SO(3) as the case may be).
It may be diagonalized together with
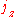 (the choice of this operator
(the choice of this operatoris a convention), which commutes with
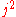 . That is, it can be shown that there is a complete set of kets with
. That is, it can be shown that there is a complete set of kets with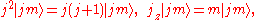
where
 and
and  . (For SO(3) the quantum number
. (For SO(3) the quantum number  is integer.)
is integer.)A rotation operator can be written as
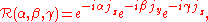
where
 and
and  are Euler angles
are Euler anglesEuler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
(characterized by the keywords: z-y-z convention, right-handed frame, right-hand screw rule, active interpretation).
The Wigner D-matrix is a square matrix of dimension
 with
withgeneral element
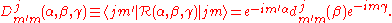
The matrix with general element
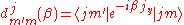
is known as Wigner's (small) d-matrix.
Wigner (small) d-matrix
Wigner gave the following expression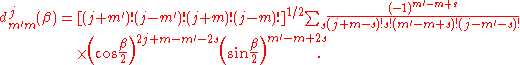
The sum over s is over such values that the factorials are nonnegative.
Note: The d-matrix elements defined here are real. In the often-used z-x-z convention of Euler angles, the factor
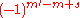 in this formula is replaced by
in this formula is replaced by 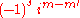 , causing half of the functions to be purely imaginary. The realness of the d-matrix elements is one of the reasons that the z-y-z convention, used in this article, is usually preferred in quantum mechanical applications.
, causing half of the functions to be purely imaginary. The realness of the d-matrix elements is one of the reasons that the z-y-z convention, used in this article, is usually preferred in quantum mechanical applications.The d-matrix elements are related to Jacobi polynomials
Jacobi polynomials
In mathematics, Jacobi polynomials are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight ^\alpha ^\beta on the interval [-1, 1]...
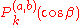 with nonnegative
with nonnegative  and
and  . Let
. Let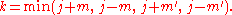
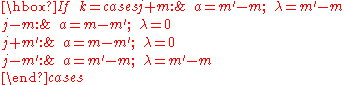
Then, with
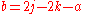 , the relation is
, the relation is
where

Properties of Wigner D-matrix
The complex conjugate of the D-matrix satisfies a number of differential propertiesthat can be formulated concisely by introducing the following operators with
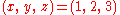 ,
,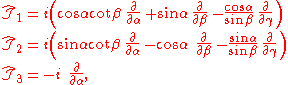
which have quantum mechanical meaning: they are space-fixed rigid rotor
Rigid rotor
The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
angular momentum operators.
Further,
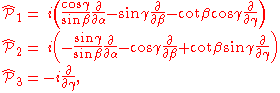
which have quantum mechanical meaning: they are body-fixed rigid rotor
Rigid rotor
The rigid rotor is a mechanical model that is used to explain rotating systems.An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space three angles are required. A special rigid rotor is the linear rotor which isa 2-dimensional object, requiring...
angular momentum operators.
The operators satisfy the commutation relations
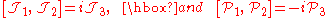
and the corresponding relations with the indices permuted cyclically.
The
 satisfy anomalous commutation relations
satisfy anomalous commutation relations(have a minus sign on the right hand side).
The two sets mutually commute,
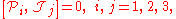
and the total operators squared are equal,
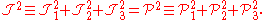
Their explicit form is,
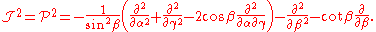
The operators
 act on the first (row) index of the D-matrix,
act on the first (row) index of the D-matrix,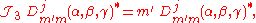
and
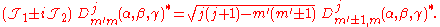
The operators
 act on the second (column) index of the D-matrix
act on the second (column) index of the D-matrix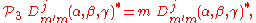
and because of the anomalous commutation relation the raising/lowering operators
are defined with reversed signs,

Finally,
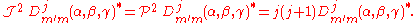
In other words, the rows and columns of the (complex conjugate) Wigner D-matrix span
irreducible representations of the isomorphic Lie algebra's
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
generated by
 and
and 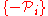 .
.An important property of the Wigner D-matrix follows from the commutation of
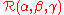 with the time reversal operator
with the time reversal operator ,
,
or

Here we used that
 is anti-unitary (hence the complex conjugation after moving
is anti-unitary (hence the complex conjugation after moving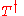 from ket to bra),
from ket to bra), 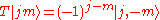 and
and 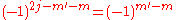 .
.Orthogonality relations
The Wigner D-matrix elements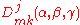 form a complete set
form a complete setof orthogonal functions of the Euler angles
 ,
, 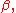 and
and 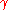 :
: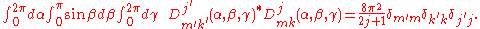
This is a special case of the Schur orthogonality relations
Schur orthogonality relations
In mathematics, the Schur orthogonality relations express a central fact about representations of finite groups.They admit a generalization to the case of compact groups in general, and in particular compact Lie groups, such as therotation group SO....
.
Relation to spherical harmonics and Legendre polynomials
For integer values of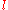 , the D-matrix elements with second index equal to zero are proportional
, the D-matrix elements with second index equal to zero are proportionalto spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
and associated Legendre polynomials
Associated Legendre polynomials
In mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation\,y -2xy' + \left\,y = 0,\,or equivalently...
, normalized to unity and with Condon and Shortley phase convention:
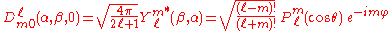
This implies the following relationship for the d-matrix:
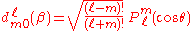
When both indices are set to zero, the Wigner D-matrix elements are given by ordinary Legendre polynomials:
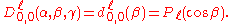
In the present convention of Euler angles,
 is
isa longitudinal angle and
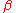 is a colatitudinal angle (spherical polar angles
is a colatitudinal angle (spherical polar anglesin the physical definition of such angles). This is one of the reasons that the z-y-z
convention is used frequently in molecular physics.
From the time-reversal property of the Wigner D-matrix follows immediately
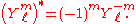
There exists a more general relationship to the spin-weighted spherical harmonics
Spin-weighted spherical harmonics
Spin-weighted spherical harmonics are generalizations of the standard spherical harmonics and—like the usual spherical harmonics—are functions on the sphere. Unlike ordinary spherical harmonics, the spin-weighted harmonics are U gauge fields rather than scalar fields: mathematically, they take...
:
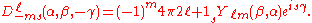
Relation to Bessel Function
In the limit when we have
we have  where
where  is the Bessel function
is the Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
and
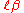 is finite.
is finite.Table of d-matrix Elements
Using sign convention of Wigner, et al. the d-matrix elements for j=1/2, 1, 3/2, and 2 are given below.for j=1/2
for j=1
for j=3/2
for j=2
Wigner d-matrix elements with swapped lower indices are found with the relation:
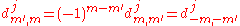 .
.