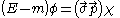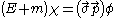Dirac spinor
Encyclopedia
In quantum field theory
, the Dirac spinor is the bispinor
in the plane-wave
solution
of the free Dirac equation
,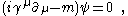
where (in the units )
)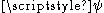 is a relativistic
is a relativistic
spin-1/2 field
, is the Dirac spinor
is the Dirac spinor
related to a plane-wave with wave-vector ,
, ,
, is the four-wave-vector of the plane wave, where
is the four-wave-vector of the plane wave, where 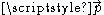 is arbitrary,
is arbitrary, are the four-coordinates in a given inertial frame of reference.
are the four-coordinates in a given inertial frame of reference.
The Dirac spinor for the positive-frequency solution can be written as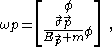
where is an arbitrary two-spinor,
is an arbitrary two-spinor,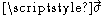 are the Pauli matrices
are the Pauli matrices
,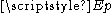 is the positive square root
is the positive square root 
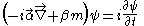
In order to derive the form of the four-spinor we have to first note the value of the matrices α and β:
we have to first note the value of the matrices α and β:
These two 4×4 matrices are related to the Dirac gamma matrices. Note that 0 and I are 2×2 matrices here.
The next step is to look for solutions of the form ,
,
while at the same time splitting ω into two two-spinors: .
.
 .
.
This matrix equation is really two coupled equations:
Solve the 2nd equation for and one obtains
and one obtains .
.
Solve the 1st equation for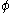 and one finds
and one finds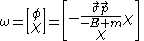 .
.
This solution is useful for showing the relation between anti-particle and particle.
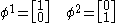
and
are
Using these, one can calculate:
 . These spinors are denoted as u:
. These spinors are denoted as u:
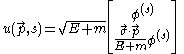
where s = 1 or 2 (spin "up" or "down")
Explicitly,
 are defined as particles having negative energy and propagating backward in time. Hence changing the sign of
are defined as particles having negative energy and propagating backward in time. Hence changing the sign of  and
and  in the four-spinor for particles will give the four-spinor for anti-particles:
in the four-spinor for particles will give the four-spinor for anti-particles:
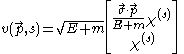
Here we choose the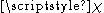 solutions. Explicitly,
solutions. Explicitly,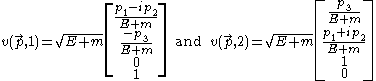


where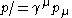 (see Feynman slash notation)
(see Feynman slash notation)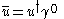
that are used as spin
and charge
operators
.
that are in common use in the physics literature. The Dirac matrices are typically written as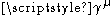 where
where  runs from 0 to 3. In this notation, 0 corresponds to time, and 1 through 3 correspond to x, y, and z.
runs from 0 to 3. In this notation, 0 corresponds to time, and 1 through 3 correspond to x, y, and z.
The + − − − signature is sometimes called the west coast
metric, while the − + + + is the east coast
metric. At this time the + − − − signature is in more common use, and our example will use this signature. To switch from one example to the other, multiply all by
by  .
.
After choosing the signature, there are many ways of constructing a representation in the 4×4 matrices, and many are in common use. In order to make this example as general as possible we will not specify a representation until the final step. At that time we will substitute in the "chiral"
or "Weyl"
representation as used in the popular graduate textbook An Introduction to Quantum Field Theory by Michael E. Peskin
and Daniel V. Schroeder.
direction for our electron or positron. As with the example of the Pauli algebra discussed above, the spin direction is defined by a unit vector in 3 dimensions, (a, b, c). Following the convention of Peskin & Schroeder, the spin operator for spin in the (a, b, c) direction is defined as the dot product of (a, b, c) with the vector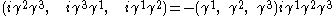

Note that the above is a root of unity
, that is, it squares to 1. Consequently, we can make a projection operator from it that projects out the sub-algebra of the Dirac algebra that has spin oriented in the (a, b, c) direction:
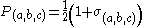
Now we must choose a charge, +1 (positron) or −1 (electron). Following the conventions of Peskin & Schroeder, the operator for charge is , that is, electron states will take an eigenvalue of −1 with respect to this operator while positron states will take an eigenvalue of +1.
, that is, electron states will take an eigenvalue of −1 with respect to this operator while positron states will take an eigenvalue of +1.
Note that is also a square root of unity. Furthermore,
is also a square root of unity. Furthermore,  commutes with
commutes with  . They form a complete set of commuting operators for the Dirac algebra. Continuing with our example, we look for a representation of an electron with spin in the (a, b, c) direction. Turning
. They form a complete set of commuting operators for the Dirac algebra. Continuing with our example, we look for a representation of an electron with spin in the (a, b, c) direction. Turning  into a projection operator for charge = −1, we have
into a projection operator for charge = −1, we have

The projection operator for the spinor we seek is therefore the product of the two projection operators we've found:

The above projection operator, when applied to any spinor, will give that part of the spinor that corresponds to the electron state we seek. Therefore, to write down a 4×1 spinor we take any non zero column of the above matrix. Continuing the example, we put (a, b, c) = (0, 0, 1) and have

and so our desired projection operator is
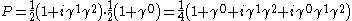
The 4×4 gamma matrices used in Peskin & Schroeder (Weyl representation) are
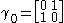
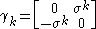
for k = 1, 2, 3 and where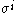 are the usual 2×2 Pauli matrices
are the usual 2×2 Pauli matrices
. Substituting these in for P gives

Our answer is any non zero column of the above matrix. The division by two is just a normalization. The first and third columns give the same result:
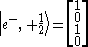
More generally, for electrons and positrons with spin oriented in the (a, b, c) direction, the projection operator is
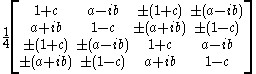
where the upper signs are for the electron and the lower signs are for the positron. The corresponding spinor can be taken as any non zero column. Since the different columns are multiples of the same spinor.
the different columns are multiples of the same spinor.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the Dirac spinor is the bispinor
Bispinor
In physics, bispinor is a four-component object which transforms under the ⊕ representation of the covariance group of special relativity...
in the plane-wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
solution

of the free Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
,
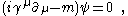
where (in the units
 )
)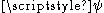 is a relativistic
is a relativisticTheory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
spin-1/2 field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
,
 is the Dirac spinor
is the Dirac spinorSpinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
related to a plane-wave with wave-vector
 ,
, ,
, is the four-wave-vector of the plane wave, where
is the four-wave-vector of the plane wave, where 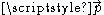 is arbitrary,
is arbitrary, are the four-coordinates in a given inertial frame of reference.
are the four-coordinates in a given inertial frame of reference.The Dirac spinor for the positive-frequency solution can be written as
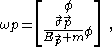
where
 is an arbitrary two-spinor,
is an arbitrary two-spinor,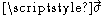 are the Pauli matrices
are the Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
,
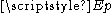 is the positive square root
is the positive square root 
Derivation from Dirac equation
The Dirac equation has the form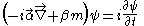
In order to derive the form of the four-spinor
 we have to first note the value of the matrices α and β:
we have to first note the value of the matrices α and β:
These two 4×4 matrices are related to the Dirac gamma matrices. Note that 0 and I are 2×2 matrices here.
The next step is to look for solutions of the form
 ,
,while at the same time splitting ω into two two-spinors:
 .
.Results
Using all of the above information to plug into the Dirac equation results in .
.This matrix equation is really two coupled equations:
Solve the 2nd equation for
 and one obtains
and one obtains .
.Solve the 1st equation for
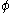 and one finds
and one finds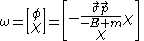 .
.This solution is useful for showing the relation between anti-particle and particle.
Two-spinors
The most convenient definitions for the two-spinors are: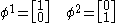
and

Pauli matrices
The Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
are

Using these, one can calculate:

Four-spinor for particles
Particles are defined as having positive energy. The normalization for the four-spinor ω is chosen so that . These spinors are denoted as u:
. These spinors are denoted as u: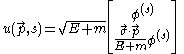
where s = 1 or 2 (spin "up" or "down")
Explicitly,

Four-spinor for anti-particles
Anti-particles having positive energy are defined as particles having negative energy and propagating backward in time. Hence changing the sign of
are defined as particles having negative energy and propagating backward in time. Hence changing the sign of  and
and  in the four-spinor for particles will give the four-spinor for anti-particles:
in the four-spinor for particles will give the four-spinor for anti-particles: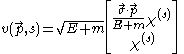
Here we choose the
 solutions. Explicitly,
solutions. Explicitly,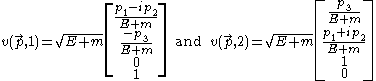
Completeness relations
The completeness relations for the four-spinors u and v are

where
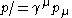 (see Feynman slash notation)
(see Feynman slash notation)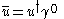
Dirac spinors and the Dirac algebra
The Dirac matrices are a set of four 4×4 matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
that are used as spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
and charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
operators
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
.
Conventions
There are several choices of signature and representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
that are in common use in the physics literature. The Dirac matrices are typically written as
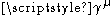 where
where  runs from 0 to 3. In this notation, 0 corresponds to time, and 1 through 3 correspond to x, y, and z.
runs from 0 to 3. In this notation, 0 corresponds to time, and 1 through 3 correspond to x, y, and z.The + − − − signature is sometimes called the west coast
West Coast of the United States
West Coast or Pacific Coast are terms for the westernmost coastal states of the United States. The term most often refers to the states of California, Oregon, and Washington. Although not part of the contiguous United States, Alaska and Hawaii do border the Pacific Ocean but can't be included in...
metric, while the − + + + is the east coast
East Coast of the United States
The East Coast of the United States, also known as the Eastern Seaboard, refers to the easternmost coastal states in the United States, which touch the Atlantic Ocean and stretch up to Canada. The term includes the U.S...
metric. At this time the + − − − signature is in more common use, and our example will use this signature. To switch from one example to the other, multiply all
 by
by  .
.After choosing the signature, there are many ways of constructing a representation in the 4×4 matrices, and many are in common use. In order to make this example as general as possible we will not specify a representation until the final step. At that time we will substitute in the "chiral"
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
or "Weyl"
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
representation as used in the popular graduate textbook An Introduction to Quantum Field Theory by Michael E. Peskin
Michael Peskin
Michael Peskin is an American theoretical physicist. He was an undergraduate at Harvard University and obtained his Ph.D. in 1978 at Cornell University studying under Kenneth Wilson. He was a Junior Fellow at the Harvard Society of Fellows from 1977–1980.He is currently a professor in the theory...
and Daniel V. Schroeder.
Construction
First we choose a spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
direction for our electron or positron. As with the example of the Pauli algebra discussed above, the spin direction is defined by a unit vector in 3 dimensions, (a, b, c). Following the convention of Peskin & Schroeder, the spin operator for spin in the (a, b, c) direction is defined as the dot product of (a, b, c) with the vector
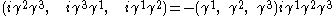

Note that the above is a root of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, that is, it squares to 1. Consequently, we can make a projection operator from it that projects out the sub-algebra of the Dirac algebra that has spin oriented in the (a, b, c) direction:
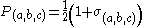
Now we must choose a charge, +1 (positron) or −1 (electron). Following the conventions of Peskin & Schroeder, the operator for charge is
 , that is, electron states will take an eigenvalue of −1 with respect to this operator while positron states will take an eigenvalue of +1.
, that is, electron states will take an eigenvalue of −1 with respect to this operator while positron states will take an eigenvalue of +1.Note that
 is also a square root of unity. Furthermore,
is also a square root of unity. Furthermore,  commutes with
commutes with  . They form a complete set of commuting operators for the Dirac algebra. Continuing with our example, we look for a representation of an electron with spin in the (a, b, c) direction. Turning
. They form a complete set of commuting operators for the Dirac algebra. Continuing with our example, we look for a representation of an electron with spin in the (a, b, c) direction. Turning  into a projection operator for charge = −1, we have
into a projection operator for charge = −1, we have
The projection operator for the spinor we seek is therefore the product of the two projection operators we've found:

The above projection operator, when applied to any spinor, will give that part of the spinor that corresponds to the electron state we seek. Therefore, to write down a 4×1 spinor we take any non zero column of the above matrix. Continuing the example, we put (a, b, c) = (0, 0, 1) and have

and so our desired projection operator is
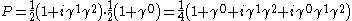
The 4×4 gamma matrices used in Peskin & Schroeder (Weyl representation) are
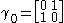
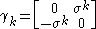
for k = 1, 2, 3 and where
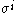 are the usual 2×2 Pauli matrices
are the usual 2×2 Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
. Substituting these in for P gives

Our answer is any non zero column of the above matrix. The division by two is just a normalization. The first and third columns give the same result:
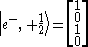
More generally, for electrons and positrons with spin oriented in the (a, b, c) direction, the projection operator is
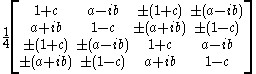
where the upper signs are for the electron and the lower signs are for the positron. The corresponding spinor can be taken as any non zero column. Since
 the different columns are multiples of the same spinor.
the different columns are multiples of the same spinor.