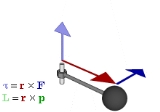
Torque
Encyclopedia
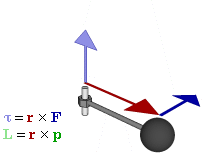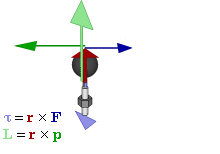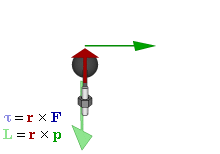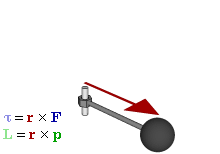
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
to rotate an object about an axis, fulcrum
Lever
In physics, a lever is a rigid object that is used with an appropriate fulcrum or pivot point to either multiply the mechanical force that can be applied to another object or resistance force , or multiply the distance and speed at which the opposite end of the rigid object travels.This leverage...
, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist.
Loosely speaking, torque is a measure of the turning force on an object such as a bolt or a flywheel
Flywheel
A flywheel is a rotating mechanical device that is used to store rotational energy. Flywheels have a significant moment of inertia, and thus resist changes in rotational speed. The amount of energy stored in a flywheel is proportional to the square of its rotational speed...
. For example, pushing or pulling the handle of a wrench connected to a nut or bolt produces a torque (turning force) that loosens or tightens the nut or bolt.
The symbol for torque is typically τ, the Greek letter
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
tau
Tau
Tau is the 19th letter of the Greek alphabet. In the system of Greek numerals it has a value of 300.The name in English is pronounced , but in modern Greek it is...
. When it is called moment, it is commonly denoted M.
The magnitude of torque depends on three quantities: the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
applied, the length of the lever arm connecting the axis to the point of force application, and the angle between the force vector and the lever arm. In symbols:
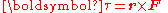

where
- τ is the torque vector and τ is the magnitude of the torque,
- r is the displacement vector (a vector from the point from which torque is measured to the point where force is applied), and r is the length (or magnitude) of the lever arm vector,
- F is the force vector, and F is the magnitude of the force,
- × denotes the cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, - θ is the angle between the force vector and the lever arm vector.
The length of the lever arm is particularly important; choosing this length appropriately lies behind the operation of lever
Lever
In physics, a lever is a rigid object that is used with an appropriate fulcrum or pivot point to either multiply the mechanical force that can be applied to another object or resistance force , or multiply the distance and speed at which the opposite end of the rigid object travels.This leverage...
s, pulley
Pulley
A pulley, also called a sheave or a drum, is a mechanism composed of a wheel on an axle or shaft that may have a groove between two flanges around its circumference. A rope, cable, belt, or chain usually runs over the wheel and inside the groove, if present...
s, gear
Gear
A gear is a rotating machine part having cut teeth, or cogs, which mesh with another toothed part in order to transmit torque. Two or more gears working in tandem are called a transmission and can produce a mechanical advantage through a gear ratio and thus may be considered a simple machine....
s, and most other simple machine
Simple machine
A simple machine is a mechanical device that changes the direction or magnitude of a force.In general, they can be defined as the simplest mechanisms that use mechanical advantage to multiply force. A simple machine uses a single applied force to do work against a single load force...
s involving a mechanical advantage
Mechanical advantage
Mechanical advantage is a measure of the force amplification achieved by using a tool, mechanical device or machine system. Ideally, the device preserves the input power and simply trades off forces against movement to obtain a desired amplification in the output force...
.
The SI unit for torque is the newton metre
Newton metre
A newton metre is a unit of torque in the SI system. The symbolic form is N m or N·m, and sometimes hyphenated newton-metre...
(N·m). For more on the units of torque, see below.
Terminology
This article follows US physics terminology by using the word torque. In the UK and in US mechanical engineeringMechanical engineering
Mechanical engineering is a discipline of engineering that applies the principles of physics and materials science for analysis, design, manufacturing, and maintenance of mechanical systems. It is the branch of engineering that involves the production and usage of heat and mechanical power for the...
, this is called moment.
In US Mechanical Engineering, the term torque means 'the resultant moment of a Couple
Couple (mechanics)
In mechanics, a couple is a system of forces with a resultant moment but no resultant force. Another term for a couple is a pure moment. Its effect is to create rotation without translation, or more generally without any acceleration of the centre of mass.The resultant moment of a couple is called...
', and (unlike in US physics), the terms torque and moment are not interchangeable. Torque is defined mathematically as the rate of change of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
of an object. The definition of torque states that one or both of the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
or the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
of an object are changing. And moment is the general term used for the tendency of one or more applied force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s to rotate an object about an axis, but not necessarily to change the angular momentum of the object (the concept which in physics is called torque).
For example, a rotational force applied to a shaft causing acceleration, such as a drill bit accelerating from rest, the resulting moment is called a torque. By contrast, a lateral force on a beam produces a moment (called a bending moment
Bending Moment
A bending moment exists in a structural element when a moment is applied to the element so that the element bends. Moments and torques are measured as a force multiplied by a distance so they have as unit newton-metres , or pound-foot or foot-pound...
), but since the angular momentum of the beam is not changing, this bending moment is not called a torque. Similarly with any force couple on an object that has no change to its angular momentum, such moment is also not called a torque.
This article follows the US physics terminology by calling all moments by the term torque, whether or not they cause the angular momentum of an object to change.
History
The concept of torque, also called momentMoment (physics)
In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...
or couple
Couple (mechanics)
In mechanics, a couple is a system of forces with a resultant moment but no resultant force. Another term for a couple is a pure moment. Its effect is to create rotation without translation, or more generally without any acceleration of the centre of mass.The resultant moment of a couple is called...
, originated with the studies of Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
on lever
Lever
In physics, a lever is a rigid object that is used with an appropriate fulcrum or pivot point to either multiply the mechanical force that can be applied to another object or resistance force , or multiply the distance and speed at which the opposite end of the rigid object travels.This leverage...
s. The rotational analogues of force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, and acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
are torque, moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
and angular acceleration
Angular acceleration
Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...
, respectively.
Definition and relation to angular momentum
Torque is defined about a point not specifically about axis as mentioned in several books.A force applied at a right angle to a lever multiplied by its distance from the lever's fulcrum
Lever
In physics, a lever is a rigid object that is used with an appropriate fulcrum or pivot point to either multiply the mechanical force that can be applied to another object or resistance force , or multiply the distance and speed at which the opposite end of the rigid object travels.This leverage...
(the length of the lever arm) is its torque. A force of three newtons applied two metre
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
s from the fulcrum, for example, exerts the same torque as a force of one newton applied six metres from the fulcrum. The direction of the torque can be determined by using the right hand grip rule: if the fingers of the right hand curl in the direction of rotation and the thumb points along the axis of rotation, then the thumb also points in the direction of the torque.
More generally, the torque on a particle (which has the position r in some reference frame) can be defined as the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
:
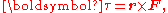
where r is the particle's position vector relative to the fulcrum, and F is the force acting on the particle. The magnitude τ of the torque is given by

where r is the distance from the axis of rotation to the particle, F is the magnitude of the force applied, and θ is the angle between the position and force vectors. Alternatively,
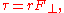
where F⊥ is the amount of force directed perpendicularly to the position of the particle. Any force directed parallel to the particle's position vector does not produce a torque.
It follows from the properties of the cross product that the torque vector is perpendicular to both the position and force vectors. It points along the axis of rotation, and its direction is determined by the right-hand rule.
The unbalanced torque on a body along axis of rotation determines the rate of change of the body's angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
,
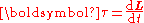
where L is the angular momentum vector and t is time. If multiple torques are acting on the body, it is instead the net torque which determines the rate of change of the angular momentum:
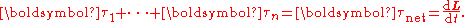
For rotation about a fixed axis,
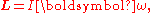
where I is the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
and ω is the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
. It follows that
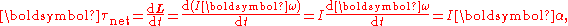
where α is the angular acceleration
Angular acceleration
Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...
of the body, measured in rad·s−2. This equation has the limitation that the torque equation is to be only written about instantaneous axis of rotation or center of mass for any type of motion - either motion is pure translation, pure rotation or mixed motion. I = Moment of inertia about point about which torque is written (either about instantaneous axis of rotation or center of mass only). If body is in translatory equilibrium then the torque equation is same about all points in the plane of motion.
Proof of the equivalence of definitions
The definition of angular momentum for a single particle is: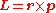
where "×" indicates the vector cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, p is the particle's linear momentum, and r is the displacement vector from the origin (the origin is assumed to be a fixed location anywhere in space). The time-derivative of this is:
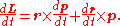
This result can easily be proven by splitting the vectors into components and applying the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
. Now using the definition of linear momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
p = mv (if mass is constant) and the definition of velocity
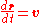
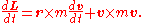
The cross product of any vector with itself is zero, so the second term vanishes. Hence with the definition of force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
(Newton's 2nd law),
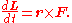
Then by definition, torque τ = r × F.
If multiple forces are applied, Newton's second law instead reads , and it follows that
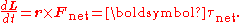
The proof relies on the assumption that mass is constant; this is valid only in non-relativistic systems in which no mass is being ejected.
Units
Torque has dimensions of force times distanceDistance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
. Official SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
literature suggests using the unit newton metre
Newton metre
A newton metre is a unit of torque in the SI system. The symbolic form is N m or N·m, and sometimes hyphenated newton-metre...
(N·m) or the unit joule
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
per radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
. The unit newton metre is properly denoted N·m or N m. This avoids ambiguity with mN, millinewtons.
The joule
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
, which is the SI unit for energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
or work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
, is dimensionally equivalent to a newton metre, but it is not used for torque. Energy and torque are entirely different concepts, so the practice of using different unit names for them helps avoid mistakes and misunderstandings. The dimensional equivalence of these units, of course, is not simply a coincidence: A torque of 1 N·m applied through a full revolution will require an energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
of exactly 2π joules. Mathematically,

where E is the energy, τ is magnitude of the torque, and θ is the angle moved (in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s). This equation motivates the alternate unit name joules per radian.
In British unit, "pound-force-feet
Pound-foot (torque)
A pound-foot is a unit of torque . One pound-foot is the torque created by one pound force acting at a perpendicular distance of one foot from a pivot point....
" (lbf x ft), "foot-pounds-force", "inch-pounds-force", "ounce-force-inch
Inch
An inch is the name of a unit of length in a number of different systems, including Imperial units, and United States customary units. There are 36 inches in a yard and 12 inches in a foot...
es" (oz x in) are used, and other non-SI units of torque includes "metre-kilograms-force
Kilogram-force
A kilogram-force , or kilopond , is a gravitational metric unit of force. It is equal to the magnitude of the force exerted by one kilogram of mass in a gravitational field...
". For all these units, the word "force" is often left out, for example abbreviating "pound-force-foot" to simply "pound-foot" (in this case, it would be implicit that the "pound" is pound-force
Pound-force
The pound force is a unit of force in some systems of measurement including English engineering units and British gravitational units.- Definitions :...
and not pound-mass).
Sometimes one may see torque given units that don't dimensionally make sense. For example: g x cm . In these units, g should be understood as the force given by the weight of 1 gram at the surface of the earth. The surface of the earth is understood to have an average acceleration of gravity (approx. 9.80665 m/sec2).
Moment arm formula
A very useful special case, often given as the definition of torque in fields other than physics, is as follows: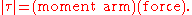
The construction of the "moment arm" is shown in the figure to the right, along with the vectors r and F mentioned above. The problem with this definition is that it does not give the direction of the torque but only the magnitude, and hence it is difficult to use in three-dimensional cases. If the force is perpendicular to the displacement vector r, the moment arm will be equal to the distance to the centre, and torque will be a maximum for the given force. The equation for the magnitude of a torque, arising from a perpendicular force:

For example, if a person places a force of 10 N on a spanner (wrench) which is 0.5 m long, the torque will be 5 N m, assuming that the person pulls the spanner by applying force perpendicular to the spanner.
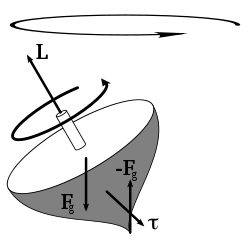
Static equilibrium
For an object to be in static equilibrium, not only must the sum of the forces be zero, but also the sum of the torques (moments) about any point. For a two-dimensional situation with horizontal and vertical forces, the sum of the forces requirement is two equations: ΣH = 0 and ΣV = 0, and the torque a third equation: Στ = 0. That is, to solve statically determinate equilibrium problems in two-dimensions, we use three equations.Net force versus torque
When the net force on the system is zero, the torque measured from any point in space is the same. For example, the torque on a current-carrying loop in a uniform magnetic field is the same regardless of your point of reference. If the net force is not zero, and
is not zero, and 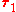 is the torque measured from
is the torque measured from 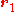 , then the torque measured from
, then the torque measured from 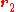 is
is
Machine torque
Torque is part of the basic specification of an engineEngine
An engine or motor is a machine designed to convert energy into useful mechanical motion. Heat engines, including internal combustion engines and external combustion engines burn a fuel to create heat which is then used to create motion...
: the power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
output of an engine is expressed as its torque multiplied by its rotational speed of the axis. Internal-combustion engines produce useful torque only over a limited range of rotational speeds (typically from around 1,000–6,000 rpm for a small car). The varying torque output over that range can be measured with a dynamometer
Dynamometer
A dynamometer or "dyno" for short, is a device for measuring force, moment of force , or power. For example, the power produced by an engine, motor or other rotating prime mover can be calculated by simultaneously measuring torque and rotational speed .A dynamometer can also be used to determine...
, and shown as a torque curve. The peak of that torque curve occurs somewhat below the overall power peak. The torque peak cannot, by definition, appear at higher rpm than the power peak.
Understanding the relationship between torque, power and engine speed is vital in automotive engineering
Automotive engineering
Modern automotive engineering, along with aerospace engineering and marine engineering, is a branch of vehicle engineering, incorporating elements of mechanical, electrical, electronic, software and safety engineering as applied to the design, manufacture and operation of motorcycles, automobiles,...
, concerned as it is with transmitting
Transmission (mechanics)
A machine consists of a power source and a power transmission system, which provides controlled application of the power. Merriam-Webster defines transmission as: an assembly of parts including the speed-changing gears and the propeller shaft by which the power is transmitted from an engine to a...
power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
from the engine through the drive train to the wheels. Power is a function of torque and engine speed. The gearing of the drive train must be chosen appropriately to make the most of the motor's torque characteristics. Power at the drive wheels is equal to engine power less mechanical losses regardless of any gearing between the engine and drive wheels.
Steam engine
Steam engine
A steam engine is a heat engine that performs mechanical work using steam as its working fluid.Steam engines are external combustion engines, where the working fluid is separate from the combustion products. Non-combustion heat sources such as solar power, nuclear power or geothermal energy may be...
s and electric motor
Electric motor
An electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
s tend to produce maximum torque close to zero rpm, with the torque diminishing as rotational speed rises (due to increasing friction and other constraints). Reciprocating steam engines can start heavy loads from zero RPM without a clutch
Clutch
A clutch is a mechanical device which provides for the transmission of power from one component to another...
.
Relationship between torque, power and energy
If a forceForce
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
is allowed to act through a distance, it is doing mechanical work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
. Similarly, if torque is allowed to act through a rotational distance, it is doing work. Mathematically, for rotation about a fixed axis through the center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
,
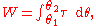
where W is work, τ is torque, and θ1 and θ2 represent (respectively) the initial and final angular positions of the body. It follows from the work-energy theorem that W also represents the change in the rotational kinetic energy
Rotational energy
The rotational energy or angular kinetic energy is the kinetic energy due to the rotation of an object and is part of its total kinetic energy...
Krot of the body, given by

where I is the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
of the body and ω is its angular speed.
Power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
is the work per unit time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, given by

where P is power, τ is torque, ω is the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
, and · represents the scalar product.
Mathematically, the equation may be rearranged to compute torque for a given power output. Note that the power injected by the torque depends only on the instantaneous angular speed – not on whether the angular speed increases, decreases, or remains constant while the torque is being applied (this is equivalent to the linear case where the power injected by a force depends only on the instantaneous speed – not on the resulting acceleration, if any).
In practice, this relationship can be observed in power stations which are connected to a large electrical power grid. In such an arrangement, the generator
Electrical generator
In electricity generation, an electric generator is a device that converts mechanical energy to electrical energy. A generator forces electric charge to flow through an external electrical circuit. It is analogous to a water pump, which causes water to flow...
's angular speed is fixed by the grid's frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
, and the power output of the plant is determined by the torque applied to the generator's axis of rotation.
Consistent units must be used. For metric SI units power is watt
Watt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s, torque is newton metre
Newton metre
A newton metre is a unit of torque in the SI system. The symbolic form is N m or N·m, and sometimes hyphenated newton-metre...
s and angular speed is radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s per second (not rpm and not revolutions per second).
Also, the unit newton metre is dimensionally equivalent
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
to the joule
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
, which is the unit of energy. However, in the case of torque, the unit is assigned to a vector, whereas for energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, it is assigned to a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
.
Conversion to other units
A conversion factor may be necessary when using different units of power, torque, or angular speed. For example, if rotational speedRotational speed
Rotational speed tells how many complete rotations there are per time unit. It is therefore a cyclic frequency, measured in hertz in the SI System...
(revolutions per time) is used in place of angular speed (radians per time), we multiply by a factor of 2π radians per revolution.

Adding units:
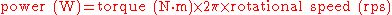
Dividing on the left by 60 seconds per minute and by 1000 watts per kilowatt gives us the following.

where rotational speed is in revolutions per minute (rpm).
Some people (e.g. American automotive engineers) use horsepower
Horsepower
Horsepower is the name of several units of measurement of power. The most common definitions equal between 735.5 and 750 watts.Horsepower was originally defined to compare the output of steam engines with the power of draft horses in continuous operation. The unit was widely adopted to measure the...
(imperial mechanical) for power, foot-pounds (lbf·ft) for torque and rpm for rotational speed. This results in the formula changing to:
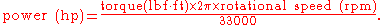
The constant below in, ft·lbf/min, changes with the definition of the horsepower; for example, using metric horsepower, it becomes ~32,550.
Use of other units (e.g. BTU/h for power) would require a different custom conversion factor.
Derivation
For a rotating object, the linear distance covered at the circumferenceCircumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
in a radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
of rotation is the product of the radius with the angular speed. That is: linear speed = radius × angular speed. By definition, linear distance=linear speed × time=radius × angular speed × time.
By the definition of torque: torque=force × radius. We can rearrange this to determine force=torque ÷ radius. These two values can be substituted into the definition of power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
:

The radius r and time t have dropped out of the equation. However angular speed must be in radians, by the assumed direct relationship between linear speed and angular speed at the beginning of the derivation. If the rotational speed is measured in revolutions per unit of time, the linear speed and distance are increased proportionately by 2π in the above derivation to give:

If torque is in lbf·ft and rotational speed in revolutions per minute, the above equation gives power in ft·lbf/min. The horsepower form of the equation is then derived by applying the conversion factor 33000 ft·lbf/min per horsepower:

because
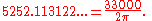
Principle of moments
The Principle of Moments, also known as Varignon's theorem (not to be confused with the geometrical theoremVarignon's theorem
Varignon's theorem is a statement in Euclidean geometry by Pierre Varignon that was first published in 1731. It deals with the construction of a particular parallelogram from an arbitrary quadrangle....
of the same name) states that the sum of torques due to several forces applied to a single point is equal to the torque due to the sum (resultant) of the forces. Mathematically, this follows from:

Torque multiplier
A torque multiplier is a gear box with reduction ratios greater than 1. The given torqueTorque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
at the input gets multiplied as per the reduction ratio and transmitted to the output, thereby achieving greater torque, but with reduced rotational speed.
External links
- Power and Torque Explained A clear explanation of the relationship between Power and Torque, and how they relate to engine performance.
- "Horsepower and Torque" An article showing how power, torque, and gearing affect a vehicle's performance.
- "Torque vs. Horsepower: Yet Another Argument" An automotive perspective
- a discussion of torque and angular momentum in an online textbook
- Torque and Angular Momentum in Circular Motion on Project PHYSNET.
- An interactive simulation of torque
- Torque Unit Converter
- Torque Measurement Primer
- Animation of how a bucking machine works

