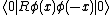Spin-statistics theorem
Encyclopedia
In quantum mechanics
, the spin-statistics theorem relates the spin
of a particle to the particle statistics
it obeys. The spin of a particle is its intrinsic angular momentum
(that is, the contribution to the total angular momentum which is not due to the orbital motion of the particle). All particles have either integer
spin or half-integer
spin (in units of the reduced Planck constant
ħ).
The theorem states that:
In other words, the spin-statistics theorem states that integer spin particles are bosons, while half-integer spin particles are fermions.
The spin-statistics relation was first formulated in 1939 by Markus Fierz
, and was rederived in a more systematic way by Wolfgang Pauli
. Fierz and Pauli argued by enumerating all free field theories, requiring that there should be quadratic forms for locally commuting observables including a positive definite energy density. A more conceptual argument was provided by Julian Schwinger
in 1950. Richard Feynman
gave a demonstration by demanding unitarity for scattering as an external potential is varied, which when translated to field language is a condition on the quadratic operator that couples to the potential.
A physical state is described by a wavefunction, or - more generally - by a vector, which is also called a "state"; if interactions with other particles are ignored, then two different wavefunctions are physically equivalent if their absolute value is equal. So,
while the physical state does not change under the exchange of the particles' positions, the wavefunction may get a minus sign.
Boson
s are particles whose wavefunction is symmetric under such an exchange, so if we swap the particles the wavefunction does not change. Fermion
s are particles whose wavefunction is antisymmetric, so under such a swap the wavefunction gets a minus sign. From this follows the Pauli exclusion principle
: two identical fermions cannot occupy the same state. This rule does not hold for bosons.
In quantum field theory, a state or a wavefunction is described by field operators operating on some basic state called the vacuum
. In order for the operators to project out the symmetric or antisymmetric component of the creating wavefunction, they must have the appropriate commutation law. The operator
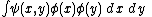
(with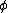
an operator and 
a numerical function)
creates a two-particle state with wavefunction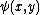
, and depending on the commutation properties of the fields, either only the antisymmetric parts or the symmetric parts matter.
Let us assume that
and the two operators take place at the same time; more generally, they may have spacelike separation, as is explained hereafter.
If the fields commute, meaning that the following holds
,
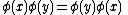then only the symmetric part of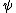
contributes, so that 
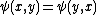and the field will create bosonic particles.
On the other hand if the fields anti-commute, meaning that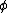
has the property that
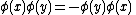
then only the antisymmetric part of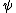
contributes, so that 
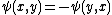, and the particles will be fermionic.
Naively, neither has anything to do with the spin, which determines the rotation properties of the particles, not the exchange properties.
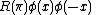
where R is the matrix which rotates the spin polarization of the field by 180 degrees when one does a 180 degree rotation around some particular axis. The components of phi are not shown in this notation,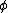
has many components, and the matrix R mixes them up with one another.
In a non-relativistic theory, this product can be interpreted as annihilating two particles at positions x and -x with polarizations which are rotated by π (180°) relative to each other. Now rotate this configuration by π around the origin. Under this rotation, the two points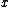
and 
switch places, and the two field polarizations are additionally rotated by a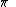 
. So you get
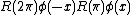
which for integer spin is equal to
and for half integer spin is equal to
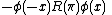
(proved here). Both the operators
still annihilate two particles at 
and 
. Hence we claim to have shown that, with respect to particle states: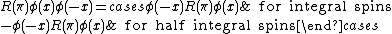 
.
So exchanging the order of two appropriately polarized operator insertions into the vacuum can be done by a rotation, at the cost of a sign in the half integer case.
This argument by itself does not prove anything like the spin/statistics relation. To see why, consider a nonrelativistic spin 0 field described by a free Schrödinger equation. Such a field can be anticommuting or commuting. To see where it fails, consider that a nonrelativistic spin 0 field has no polarization, so that the product above is simply:
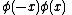
In the nonrelativistic theory, this product annihilates two particles at x and -x, and has zero expectation value in any state. In order to have a nonzero matrix element, this operator product must be between states with two more particles on the right than on the left:
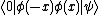
Performing the rotation, all that you learn is that rotating the 2-particle state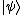
gives the same sign as changing the operator order. This is no information at all, so this argument does not prove anything.
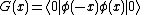
And now the heuristic argument can be used to see that G(x) is equal to G(-x), which tells you that the fields cannot be anti-commuting.
s. The field operators transform under Lorentz transformation
s according to the spin of the particle that they create, by definition.
Additionally, the assumption (known as microcausality
) that spacelike separated fields either commute or anticommute can be made only for relativistic theories with a time direction. Otherwise, the notion of being spacelike is meaningless. However, the proof involves looking at a Euclidean version of spacetime, in which the time direction is treated as a spatial one, as will be now explained.
Lorentz transformations include 3-dimensional rotations as well as boosts. A boost transfers to a frame of reference
with a different velocity, and is mathematically like a rotation into time. By analytic continuation
of the correlation functions of a quantum field theory, the time coordinate may become imaginary
, and then boosts become rotations. The new "spacetime" has only spatial directions, and is termed Euclidean.
A π rotation in the Euclidean x-t plane can be used to rotate vacuum expectation values of the field product of the previous section. The time rotation turns the argument of the previous section into the spin/statistics theorem.
The proof requires the following assumptions:
These assumptions are for the most part necessary, as the following examples show:
Assumptions 1 and 2 imply that the theory is described by a path integral, and assumption 3 implies that there is a local field which creates the particle.
The rotation plane includes time, and a rotation in a plane involving time in the Euclidean theory defines a CPT transformation in the Minkowski theory. If the theory is described by a path integral, a CPT transformation takes states to their conjugates, so that the correlation function
must be positive definite at x=0 by assumption 5, the particle states have positive norm. The assumption of finite mass implies that this correlation function is nonzero for x spacelike. Lorentz invariance now allows the fields to be rotated inside the correlation function in the manner of the argument of the previous section:
Where the sign depends on the spin, as before. The CPT invariance, or Euclidean rotational invariance, of the correlation function guarantees that this is equal to G(x). So
for integer spin fields and
for half-integer spin fields.
Since the operators are spacelike separated, a different order can only create states that differ by a phase. The argument fixes the phase to be -1 or 1 according to the spin. Since it is possible to rotate the space-like separated polarizations independently by local perturbations, the phase should not depend on the polarization in appropriately chosen field coordinates.
This argument is due to Julian Schwinger
.
, while integer-spin particles are not. Only one Fermion can occupy a given quantum state at any time, while the number of bosons that can occupy a quantum state is not restricted. The basic building blocks of matter such as proton
s, neutron
s, and electron
s are Fermions. Particles such as the photon
, which mediate forces between matter particles, are bosons.
There are a couple of interesting phenomena arising from the two types of statistics. The Bose-Einstein distribution which describes bosons leads to Bose-Einstein condensation. Below a certain temperature, most of the particles in a bosonic system will occupy the ground state (the state of lowest energy). Unusual properties such as superfluidity can result. The Fermi-Dirac distribution describing fermions also leads to interesting properties. Since only one fermion can occupy a given quantum state, the lowest single-particle energy level for spin-1/2 Fermions contains at most two particles, with the spins of the particles oppositely aligned. Thus, even at absolute zero
, the system still has a significant amount of energy. As a result, a fermionic system exerts an outward pressure
. Even at non-zero temperatures, such a pressure can exist. This degeneracy pressure is responsible for keeping certain massive stars from collapsing due to gravity. See white dwarf
, neutron star
, and black hole
.
Ghost fields do not obey the spin-statistics relation. See Klein transformation on how to patch up a loophole in the theorem.
has no non-trivial unitary representation
of finite dimension, it naively seems that one cannot construct a state with finite, non-zero spin and positive, Lorentz-invariant norm.
For a state of integer spin the negative norm states (known as "unphysical polarization") are set to zero, which makes the use of gauge symmetry necessary.
For a state of half-integer spin the argument can be circumvented by having fermionic statistics.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the spin-statistics theorem relates the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of a particle to the particle statistics
Particle statistics
Particle statistics refers to the particular description of particles in statistical mechanics.-Classical statistics:In classical mechanics all the particles in the system are considered distinguishable. This means that one can label and track each individual particle in a system...
it obeys. The spin of a particle is its intrinsic angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
(that is, the contribution to the total angular momentum which is not due to the orbital motion of the particle). All particles have either integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
spin or half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
spin (in units of the reduced Planck constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
ħ).
The theorem states that:
- the wave function of a system of identical integer-spin particles has the same value when the positions of any two particles are swapped. Particles with wavefunctions symmetric under exchange are called bosons;
- the wave function of a system of identical half-integer spin particles changes sign when two particles are swapped. Particles with wavefunctions anti-symmetric under exchange are called fermions.
In other words, the spin-statistics theorem states that integer spin particles are bosons, while half-integer spin particles are fermions.
The spin-statistics relation was first formulated in 1939 by Markus Fierz
Markus Fierz
Markus Eduard Fierz was a Swiss physicist, particularly remembered for his formulation of Spin-statistics theorem, and for his contributions to the development of quantum theory, particle physics, and statistical mechanics...
, and was rederived in a more systematic way by Wolfgang Pauli
Wolfgang Pauli
Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...
. Fierz and Pauli argued by enumerating all free field theories, requiring that there should be quadratic forms for locally commuting observables including a positive definite energy density. A more conceptual argument was provided by Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
in 1950. Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
gave a demonstration by demanding unitarity for scattering as an external potential is varied, which when translated to field language is a condition on the quadratic operator that couples to the potential.
General discussion
Two indistinguishable particles, occupying two separate points, have only one state, not two. This means that if we exchange the positions of the particles, we do not get a new state, but rather the same physical state. In fact, one cannot tell which particle is in which position.A physical state is described by a wavefunction, or - more generally - by a vector, which is also called a "state"; if interactions with other particles are ignored, then two different wavefunctions are physically equivalent if their absolute value is equal. So,
while the physical state does not change under the exchange of the particles' positions, the wavefunction may get a minus sign.
Boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s are particles whose wavefunction is symmetric under such an exchange, so if we swap the particles the wavefunction does not change. Fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s are particles whose wavefunction is antisymmetric, so under such a swap the wavefunction gets a minus sign. From this follows the Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
: two identical fermions cannot occupy the same state. This rule does not hold for bosons.
In quantum field theory, a state or a wavefunction is described by field operators operating on some basic state called the vacuum
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
. In order for the operators to project out the symmetric or antisymmetric component of the creating wavefunction, they must have the appropriate commutation law. The operator
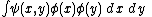
(with
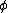an operator and a numerical function)creates a two-particle state with wavefunction
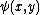, and depending on the commutation properties of the fields, either only the antisymmetric parts or the symmetric parts matter.Let us assume that
and the two operators take place at the same time; more generally, they may have spacelike separation, as is explained hereafter.If the fields commute, meaning that the following holds
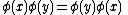,then only the symmetric part of
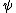contributes, so that 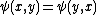and the field will create bosonic particles.On the other hand if the fields anti-commute, meaning that
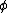has the property that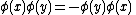then only the antisymmetric part of
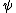contributes, so that 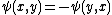, and the particles will be fermionic.Naively, neither has anything to do with the spin, which determines the rotation properties of the particles, not the exchange properties.
A suggestive bogus argument
Consider the two-field operator product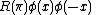where R is the matrix which rotates the spin polarization of the field by 180 degrees when one does a 180 degree rotation around some particular axis. The components of phi are not shown in this notation,
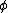has many components, and the matrix R mixes them up with one another.In a non-relativistic theory, this product can be interpreted as annihilating two particles at positions x and -x with polarizations which are rotated by π (180°) relative to each other. Now rotate this configuration by π around the origin. Under this rotation, the two points
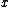and switch places, and the two field polarizations are additionally rotated by a 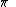. So you get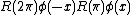which for integer spin is equal to
and for half integer spin is equal to
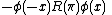
(proved here). Both the operators
still annihilate two particles at and . Hence we claim to have shown that, with respect to particle states: 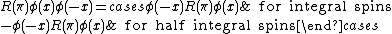.So exchanging the order of two appropriately polarized operator insertions into the vacuum can be done by a rotation, at the cost of a sign in the half integer case.
This argument by itself does not prove anything like the spin/statistics relation. To see why, consider a nonrelativistic spin 0 field described by a free Schrödinger equation. Such a field can be anticommuting or commuting. To see where it fails, consider that a nonrelativistic spin 0 field has no polarization, so that the product above is simply:
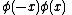
In the nonrelativistic theory, this product annihilates two particles at x and -x, and has zero expectation value in any state. In order to have a nonzero matrix element, this operator product must be between states with two more particles on the right than on the left:
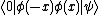
Performing the rotation, all that you learn is that rotating the 2-particle state
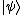gives the same sign as changing the operator order. This is no information at all, so this argument does not prove anything.Why the bogus argument fails
To prove spin/statistics, it is necessary to use relativity (though there are a few nice methods which do not use field theoretic tools). In relativity, there are no local fields which are pure creation operators or annihilation operators. Every local field both creates particles and annihilates the corresponding antiparticle. This means that in relativity, the product of the free real spin-0 field has a nonzero vacuum expectation value, because in addition to creating particles and annihilating particles, it also includes a part which creates and then annihilates a particle: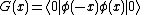And now the heuristic argument can be used to see that G(x) is equal to G(-x), which tells you that the fields cannot be anti-commuting.
Proof
The essential ingredient in proving the spin/statistics relation is relativity, that the physical laws do not change under Lorentz transformationLorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s. The field operators transform under Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s according to the spin of the particle that they create, by definition.
Additionally, the assumption (known as microcausality
Causality (physics)
Causality is the relationship between causes and effects. It is considered to be fundamental to all natural science, especially physics. Causality is also a topic studied from the perspectives of philosophy and statistics....
) that spacelike separated fields either commute or anticommute can be made only for relativistic theories with a time direction. Otherwise, the notion of being spacelike is meaningless. However, the proof involves looking at a Euclidean version of spacetime, in which the time direction is treated as a spatial one, as will be now explained.
Lorentz transformations include 3-dimensional rotations as well as boosts. A boost transfers to a frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
with a different velocity, and is mathematically like a rotation into time. By analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of the correlation functions of a quantum field theory, the time coordinate may become imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
, and then boosts become rotations. The new "spacetime" has only spatial directions, and is termed Euclidean.
A π rotation in the Euclidean x-t plane can be used to rotate vacuum expectation values of the field product of the previous section. The time rotation turns the argument of the previous section into the spin/statistics theorem.
The proof requires the following assumptions:
- The theory has a Lorentz invariant Lagrangian.
- The vacuum is Lorentz invariant.
- The particle is a localized excitation. Microscopically, it is not attached to a string or domain wall.
- The particle is propagating, meaning that it has a finite, not infinite, mass.
- The particle is a real excitation, meaning that states containing this particle have a positive definite norm.
These assumptions are for the most part necessary, as the following examples show:
- The spinless anticommuting fieldSchrödinger fieldIn quantum mechanics and quantum field theory, a Schrödinger field, named after Erwin Schrödinger, is a quantum field which obeys the Schrödinger equation...
shows that spinless fermions are nonrelativistically consistent. Likewise, the theory of a spinor commuting field shows that spinning bosons are too. - This assumption may be weakened.
- In 2+1 dimensions, sources for the Chern-Simons theoryChern-Simons theoryThe Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
can have exotic spins, despite the fact that the three dimensional rotation group has only integer and half-integer spin representations. - An ultralocal field can have either statistics independently of its spin. This is related to Lorentz invariance, since an infinitely massive particle is always nonrelativistic, and the spin decouples from the dynamics. Although colored quarks are attached to a QCD string and have infinite mass, the spin-statistics relation for quarks can be proved in the short distance limit.
- Gauge ghosts are spinless Fermions, but they include states of negative norm.
Assumptions 1 and 2 imply that the theory is described by a path integral, and assumption 3 implies that there is a local field which creates the particle.
The rotation plane includes time, and a rotation in a plane involving time in the Euclidean theory defines a CPT transformation in the Minkowski theory. If the theory is described by a path integral, a CPT transformation takes states to their conjugates, so that the correlation function
must be positive definite at x=0 by assumption 5, the particle states have positive norm. The assumption of finite mass implies that this correlation function is nonzero for x spacelike. Lorentz invariance now allows the fields to be rotated inside the correlation function in the manner of the argument of the previous section:
Where the sign depends on the spin, as before. The CPT invariance, or Euclidean rotational invariance, of the correlation function guarantees that this is equal to G(x). So
for integer spin fields and
for half-integer spin fields.
Since the operators are spacelike separated, a different order can only create states that differ by a phase. The argument fixes the phase to be -1 or 1 according to the spin. Since it is possible to rotate the space-like separated polarizations independently by local perturbations, the phase should not depend on the polarization in appropriately chosen field coordinates.
This argument is due to Julian Schwinger
Julian Schwinger
Julian Seymour Schwinger was an American theoretical physicist. He is best known for his work on the theory of quantum electrodynamics, in particular for developing a relativistically invariant perturbation theory, and for renormalizing QED to one loop order.Schwinger is recognized as one of the...
.
Consequences
Spin statistics theorem implies that half-integer spin particles are subject to the Pauli exclusion principlePauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
, while integer-spin particles are not. Only one Fermion can occupy a given quantum state at any time, while the number of bosons that can occupy a quantum state is not restricted. The basic building blocks of matter such as proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s, neutron
Neutron
The neutron is a subatomic hadron particle which has the symbol or , no net electric charge and a mass slightly larger than that of a proton. With the exception of hydrogen, nuclei of atoms consist of protons and neutrons, which are therefore collectively referred to as nucleons. The number of...
s, and electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s are Fermions. Particles such as the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
, which mediate forces between matter particles, are bosons.
There are a couple of interesting phenomena arising from the two types of statistics. The Bose-Einstein distribution which describes bosons leads to Bose-Einstein condensation. Below a certain temperature, most of the particles in a bosonic system will occupy the ground state (the state of lowest energy). Unusual properties such as superfluidity can result. The Fermi-Dirac distribution describing fermions also leads to interesting properties. Since only one fermion can occupy a given quantum state, the lowest single-particle energy level for spin-1/2 Fermions contains at most two particles, with the spins of the particles oppositely aligned. Thus, even at absolute zero
Absolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
, the system still has a significant amount of energy. As a result, a fermionic system exerts an outward pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
. Even at non-zero temperatures, such a pressure can exist. This degeneracy pressure is responsible for keeping certain massive stars from collapsing due to gravity. See white dwarf
White dwarf
A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...
, neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
, and black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
.
Ghost fields do not obey the spin-statistics relation. See Klein transformation on how to patch up a loophole in the theorem.
Relation to Representation theory of the Lorentz group
Since the Lorentz groupLorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
has no non-trivial unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of finite dimension, it naively seems that one cannot construct a state with finite, non-zero spin and positive, Lorentz-invariant norm.
For a state of integer spin the negative norm states (known as "unphysical polarization") are set to zero, which makes the use of gauge symmetry necessary.
For a state of half-integer spin the argument can be circumvented by having fermionic statistics.
Literature
- Markus Fierz: Über die relativistische Theorie kräftefreier Teilchen mit beliebigem Spin. Helv. Phys. Acta 12, 3-17 (1939)
- Wolfgang Pauli: The connection between spin and statistics. Phys. Rev. 58, 716-722 (1940)
- Ray F. Streater and Arthur S. Wightman: PCT, Spin & Statistics, and All That. 5th edition: Princeton University Press, Princeton (2000)
- Ian Duck and Ennackel Chandy George Sudarshan: Pauli and the Spin-Statistics Theorem. World Scientific, Singapore (1997)
- Arthur S Wightman: Pauli and the Spin-Statistics Theorem (book review). Am. J. Phys. 67 (8), 742-746 (1999)
- Arthur Jabs: Connecting spin and statistics in quantum mechanics. http://arXiv.org/abs/0810.2399 (Found. Phys. 40, 776-792, 793-794 (2010))
External links
- A nice nearly-proof at John Baez's home page
- parastatisticsParastatisticsIn quantum mechanics and statistical mechanics, parastatistics is one of several alternatives to the better known particle statistics models...
, anyonic statistics and braid statisticsBraid statisticsIn mathematics and theoretical physics, braid statistics is a generalization of the statistics of bosons and fermions based on the concept of braid group. A similar notion exists using a loop braid group.-See also:* Braid symmetry* Parastatistics...