
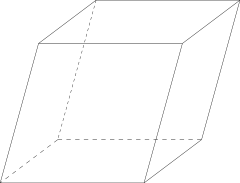
Parallelepiped
Encyclopedia
| Parallelepiped | |
|---|---|
 |
|
| Type | Prism Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... |
| Faces | 6 parallelogram Parallelogram In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure... s |
| Edges | 12 |
| Vertices | 8 |
| Symmetry group | Ci Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry... , [2+,2+], (1×) |
| Properties | convex |
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a parallelepiped is a three-dimensional figure formed by six parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
s. (The term rhomboid
Rhomboid
Traditionally, in two-dimensional geometry, a rhomboid is a parallelogram in which adjacent sides are of unequal lengths and angles are oblique.A parallelogram with sides of equal length is a rhombus but not a rhomboid....
is also sometimes used with this meaning.) By analogy, it relates to a parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
just as a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
relates to a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
. In Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, its definition encompasses all four concepts (i.e., parallelepiped, parallelogram, cube, and square). In this context of affine geometry
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
, in which angles are not differentiated, its definition admits only parallelograms and parallelepipeds. Three equivalent definitions of parallelepiped are
- a polyhedronPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with six faces (hexahedronHexahedronA hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....
), each of which is a parallelogram, - a hexahedron with three pairs of parallel faces, and
- a prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
of which the base is a parallelogramParallelogramIn Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
.
The rectangular cuboid
Cuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
(six rectangular faces), cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
(six square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
faces), and the rhombohedron
Rhombohedron
In geometry, a rhombohedron is a three-dimensional figure like a cube, except that its faces are not squares but rhombi. It is a special case of a parallelepiped where all edges are the same length....
(six rhombus
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
faces) are all specific cases of parallelepiped.
"Parallelepiped" is now usually icon, ˌ, or -; traditionally it was ˌ in accordance with its etymology in Greek
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
παραλληλ-επίπεδον, a body "having parallel planes".
Parallelepipeds are a subclass of the prismatoid
Prismatoid
In geometry, a prismatoid is a polyhedron where all vertices lie in two parallel planes....
s.
Properties
Any of the three pairs of parallel faces can be viewed as the base planes of the prism. A parallelepiped has three sets of four parallel edges; the edges within each set are of equal length.Parallelepipeds result from linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
(for the non-degenerate cases: the bijective linear transformations).
Since each face has point symmetry, a parallelepiped is a zonohedron
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
. Also the whole parallelepiped has point symmetry Ci (see also triclinic). Each face is, seen from the outside, the mirror image of the opposite face. The faces are in general chiral
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
, but the parallelepiped is not.
A space-filling tessellation
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
is possible with congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
copies of any parallelepiped.
Volume
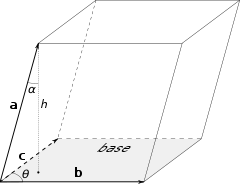
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a parallelepiped is the product of the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of its base A and its height h. The base is any of the six faces of the parallelepiped. The height is the perpendicular distance between the base and the opposite face.
An alternative method defines the vectors a = (a1, a2, a3), b = (b1, b2, b3) and c = (c1, c2, c3) to represent three edges that meet at one vertex. The volume of the parallelepiped then equals the absolute value of the scalar triple product a · (b × c):
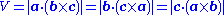
This is true because, if we choose b and c to represent the edges of the base, the area of the base is, by definition of the cross product (see geometric meaning of cross product),
- A = |b| |c| sin θ = |b × c|,
where θ is the angle between b and c, and the height is
- h = |a| cos α,
where α is the internal angle
Internal angle
In geometry, an interior angle is an angle formed by two sides of a polygon that share an endpoint. For a simple, convex or concave polygon, this angle will be an angle on the 'inner side' of the polygon...
between a and h.
From the figure, we can deduce that the magnitude of α is limited to 0° ≤ α < 90°. On the contrary, the vector b × c may form with a an internal angle β larger than 90° (0° ≤ β ≤ 180°). Namely, since b × c is parallel to h, the value of β is either β = α or β = 180° − α. So
- cos α = ±cos β = |cos β|,
and
- h = |a| |cos β|.
We conclude that
- V = Ah = |a| |b × c| |cos β|,
which is, by definition of the scalar product, equivalent to the absolute value of a · (b × c), Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...
.
The latter expression is also equivalent to the absolute value of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a three dimensional matrix built using a, b and c as rows (or columns):
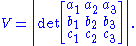
This is found using Cramer's Rule
Cramer's rule
In linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
on three reduced two dimensional matrices found from the original.
If a, b, and c are the parallelepiped edge lengths, and α, β, and γ are the internal angles between the edges, the volume is

Corresponding tetrahedron
The volume of any tetrahedronTetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
that shares three converging edges of a parallelepiped has a volume equal to one sixth of the volume of that parallelepiped (see proof).
Special cases
For parallelepipeds with a symmetry plane there are two cases:- it has four rectangular faces
- it has two rhombic faces, while of the other faces, two adjacent ones are equal and the other two also (the two pairs are each other's mirror image).
See also monoclinic.
A cuboid
Cuboid
In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
, also called a rectangular parallelepiped, is a parallelepiped of which all faces are rectangular; a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
is a cuboid with square faces.
A rhombohedron
Rhombohedron
In geometry, a rhombohedron is a three-dimensional figure like a cube, except that its faces are not squares but rhombi. It is a special case of a parallelepiped where all edges are the same length....
is a parallelepiped with all rhombic
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
faces; a trigonal trapezohedron
Trigonal trapezohedron
In geometry, the trigonal trapezohedron or deltohedron is the first in an infinite series of face-uniform polyhedra which are dual to the antiprisms. It has six faces which are congruent rhombi....
is a rhombohedron with congruent rhombic
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
faces.
Parallelotope
Coxeter called the generalization of a parallelepiped in higher dimensions a parallelotope.Specifically in n-dimensional space it is called n-dimensional parallelotope, or simply n-parallelotope. Thus a parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
is a 2-parallelotope and a parallelepiped is a 3-parallelotope.
The diagonals of an n-parallelotope intersect at one point and are bisected by this point. Inversion in this point leaves the n-parallelotope unchanged. See also fixed points of isometry groups in Euclidean space
Fixed points of isometry groups in Euclidean space
A fixed point of an isometry group is a point that is a fixed point for every isometry in the group. For any isometry group in Euclidean space the set of fixed points is either empty or an affine space....
.
The edges radiating from one vertex of a k-parallelotope form a k-frame
K-frame
In linear algebra, a branch of mathematics, a k-frame is an ordered set of k linearly independent vectors in a space; thus k ≤ n, where n is the dimension of the vector space, and if k = n an n-frame is precisely an ordered basis.If the vectors are orthogonal, or orthonormal,...
of the vector space, and the parallelotope can be recovered from these vectors, by taking linear combinations of the vectors, with weights between 0 and 1.
The n-volume of an n-parallelotope embedded in
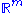 where
where  can be computed by means of the Gram determinant. Alternatively, the volume is the norm of the exterior product of the vectors:
can be computed by means of the Gram determinant. Alternatively, the volume is the norm of the exterior product of the vectors:
Lexicography
The word appears as parallelipipedon in Sir Henry Billingsley'sHenry Billingsley
Sir Henry Billingsley was Lord Mayor of London and the first translator of Euclid into English.-Early Life:He was a son of William Billingsley, haberdasher and assaymaster of London, and his wife, Elizabeth Harlowe. He entered St...
translation of Euclid's Elements
Euclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
, dated 1570. In the 1644 edition of his Cursus mathematicus, Pierre Hérigone
Pierre Hérigone
Pierre Hérigone was a French mathematician and astronomer.Of Basque origin, Hérigone taught in Paris for most of his life.-Works:...
used the spelling parallelepipedum. The OED cites the present-day parallelepiped as first appearing in Walter Charleton's
Walter Charleton
Walter Charleton was an English writer. According to Jon Parkin, he was "the main conduit for the transmission of Epicurean ideas to England".-Life:...
Chorea gigantum (1663).
Charles Hutton's
Charles Hutton
Charles Hutton was an English mathematician.Hutton was born at Newcastle-on-Tyne. He was educated in a school at Jesmond, kept by Mr Ivison, a clergyman of the Church of England...
Dictionary (1795) shows parallelopiped and parallelopipedon, showing the influence of the combining form parallelo-, as if the second element were pipedon rather than epipedon. Noah Webster
Noah Webster
Noah Webster was an American educator, lexicographer, textbook pioneer, English spelling reformer, political writer, editor, and prolific author...
(1806) includes the spelling parallelopiped. The 1989 edition of the Oxford English Dictionary
Oxford English Dictionary
The Oxford English Dictionary , published by the Oxford University Press, is the self-styled premier dictionary of the English language. Two fully bound print editions of the OED have been published under its current name, in 1928 and 1989. The first edition was published in twelve volumes , and...
describes parallelopiped (and parallelipiped) explicitly as incorrect forms, but these are listed without comment in the 2004 edition, and only pronunciations with the emphasis on the fifth syllable pi (/paɪ/) are given.
A change away from the traditional pronunciation has hidden the different partition suggested by the Greek roots, with epi- ("on") and pedon ("ground") combining to give epiped, a flat "plane". Thus the faces of a parallelepiped are planar, with opposite faces being parallel.

