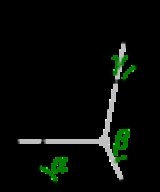
Crystal system
Encyclopedia
In crystallography
, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space group
s, lattices, point group
s, or crystal
s. Informally, two crystals tend to be in the same crystal system if they have similar symmetries, though there are many exceptions to this.
Crystal systems, crystal families, and lattice systems are similar but slightly different, and there is widespread confusion between them: in particular the trigonal crystal system is often confused with the rhombohedral lattice system, and the term "crystal system" is sometimes used to mean "lattice system" or "crystal family".
Space group
s and crystals are divided into 7 crystal systems according to their point group
s, and into 7 lattice systems according to their Bravais lattices. Five of the crystal systems are essentially the same as five of the lattice systems, but the hexagonal and trigonal crystal systems differ from the hexagonal and rhombohedral lattice systems.
The six crystal families are formed by combining the hexagonal and trigonal crystal systems into one hexagonal family, in order to eliminate this confusion.
A crystal system is a class of point groups. Two point groups are placed in the same crystal system if the sets of possible lattice systems of their space groups are the same. For many point groups there is only one possible lattice system,
and in these cases the crystal system corresponds to a lattice system and is given the same name. However, for the five point groups in the trigonal crystal class there are two possible lattice systems for their point groups: rhombohedral or hexagonal. In three dimensions there are seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic. The crystal system of a crystal or space group is determined by its point group but not always by its lattice.
A crystal family also consists of point groups and is formed by combining crystal systems whenever two crystal systems have space groups with the same lattice. In three dimensions a crystal family is almost the same as a crystal system (or lattice system), except that the hexagonal and trigonal crystal systems are combined into one hexagonal family. In three dimensions there are six crystal families: triclinic, monoclinic, orthorhombic, tetragonal, hexagonal, and cubic. The crystal family of a crystal or space group is determined by either its point group or its lattice, and crystal families are the smallest collections of point groups with this property.
In dimensions less than three there is no essential difference between crystal systems, crystal families, and lattice systems. There are 1 in dimension 0, 1 in dimension 1, and 4 in dimension 2, called oblique, rectangular, square, and hexagonal.
The relation between three-dimensional crystal families, crystal systems, and lattice systems is shown in the following table:
The crystal structure
s of biological molecules (such as protein
structures) can only occur in the 11 enantiomorphic
point groups, as biological molecules are invariably chiral
. The protein assemblies themselves may have symmetries other than those given above, because they are not intrinsically restricted by the Crystallographic restriction theorem
. For example the Rad52
DNA binding protein has an 11-fold rotational symmetry (in human), however, it must form crystals in one of the 11 enantiomorphic
point groups given above.
In geometry
and crystallography
, a Bravais lattice is a category of symmetry group
s for translational symmetry
in three directions, or correspondingly, a category of translation lattice
s.
Such symmetry groups consist of translations by vectors of the form

where n1, n2, and n3 are integer
s and a1, a2, and a3 are three non-coplanar vectors, called primitive vectors.
These lattices are classified by space group
of the translation lattice itself; there are 14 Bravais lattices in three dimensions; each can apply in one lattice system only. They represent the maximum symmetry a structure with the translational symmetry concerned can have.
All crystalline materials must, by definition fit in one of these arrangements (not including quasicrystal
s).
For convenience a Bravais lattice is depicted by a unit cell which is a factor 1, 2, 3 or 4 larger than the primitive cell
. Depending on the symmetry of a crystal or other pattern, the fundamental domain
is again smaller, up to a factor 48.
The Bravais lattices were studied by Moritz Ludwig Frankenheim (1801-1869), in 1842, who found that there were 15 Bravais lattices. This was corrected to 14 by A. Bravais
in 1848.
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s, lattices, point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
s, or crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s. Informally, two crystals tend to be in the same crystal system if they have similar symmetries, though there are many exceptions to this.
Crystal systems, crystal families, and lattice systems are similar but slightly different, and there is widespread confusion between them: in particular the trigonal crystal system is often confused with the rhombohedral lattice system, and the term "crystal system" is sometimes used to mean "lattice system" or "crystal family".
Space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s and crystals are divided into 7 crystal systems according to their point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
s, and into 7 lattice systems according to their Bravais lattices. Five of the crystal systems are essentially the same as five of the lattice systems, but the hexagonal and trigonal crystal systems differ from the hexagonal and rhombohedral lattice systems.
The six crystal families are formed by combining the hexagonal and trigonal crystal systems into one hexagonal family, in order to eliminate this confusion.
Overview
A lattice system is a class of lattices with the same point group. In three dimensions there are seven lattice systems: triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal, and cubic. The lattice system of a crystal or space group is determined by its lattice but not always by its point group.A crystal system is a class of point groups. Two point groups are placed in the same crystal system if the sets of possible lattice systems of their space groups are the same. For many point groups there is only one possible lattice system,
and in these cases the crystal system corresponds to a lattice system and is given the same name. However, for the five point groups in the trigonal crystal class there are two possible lattice systems for their point groups: rhombohedral or hexagonal. In three dimensions there are seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic. The crystal system of a crystal or space group is determined by its point group but not always by its lattice.
A crystal family also consists of point groups and is formed by combining crystal systems whenever two crystal systems have space groups with the same lattice. In three dimensions a crystal family is almost the same as a crystal system (or lattice system), except that the hexagonal and trigonal crystal systems are combined into one hexagonal family. In three dimensions there are six crystal families: triclinic, monoclinic, orthorhombic, tetragonal, hexagonal, and cubic. The crystal family of a crystal or space group is determined by either its point group or its lattice, and crystal families are the smallest collections of point groups with this property.
In dimensions less than three there is no essential difference between crystal systems, crystal families, and lattice systems. There are 1 in dimension 0, 1 in dimension 1, and 4 in dimension 2, called oblique, rectangular, square, and hexagonal.
The relation between three-dimensional crystal families, crystal systems, and lattice systems is shown in the following table:
| Crystal family | Crystal system | Required symmetries of point group | point groups Crystallographic point group In crystallography, a crystallographic point group is a set of symmetry operations, like rotations or reflections, that leave a central point fixed while moving other directions and faces of the crystal to the positions of features of the same kind... |
space group Space group In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct... s |
bravais lattices | Lattice system |
|---|---|---|---|---|---|---|
| Triclinic | None | 2 | 2 | 1 | Triclinic | |
| Monoclinic | 1 twofold axis of rotation Rotational symmetry Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has... or 1 mirror plane Reflection symmetry Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a... |
3 | 13 | 2 | Monoclinic | |
| Orthorhombic | 3 twofold axes of rotation or 1 twofold axis of rotation and two mirror planes. | 3 | 59 | 4 | Orthorhombic | |
| Tetragonal | 1 fourfold axis of rotation | 7 | 68 | 2 | Tetragonal | |
| Hexagonal | Trigonal | 1 threefold axis of rotation | 5 | 7 | 1 | Rhombohedral |
| 18 | 1 | Hexagonal | ||||
| Hexagonal Hexagonal crystal system In crystallography, the hexagonal crystal system is one of the 7 crystal systems, the hexagonal lattice system is one of the 7 lattice systems, and the hexagonal crystal family is one of the 6 crystal families... |
1 sixfold axis of rotation | 7 | 27 | |||
| Cubic Cubic crystal system In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals.... |
4 threefold axes of rotation | 5 | 36 | 3 | Cubic Cubic crystal system In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals.... |
|
| Total: 6 | 7 | 32 | 230 | 14 | 7 | |
Crystal systems
The distribution of the 32 point groups into the 7 crystal systems is given in the following table.| crystal family | crystal system | point group Point group In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O... / crystal class |
Schönflies | Hermann-Mauguin | Orbifold Orbifold In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold... |
Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M... |
Type | order Symmetry number The symmetry number or symmetry order of an object is the number of different but indistinguishable arrangements of the object, i.e. the order of its symmetry group... |
structure |
|---|---|---|---|---|---|---|---|---|---|
| triclinic Triclinic crystal system thumb|180px|Triclinic In crystallography, the triclinic crystal system is one of the 7 crystal systems. A crystal system is described by three basis vectors. In the triclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system... |
triclinic-pedial | C1 | 1 | 11 | [ ]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
1 | trivial | |
| triclinic-pinacoidal | Ci | 1x | [2,1+] | centrosymmetric | 2 | cyclic | |||
| monoclinic Monoclinic crystal system In crystallography, the monoclinic crystal system is one of the 7 lattice point groups. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. They form a rectangular prism with a... |
monoclinic-sphenoidal | C2 | 2 | 22 | [2,2]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
2 | cyclic | |
| monoclinic-domatic | Cs | m | *11 | [ ] | polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
2 | cyclic | ||
| monoclinic-prismatic Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... |
C2h | 2/m | 2* | [2,2+] | centrosymmetric | 4 | 2×cyclic | ||
| orthorhombic Orthorhombic crystal system In crystallography, the orthorhombic crystal system is one of the seven lattice point groups. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base and height , such that a,... |
orthorhombic-sphenoidal | D2 | 222 | 222 | [2,2]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... |
4 | dihedral | |
| orthorhombic-pyramidal Pyramid (geometry) In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base.... |
C2v | mm2 | *22 | [2] | polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
4 | dihedral | ||
| orthorhombic-bipyramid Bipyramid An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The... al |
D2h | mmm | *222 | [2,2] | centrosymmetric | 8 | 2×dihedral | ||
| tetragonal Tetragonal crystal system In crystallography, the tetragonal crystal system is one of the 7 lattice point groups. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base and height .There are two tetragonal Bravais... |
tetragonal-pyramidal | C4 | 4 | 44 | [4]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
4 | Cyclic | |
| tetragonal-disphenoidal | S4 | 2x | [2+,2] | 4 | cyclic | ||||
| tetragonal-dipyramidal | C4h | 4/m | 4* | [2,4+] | centrosymmetric | 8 | 2×cyclic | ||
| tetragonal-trapezoidal | D4 | 422 | 422 | [2,4]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... |
8 | dihedral | ||
| ditetragonal-pyramidal | C4v | 4mm | *44 | [4] | polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
8 | dihedral | ||
| tetragonal-scalenoidal | D2d | 2m or m2 | 2*2 | [2+,4] | 8 | dihedral | |||
| ditetragonal-dipyramidal | D4h | 4/mmm | *422 | [2,4] | centrosymmetric | 16 | 2×dihedral | ||
| hexagonal | trigonal | trigonal-pyramidal | C3 | 3 | 33 | [3]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
3 | cyclic |
| rhombohedral | S6 (C3i) | 3x | [2+,3+] | centrosymmetric | 6 | cyclic | |||
| trigonal-trapezoidal | D3 | 32 or 321 or 312 | 322 | [3,2]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... |
6 | dihedral | ||
| ditrigonal-pyramidal | C3v | 3m or 3m1 or 31m | *33 | [3] | polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
6 | dihedral | ||
| ditrigonal-scalahedral | D3d | m or m1 or 1m | 2*3 | [2+,6] | centrosymmetric | 12 | dihedral | ||
| hexagonal Hexagonal crystal system In crystallography, the hexagonal crystal system is one of the 7 crystal systems, the hexagonal lattice system is one of the 7 lattice systems, and the hexagonal crystal family is one of the 6 crystal families... |
hexagonal-pyramidal | C6 | 6 | 66 | [6]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
6 | cyclic | |
| trigonal-dipyramidal | C3h | 3* | [2,3+] | 6 | cyclic | ||||
| hexagonal-dipyramidal | C6h | 6/m | 6* | [2,6+] | centrosymmetric | 12 | 2×cyclic | ||
| hexagonal-trapezoidal | D6 | 622 | 622 | [2,6]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... |
12 | dihedral | ||
| dihexagonal-pyramidal | C6v | 6mm | *66 | [6] | polar Chemical polarity In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in... |
12 | dihedral | ||
| ditrigonal-dipyramidal | D3h | m2 or 2m | *322 | [2,3] | 12 | dihedral | |||
| dihexagonal-dipyramidal | D6h | 6/mmm | *622 | [2,6] | centrosymmetric | 24 | 2×dihedral | ||
| cubic Cubic crystal system In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals.... |
tetrahedral | T | 23 | 332 | [3,3]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... |
12 | Alternating | |
| tetrahedral | Td | 3m | *332 | [3,3] | 24 | symmetric | |||
| diploidal | Th | m | 3*2 | [3+,4] | centrosymmetric | 24 | 2×alternating | ||
| gyroidal | O | 432 | 432 | [4,3]+ | enantiomorphic Chirality (chemistry) A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom.... |
24 | symmetric | ||
| hexoctahedral | Oh | mm | *432 | [4,3] | centrosymmetric | 48 | 2×symmetric | ||
The crystal structure
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
s of biological molecules (such as protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
structures) can only occur in the 11 enantiomorphic
Chirality (chemistry)
A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom....
point groups, as biological molecules are invariably chiral
Chirality (chemistry)
A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom....
. The protein assemblies themselves may have symmetries other than those given above, because they are not intrinsically restricted by the Crystallographic restriction theorem
Crystallographic restriction theorem
The crystallographic restriction theorem in its basic form was based on the observation that the rotational symmetries of a crystal are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold...
. For example the Rad52
RAD52
RAD52 homolog , also known as RAD52, is a protein which in humans is encoded by the RAD52 gene.- Function :The protein encoded by this gene shares similarity with Saccharomyces cerevisiae Rad52, a protein important for DNA double-strand break repair and homologous recombination...
DNA binding protein has an 11-fold rotational symmetry (in human), however, it must form crystals in one of the 11 enantiomorphic
Chirality (chemistry)
A chiral molecule is a type of molecule that lacks an internal plane of symmetry and thus has a non-superimposable mirror image. The feature that is most often the cause of chirality in molecules is the presence of an asymmetric carbon atom....
point groups given above.
Lattice systems
The distribution of the 14 Bravais lattice types into 7 lattice systems is given in the following table.| The 7 lattice systems | The 14 Bravais Lattices | |||
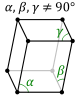
| triclinic Triclinic crystal system thumb|180px|Triclinic In crystallography, the triclinic crystal system is one of the 7 crystal systems. A crystal system is described by three basis vectors. In the triclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system... (parallelepiped Parallelepiped In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts... ) |
 |
|||
| monoclinic Monoclinic crystal system In crystallography, the monoclinic crystal system is one of the 7 lattice point groups. A crystal system is described by three vectors. In the monoclinic system, the crystal is described by vectors of unequal length, as in the orthorhombic system. They form a rectangular prism with a... (right prism Prism (geometry) In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a... with parallelogram Parallelogram In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure... base; here seen from above) |
simple | base-centered | ||
 |
 |
|||
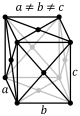
| orthorhombic Orthorhombic crystal system In crystallography, the orthorhombic crystal system is one of the seven lattice point groups. Orthorhombic lattices result from stretching a cubic lattice along two of its orthogonal pairs by two different factors, resulting in a rectangular prism with a rectangular base and height , such that a,... (cuboid Cuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... ) |
simple | base-centered | body-centered | face-centered |
 |
 |
 |
 |
|
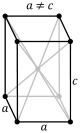
| tetragonal Tetragonal crystal system In crystallography, the tetragonal crystal system is one of the 7 lattice point groups. Tetragonal crystal lattices result from stretching a cubic lattice along one of its lattice vectors, so that the cube becomes a rectangular prism with a square base and height .There are two tetragonal Bravais... (square cuboid Cuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... ) |
simple | body-centered | ||
 |
 |
|||
| rhombohedral (trigonal trapezohedron Trigonal trapezohedron In geometry, the trigonal trapezohedron or deltohedron is the first in an infinite series of face-uniform polyhedra which are dual to the antiprisms. It has six faces which are congruent rhombi.... ) |
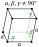 |
|||
| hexagonal Hexagonal crystal system In crystallography, the hexagonal crystal system is one of the 7 crystal systems, the hexagonal lattice system is one of the 7 lattice systems, and the hexagonal crystal family is one of the 6 crystal families... (centered regular hexagon) |
 |
|||
| cubic Cubic crystal system In crystallography, the cubic crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals.... (isometric; cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... ) |
simple | body-centered | face-centered | |
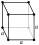 |
 |
 |
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
, a Bravais lattice is a category of symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s for translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
in three directions, or correspondingly, a category of translation lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
s.
Such symmetry groups consist of translations by vectors of the form

where n1, n2, and n3 are integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and a1, a2, and a3 are three non-coplanar vectors, called primitive vectors.
These lattices are classified by space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
of the translation lattice itself; there are 14 Bravais lattices in three dimensions; each can apply in one lattice system only. They represent the maximum symmetry a structure with the translational symmetry concerned can have.
All crystalline materials must, by definition fit in one of these arrangements (not including quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
s).
For convenience a Bravais lattice is depicted by a unit cell which is a factor 1, 2, 3 or 4 larger than the primitive cell
Primitive cell
Used predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions...
. Depending on the symmetry of a crystal or other pattern, the fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
is again smaller, up to a factor 48.
The Bravais lattices were studied by Moritz Ludwig Frankenheim (1801-1869), in 1842, who found that there were 15 Bravais lattices. This was corrected to 14 by A. Bravais
Auguste Bravais
Auguste Bravais was a French physicist, well known for his work in crystallography...
in 1848.
See also
- Crystal clusterCrystal clusterA crystal depending upon its chemical composition, bonding power, atmospheric pressure and ambient environment form clusters. A crystal cluster is the development of a crystal system and is also known as a crystal family. Though crystal family as a technical term in crystallography is a matrix of...
- Crystal structureCrystal structureIn mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
- List of the 230 crystallographic 3D space groups
External links
- Overview of the 32 groups
- Mineral galleries - Symmetry
- all cubic crystal classes, forms and stereographic projections (interactive java applet)
- Crystal system at the Online Dictionary of Crystallography
- Crystal family at the Online Dictionary of Crystallography
- Lattice system at the Online Dictionary of Crystallography
- Conversion Primitive to Standard Conventional for VASP input files
- Learning Crystallography

