Lattice problems
Encyclopedia
In computer science
, lattice problems are a class of optimization problems on lattices
. The conjectured intractability of such problems is central to construction of secure lattice-based cryptosystems. For applications in such cryptosystems, lattices over vector spaces (often
) or free modules (often 
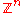) are generally considered.
For all the problems below, assume that we are given (in addition to other more specific inputs) a basis for the vector space V and a norm
N. The norms usually considered are L2. However, other norms (such as Lp) are also considered and show up in variety of results. Let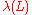
denote the length of the shortest non-zero vector in the lattice L: 
.
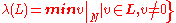of a vector space
V and a norm
N (often L2) are given for a lattice L and one must find the shortest non-zero vector in V, as measured by N, in L. In other words, the algorithm should output a non-zero vector v such that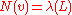
.
In the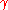
-approximation version 
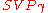, one must find a non-zero lattice vector of length at most 
.
.
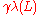Approach techniques: Lenstra–Lenstra–Lovász lattice basis reduction algorithm
produces a "relatively short vector" in polynomial time, but does not solve the problem.
Kannan's HKZ basis reduction algorithm solves the problem in
time where n is the dimension.
Lastly, Schnorr presented a technique that interpolates between LLL and HKZ called Block Reduction. Block reduction works with HKZ bases and if the number of blocks is chosen to be larger than the dimension, the resulting algorithm Kannan's full HKZ basis reduction.
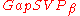consists of differentiating between the instances of SVP in which the answer is at most 1 or larger than 
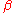, where 
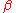can be a fixed function of 
, the number of vectors. Given a basis for the lattice, the algorithm must decide whether 
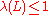or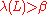 
. Like other promise problem
s, the algorithm is allowed to err on all other cases.
Yet another version of the problem is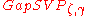
for some functions 
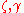. The input to the algorithm is a basis 
and a number 
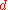. It is assured that all the vectors in the Gram–Schmidt orthogonalization are of length at least 1, and that 
and that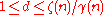 
where 
is the dimension. The algorithm must accept if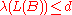 
, and reject if 
. For large 
(
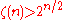), the problem is equivalent to 
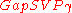because a preprocessing done using the LLL algorithm makes the second condition (and hence, 
) redundant.
M (often L2
) are given for a lattice L, as well as a vector v in V but not necessarily in L. It is desired to find the vector in L closest to v (as measured by M). In the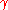
-approximation version 
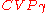, one must find a lattice vector at distance at most 
.
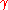(defined below), one can solve 
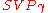by making some queries to the oracle. The naive method to find the shortest vector by calling the 
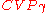oracle to find the closest vector to 0 does not work because 0 is itself a lattice vector and the algorithm could potentially output 0.
The reduction from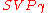
to 
is as follows: Suppose that the input to the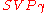 
problem is the basis for lattice 
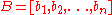. Consider the basis 
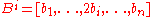and let 
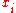be the vector returned by 
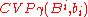. The claim is that the shortest vector in the set 
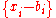is the shortest vector in the given lattice.
unless 
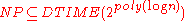. Dinur et al. strengthened this by giving a NP-hardness result with 
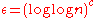for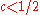 
.
) wireless communication systems (for coded and uncoded signals).
The Fincke-Pohst algorithm was applied in the field of the integer ambiguity resolution of carrier-phase GNSS (GPS).
, the input consists of a lattice basis and a vector 
and the algorithm must answer whether
for any approximation factor.
Schnorr, in 1987, showed that deterministic polynomial time algorithms can solve the problem for
. Ajtai et al. showed that probabilistic algorithms can achieve a slightly better approximation factor of 
In 1993, Banaszczyk showed that
is in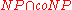 
. In 2000, Goldreich and Goldwasser showed that 
puts the problem in both NP and coAM. In 2005, Ahoronov and Regev showed that for some constant 
, the problem with 
is in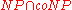 
.
For lower bounds, Dinur et al. showed in 1998 that the problem is NP-hard for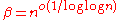
.
so that 
where the right hand side considers all basis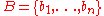 
of the lattice.
In the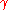
-approximate version, given a lattice L with dimension n, find n linearly independent vectors 
of length max ||
|| ≤ 
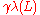
, the algorithm must output the closest lattice vector to it.
, output an equivalent basis 
such that the length of the longest vector in 
is as short as possible.
The approximation version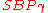
problem consist of finding a basis whose longest vector is at most 
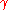times longer than the longest vector in the shortest basis.
The above lattice problems are easy to solve if the algorithm is provided with a "good" basis. Lattice reduction
algorithms aim, given a basis for a lattice, to output a new basis consisting of relatively short, nearly orthogonal vectors. The LLL algorithm was an early efficient algorithm for this problem which could output a almost reduced lattice basis in polynomial time. This algorithm and its further refinements were used to break several cryptographic schemes, establishing its status as a very important tool in cryptanalysis. The success of LLL on experimental data led to a belief that lattice reduction might be an easy problem in practice. However, this belief was challenged when in the late 1990s, several new results on the hardness of lattice problems were obtained, starting with the result of Ajtai.
In his seminal papers, Ajtai showed that the SVP problem was NP-hard and discovered some connections between the worst-case complexity and average-case complexity
of some lattice problems. Building on these results, Ajtai and Dwork created a public-key cryptosystem whose security could be proven using only the worst case hardness of a certain version of SVP, thus making it the first result to have used worst-case hardness to create secure systems.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, lattice problems are a class of optimization problems on lattices
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
. The conjectured intractability of such problems is central to construction of secure lattice-based cryptosystems. For applications in such cryptosystems, lattices over vector spaces (often
) or free modules (often 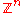) are generally considered.For all the problems below, assume that we are given (in addition to other more specific inputs) a basis for the vector space V and a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
N. The norms usually considered are L2. However, other norms (such as Lp) are also considered and show up in variety of results. Let
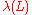denote the length of the shortest non-zero vector in the lattice L: 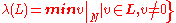.Shortest vector problem (SVP)
In SVP, a basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V and a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
N (often L2) are given for a lattice L and one must find the shortest non-zero vector in V, as measured by N, in L. In other words, the algorithm should output a non-zero vector v such that
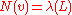.In the
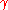-approximation version 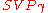, one must find a non-zero lattice vector of length at most 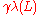.Known results
The exact version of the problem is NP-hardNP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
.
Approach techniques: Lenstra–Lenstra–Lovász lattice basis reduction algorithm
Lenstra–Lenstra–Lovász lattice basis reduction algorithm
The LLL-reduction algorithm is a polynomial time lattice reduction algorithm invented by Arjen Lenstra, Hendrik Lenstra and László Lovász in 1982, see...
produces a "relatively short vector" in polynomial time, but does not solve the problem.
Kannan's HKZ basis reduction algorithm solves the problem in
time where n is the dimension.Lastly, Schnorr presented a technique that interpolates between LLL and HKZ called Block Reduction. Block reduction works with HKZ bases and if the number of blocks is chosen to be larger than the dimension, the resulting algorithm Kannan's full HKZ basis reduction.
GapSVP
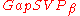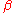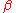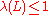The problem consists of differentiating between the instances of SVP in which the answer is at most 1 or larger than , where can be a fixed function of , the number of vectors. Given a basis for the lattice, the algorithm must decide whether or 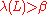. Like other promise problemPromise problem
In computational complexity theory, a promise problem is a generalization of a decision problem where the input is promised to belong to a subset of all possible inputs. Unlike decision problems, the yes instances and no instances do not exhaust the set of all inputs...
s, the algorithm is allowed to err on all other cases.
Yet another version of the problem is
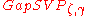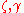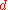for some functions . The input to the algorithm is a basis and a number . It is assured that all the vectors in the Gram–Schmidt orthogonalization are of length at least 1, and that and that 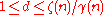where is the dimension. The algorithm must accept if 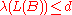, and reject if . For large (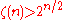), the problem is equivalent to 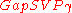because a preprocessing done using the LLL algorithm makes the second condition (and hence, ) redundant.Closest vector problem (CVP)
In CVP, a basis of a vector space V and a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
M (often L2
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
) are given for a lattice L, as well as a vector v in V but not necessarily in L. It is desired to find the vector in L closest to v (as measured by M). In the
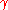-approximation version 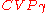, one must find a lattice vector at distance at most 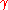.Relationship with SVP
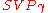It is a more general case of the shortest vector problem. It is easy to show that given an oracle for (defined below), one can solve by making some queries to the oracle. The naive method to find the shortest vector by calling the 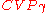oracle to find the closest vector to 0 does not work because 0 is itself a lattice vector and the algorithm could potentially output 0.The reduction from
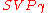to is as follows: Suppose that the input to the 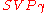problem is the basis for lattice 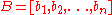. Consider the basis 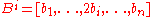and let 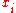be the vector returned by 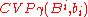. The claim is that the shortest vector in the set 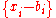is the shortest vector in the given lattice.Known results
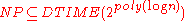Goldreich et al. showed that any hardness of SVP implies the same hardness for CVP. Using PCP tools, Arora et al. showed that CVP is hard to approximate within factor unless . Dinur et al. strengthened this by giving a NP-hardness result with 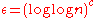for 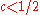.Sphere decoding
The algorithm for CVP, especially the Fincke and Pohst variant, have been used, for example, for data detection in multiple-input multiple-output (MIMOMIMO
In radio, multiple-input and multiple-output, or MIMO , is the use of multiple antennas at both the transmitter and receiver to improve communication performance. It is one of several forms of smart antenna technology...
) wireless communication systems (for coded and uncoded signals).
The Fincke-Pohst algorithm was applied in the field of the integer ambiguity resolution of carrier-phase GNSS (GPS).
GapCVP
This problem is similar to the GapSVP problem. For, the input consists of a lattice basis and a vector and the algorithm must answer whether
- there is a lattice vector such that the distance between it and
is at most 1. - every lattice vector is at a distance greater than
away from 
.
Known results
The problem is trivially contained in NPNP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
for any approximation factor.
Schnorr, in 1987, showed that deterministic polynomial time algorithms can solve the problem for
. Ajtai et al. showed that probabilistic algorithms can achieve a slightly better approximation factor of In 1993, Banaszczyk showed that
is in 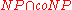. In 2000, Goldreich and Goldwasser showed that puts the problem in both NP and coAM. In 2005, Ahoronov and Regev showed that for some constant , the problem with is in 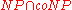.For lower bounds, Dinur et al. showed in 1998 that the problem is NP-hard for
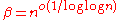.Shortest independent vector problem (SIVP)
Given a lattice L of dimension n, the algorithm must output n linearly independent so that where the right hand side considers all basis 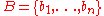of the lattice.In the
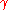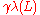
-approximate version, given a lattice L with dimension n, find n linearly independent vectors of length max |||| ≤ Bounded distance decoding
This problem is similar to CVP. Given a vector such that its distance from the lattice is at most, the algorithm must output the closest lattice vector to it.Covering radius problem
Given a basis for the lattice, the algorithm must find the largest distance (or in some versions, its approximation) from any vector to the lattice.Shortest basis problem
Many problems become easier if the input basis consists of short vectors. An algorithm that solves the Shortest Basis Problem (SBP) must, given an lattice basis, output an equivalent basis such that the length of the longest vector in is as short as possible.The approximation version
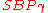problem consist of finding a basis whose longest vector is at most 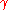times longer than the longest vector in the shortest basis.Use in cryptography
Average case hardness of problems forms a basis for proofs-of-security for most cryptographic schemes. However, experimental evidence suggests that most NP-hard problems lack this property: they are probably only worst case hard. Many lattice problems have been conjectured or proven to be average-case hard, making them an attractive class of problems to base cryptographic schemes on. Moreover, worst-case hardness of some lattice problems have been used to create secure cryptographic schemes. The use of worst-case hardness in such schemes makes them among the very few schemes that are very likely secure even against Quantum computers.The above lattice problems are easy to solve if the algorithm is provided with a "good" basis. Lattice reduction
Lattice reduction
In mathematics, the goal of lattice basis reduction is given an integer lattice basis as input, to find a basis with short, nearly orthogonal vectors. This is realized using different algorithms, whose running time is usually at least exponential in the dimension of the lattice.-Nearly...
algorithms aim, given a basis for a lattice, to output a new basis consisting of relatively short, nearly orthogonal vectors. The LLL algorithm was an early efficient algorithm for this problem which could output a almost reduced lattice basis in polynomial time. This algorithm and its further refinements were used to break several cryptographic schemes, establishing its status as a very important tool in cryptanalysis. The success of LLL on experimental data led to a belief that lattice reduction might be an easy problem in practice. However, this belief was challenged when in the late 1990s, several new results on the hardness of lattice problems were obtained, starting with the result of Ajtai.
In his seminal papers, Ajtai showed that the SVP problem was NP-hard and discovered some connections between the worst-case complexity and average-case complexity
Average-case complexity
Average-case complexity is a subfield of computational complexity theory that studies the complexity of algorithms on random inputs.The study of average-case complexity has applications in the theory of cryptography....
of some lattice problems. Building on these results, Ajtai and Dwork created a public-key cryptosystem whose security could be proven using only the worst case hardness of a certain version of SVP, thus making it the first result to have used worst-case hardness to create secure systems.