Crystallographic restriction theorem
Encyclopedia
The crystallographic restriction theorem in its basic form was based on the observation that the rotation
al symmetries
of a crystal
are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold. However, quasicrystal
s can occur with other symmetries, such as 5-fold; these were not discovered until 1982, when a diffraction pattern out off a quasicrystal
was first seen by the Israeli scientist Dan Shectman, who won the 2011 Nobel Prize in Chemistry
for his discovery.
Prior to the discovery of quasicrystals, crystals were modeled as discrete lattice
s, generated by a list of independent
finite translation
s . Because discreteness requires that the spacings between lattice points have a lower bound, the group
of rotational symmetries of the lattice at any point must be a finite group
. The strength of the theorem is that not all finite groups are compatible with a discrete lattice; in any dimension, we will have only a finite number of compatible groups.
s) and 3D (space group
s) are most heavily used in applications, and we can treat them together.
of coplanar lattice points. We now confine our attention to the plane in which the symmetry acts . (We might call this a proof in the style of Busby Berkeley
, with lattice vectors rather than pretty ladies dancing and swirling in geometric patterns.)
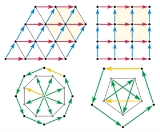
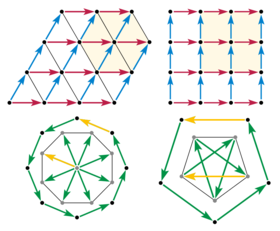 Now consider an 8-fold rotation, and the displacement vectors between adjacent points of the polygon. If a displacement exists between any two lattice points, then that same displacement is repeated everywhere in the lattice. So collect all the edge displacements to begin at a single lattice point. The edge vectors become radial vectors, and their 8-fold symmetry implies a regular octagon of lattice points around the collection point. But this is impossible, because the new octagon is about 80% smaller than the original. The significance of the shrinking is that it is unlimited. The same construction can be repeated with the new octagon, and again and again until the distance between lattice points is as small as we like; thus no discrete lattice can have 8-fold symmetry. The same argument applies to any k-fold rotation, for k greater than 6.
Now consider an 8-fold rotation, and the displacement vectors between adjacent points of the polygon. If a displacement exists between any two lattice points, then that same displacement is repeated everywhere in the lattice. So collect all the edge displacements to begin at a single lattice point. The edge vectors become radial vectors, and their 8-fold symmetry implies a regular octagon of lattice points around the collection point. But this is impossible, because the new octagon is about 80% smaller than the original. The significance of the shrinking is that it is unlimited. The same construction can be repeated with the new octagon, and again and again until the distance between lattice points is as small as we like; thus no discrete lattice can have 8-fold symmetry. The same argument applies to any k-fold rotation, for k greater than 6.
A shrinking argument also eliminates 5-fold symmetry. Consider a regular pentagon of lattice points. If it exists, then we can take every other edge displacement and (head-to-tail) assemble a 5-point star, with the last edge returning to the starting point. The vertices of such a star are again vertices of a regular pentagon with 5-fold symmetry, but about 60% smaller than the original.
Thus the theorem is proved.
The existence of quasicrystals and Penrose tiling
s shows that the assumption of a linear translation is necessary. Penrose tilings may have 5-fold rotational symmetry and a discrete lattice, and any local neighborhood of the tiling is repeated infinitely many times, but there is no linear translation for the tiling as a whole. And without the discrete lattice assumption, the above construction not only fails to reach a contradiction, but produces a (non-discrete) counterexample. Thus 5-fold rotational symmetry cannot be eliminated by an argument missing either of those assumptions. A Penrose tiling of the whole (infinite) plane can only have exact 5-fold rotational symmetry (of the whole tiling) about a single point, however, whereas the 4-fold and 6-fold lattices have infinitely many centres of rotational symmetry.
r = mr
The four translation vectors (three of which are given by r, and one which connects A' and B' given by r') form a parallelogram. Therefore, the length of r' is also given by:
r = -2rcos(α) + r
Combining the two equations gives:
cos(α) = (1 - m)/2 = M/2
Where M = 1-m is also an integer. Since we always have:
| cos(α) | ≤ 1
it follows that:
| M | ≤ 2
It can be shown that the only values of α in the 0° to 180° range that satisfy the three equations above are 0°, 60°, 90°, 120°, and 180°. In terms of radians, the only allowed rotations consistent with lattice periodicity are given by 2π/n, where n = 1, 2, 3, 4, 6. This corresponds to 1-, 2-, 3-, 4-, and 6-fold symmetry, respectively, and therefore excludes the possibility of 5-fold or greater than 6-fold symmetry.
(See also the sketch in section Preuve mathématique simple of the French Wikipedia article (Théorème de restriction cristallographique)
properties. The sum of the diagonal elements of a matrix is called the trace of the matrix. In 2D and 3D every rotation is a planar rotation, and the trace is a function of the angle alone. For a 2D rotation, the trace is 2 cos θ; for a 3D rotation, 1 + 2 cos θ.
Examples
Using a lattice basis, neither orthogonality nor unit length is guaranteed, only independence. However, the trace is the same with respect to any basis. (Similarity transforms preserve trace.) In a lattice basis, because the rotation must map lattice points to lattice points, each matrix entry — and hence the trace — must be an integer. Thus, for example, wallpaper and crystals cannot have 8-fold rotational symmetry. The only possibilities are multiples of 60°, 90°, 120°, and 180°, corresponding to 6-, 4-, 3-, and 2-fold rotations.
Example
The general crystallographic restriction on rotations does not guarantee that a rotation will be compatible with a specific lattice. For example, a 60° rotation will not work with a square lattice; nor will a 90° rotation work with a rectangular lattice.
. This is of interest, not just for mathematics, but for the physics of quasicrystals under the cut-and-project theory. In this view, a 3D quasicrystal with 8-fold rotation symmetry might be described as the projection of a slab cut from a 4D lattice.
The following 4D rotation matrix is the aforementioned eightfold symmetry of the hypercube
(and the cross-polytope
):
Transforming this matrix to the new coordinates given by will produce:
will produce:
This third matrix then corresponds to a rotation both by 45° (in the first two dimensions) and by 135° (in the last two). Projecting a slab of hypercubes along the first two dimensions of the new coordinates produces an Ammann–Beenker tiling
(another such tiling is produced by projecting along the last two dimensions), which therefore also has 8-fold rotational symmetry on average.
The A4 lattice and F4 lattice have order 10 and order 12 rotational symmetries, respectively.
To state the restriction for all dimensions, it is convenient to shift attention away from rotations alone and concentrate on the integer matrices . We say that a matrix A has order
k when its k-th power (but no lower), Ak, equals the identity. Thus a 6-fold rotation matrix in the equilateral triangle basis is an integer matrix with order 6. Let OrdN denote the set of integers that can be the order of an N×N integer matrix. For example, Ord2 = {1, 2, 3, 4, 6}. We wish to state an explicit formula for OrdN.
Define a function ψ based on Euler's totient function
φ; it will map positive integers to non-negative integers. For an odd prime
, p, and a positive integer, k, set ψ(pk) equal to the totient function value,
φ(pk), which in this case is pk−pk−1. Do the same for ψ(2k) when k > 1. Set ψ(2) and ψ(1) to 0. Using the fundamental theorem of arithmetic
, we can write any other positive integer uniquely as a product of prime powers, m = ∏α pαk α; set ψ(m) = ∑α ψ(pαk α). This differs from the totient itself, because it is a sum instead of a product.
The crystallographic restriction in general form states that OrdN consists of those positive integers m such that ψ(m) ≤ N.
Note that these additional symmetries do not allow a planar slice to have, say, 8-fold rotation symmetry. In the plane, the 2D restrictions still apply. Thus the cuts used to model quasicrystals necessarily have thickness.
Integer matrices are not limited to rotations; for example, a reflection is also a symmetry of order 2. But by insisting on determinant +1, we can restrict the matrices to proper rotations.
of Euclidean space
. A set of isometries can form a group
. By a discrete isometry group we will mean an isometry group that maps every point to a discrete subset of RN, i.e. a set of isolated point
s. With this terminology, the crystallographic restriction theorem in two and three dimensions can be formulated as follows.
Note that isometries of order n include, but are not restricted to, n-fold rotations. The theorem also excludes S8, S12, D4d, and D6d (see point groups in three dimensions
), even though they have 4- and 6-fold rotational symmetry only.
Note also that rotational symmetry of any order about an axis is compatible with translational symmetry along that axis.
The result in the table above implies that for every discrete isometry group in four- and five-dimensional space which includes translations spanning the whole space, all isometries of finite order are of order 1, 2, 3, 4, 5, 6, 8, 10, or 12.
All isometries of finite order in six- and seven-dimensional space are of order 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 24 or 30 .
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
al symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of a crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
are usually limited to 2-fold, 3-fold, 4-fold, and 6-fold. However, quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
s can occur with other symmetries, such as 5-fold; these were not discovered until 1982, when a diffraction pattern out off a quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
was first seen by the Israeli scientist Dan Shectman, who won the 2011 Nobel Prize in Chemistry
Nobel Prize in Chemistry
The Nobel Prize in Chemistry is awarded annually by the Royal Swedish Academy of Sciences to scientists in the various fields of chemistry. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895, awarded for outstanding contributions in chemistry, physics, literature,...
for his discovery.
Prior to the discovery of quasicrystals, crystals were modeled as discrete lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
s, generated by a list of independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
finite translation
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
s . Because discreteness requires that the spacings between lattice points have a lower bound, the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of rotational symmetries of the lattice at any point must be a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
. The strength of the theorem is that not all finite groups are compatible with a discrete lattice; in any dimension, we will have only a finite number of compatible groups.
Dimensions 2 and 3
The special cases of 2D (wallpaper groupWallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s) and 3D (space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s) are most heavily used in applications, and we can treat them together.
Lattice proof
A rotation symmetry in dimension 2 or 3 must move a lattice point to a succession of other lattice points in the same plane, generating a regular polygonRegular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
of coplanar lattice points. We now confine our attention to the plane in which the symmetry acts . (We might call this a proof in the style of Busby Berkeley
Busby Berkeley
Busby Berkeley was a highly influential Hollywood movie director and musical choreographer. Berkeley was famous for his elaborate musical production numbers that often involved complex geometric patterns...
, with lattice vectors rather than pretty ladies dancing and swirling in geometric patterns.)

A shrinking argument also eliminates 5-fold symmetry. Consider a regular pentagon of lattice points. If it exists, then we can take every other edge displacement and (head-to-tail) assemble a 5-point star, with the last edge returning to the starting point. The vertices of such a star are again vertices of a regular pentagon with 5-fold symmetry, but about 60% smaller than the original.
Thus the theorem is proved.
The existence of quasicrystals and Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
s shows that the assumption of a linear translation is necessary. Penrose tilings may have 5-fold rotational symmetry and a discrete lattice, and any local neighborhood of the tiling is repeated infinitely many times, but there is no linear translation for the tiling as a whole. And without the discrete lattice assumption, the above construction not only fails to reach a contradiction, but produces a (non-discrete) counterexample. Thus 5-fold rotational symmetry cannot be eliminated by an argument missing either of those assumptions. A Penrose tiling of the whole (infinite) plane can only have exact 5-fold rotational symmetry (of the whole tiling) about a single point, however, whereas the 4-fold and 6-fold lattices have infinitely many centres of rotational symmetry.
Trigonometry proof
Consider two lattice points A and B separated by a translation vector r. Consider an angle α such that a rotation of angle α about any lattice point is a symmetry of the lattice. Rotating about point B by α maps point A to a new point A'. Similarly, rotating about point A by α, in the opposite direction, maps B to a point B'. Since both rotations mentioned are symmetry operations, A' and B' must both be lattice points. Due to periodicity of the crystal, the new vector r' which connects them must be equal to an integral multiple of r:r = mr
The four translation vectors (three of which are given by r, and one which connects A' and B' given by r') form a parallelogram. Therefore, the length of r' is also given by:
r = -2rcos(α) + r
Combining the two equations gives:
cos(α) = (1 - m)/2 = M/2
Where M = 1-m is also an integer. Since we always have:
| cos(α) | ≤ 1
it follows that:
| M | ≤ 2
It can be shown that the only values of α in the 0° to 180° range that satisfy the three equations above are 0°, 60°, 90°, 120°, and 180°. In terms of radians, the only allowed rotations consistent with lattice periodicity are given by 2π/n, where n = 1, 2, 3, 4, 6. This corresponds to 1-, 2-, 3-, 4-, and 6-fold symmetry, respectively, and therefore excludes the possibility of 5-fold or greater than 6-fold symmetry.
Short trigonometry proof
Consider a line of atoms A-O-B, separated by distance t. Rotate the entire row by +2π/n and -2π/n, with point O kept fixed. Due to the assumed periodicity of the lattice, the two lattice points C and D will be also in a directly below the initial row; moreover C and D will be separated by r = mt, with m an integer. But by the geometry, the separation between these points is 2tcos(2π/n). Equating the two relations gives 2cos(2π/n) = m. This is satisfied by only n = 1, 2, 3, 4, 6.(See also the sketch in section Preuve mathématique simple of the French Wikipedia article (Théorème de restriction cristallographique)
Matrix proof
For an alternative proof, consider matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
properties. The sum of the diagonal elements of a matrix is called the trace of the matrix. In 2D and 3D every rotation is a planar rotation, and the trace is a function of the angle alone. For a 2D rotation, the trace is 2 cos θ; for a 3D rotation, 1 + 2 cos θ.
Examples
- Consider a 60° (6-fold) rotation matrix with respect to an orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
in 2D.
-
- The trace is precisely 1, an integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
.- Consider a 45° (8-fold) rotation matrix.
- The trace is 2/√2, not an integer.
Using a lattice basis, neither orthogonality nor unit length is guaranteed, only independence. However, the trace is the same with respect to any basis. (Similarity transforms preserve trace.) In a lattice basis, because the rotation must map lattice points to lattice points, each matrix entry — and hence the trace — must be an integer. Thus, for example, wallpaper and crystals cannot have 8-fold rotational symmetry. The only possibilities are multiples of 60°, 90°, 120°, and 180°, corresponding to 6-, 4-, 3-, and 2-fold rotations.
Example
- Consider a 60° (360°/6) rotation matrix with respect to the obliqueObliqueOblique may refer to:*Oblique angle, in geometry, an angle that is not a multiple of 90 degrees*Oblique angle, synonym for Dutch angle, a cinematographic technique*Oblique , by jazz vibraphonist Bobby Hutcherson...
lattice basis for a tilingTessellationA tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
by equilateral triangles.
-
- The trace is still 1. The determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
(always +1 for a rotation) is also preserved.
The general crystallographic restriction on rotations does not guarantee that a rotation will be compatible with a specific lattice. For example, a 60° rotation will not work with a square lattice; nor will a 90° rotation work with a rectangular lattice.
Higher dimensions
When the dimension of the lattice rises to four or more, rotations need no longer be planar; the 2D proof is inadequate. However, restrictions still apply, though more symmetries are permissible. For example, the hypercubic lattice has an eightfold rotational symmetry, corresponding to an eightfold rotational symmetry of the hypercubeHypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
. This is of interest, not just for mathematics, but for the physics of quasicrystals under the cut-and-project theory. In this view, a 3D quasicrystal with 8-fold rotation symmetry might be described as the projection of a slab cut from a 4D lattice.
The following 4D rotation matrix is the aforementioned eightfold symmetry of the hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
(and the cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
):

Transforming this matrix to the new coordinates given by
 will produce:
will produce:
This third matrix then corresponds to a rotation both by 45° (in the first two dimensions) and by 135° (in the last two). Projecting a slab of hypercubes along the first two dimensions of the new coordinates produces an Ammann–Beenker tiling
Ammann–Beenker tiling
In geometry, an Ammann–Beenker tiling is a nonperiodic tiling generated by an aperiodic set of prototiles named after Robert Ammann, who first discovered the tilings in the 1970s, and after F. P. M...
(another such tiling is produced by projecting along the last two dimensions), which therefore also has 8-fold rotational symmetry on average.
The A4 lattice and F4 lattice have order 10 and order 12 rotational symmetries, respectively.
To state the restriction for all dimensions, it is convenient to shift attention away from rotations alone and concentrate on the integer matrices . We say that a matrix A has order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
k when its k-th power (but no lower), Ak, equals the identity. Thus a 6-fold rotation matrix in the equilateral triangle basis is an integer matrix with order 6. Let OrdN denote the set of integers that can be the order of an N×N integer matrix. For example, Ord2 = {1, 2, 3, 4, 6}. We wish to state an explicit formula for OrdN.
Define a function ψ based on Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
φ; it will map positive integers to non-negative integers. For an odd prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, p, and a positive integer, k, set ψ(pk) equal to the totient function value,
φ(pk), which in this case is pk−pk−1. Do the same for ψ(2k) when k > 1. Set ψ(2) and ψ(1) to 0. Using the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
, we can write any other positive integer uniquely as a product of prime powers, m = ∏α pαk α; set ψ(m) = ∑α ψ(pαk α). This differs from the totient itself, because it is a sum instead of a product.
The crystallographic restriction in general form states that OrdN consists of those positive integers m such that ψ(m) ≤ N.
| m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| ψ(m) | 0 | 0 | 2 | 2 | 4 | 2 | 6 | 4 | 6 | 4 | 10 | 4 | 12 | 6 | 6 | 8 | 16 | 6 | 18 | 6 | 8 | 10 | 22 | 6 | 20 | 12 | 18 | 8 | 28 | 6 | 30 |
Note that these additional symmetries do not allow a planar slice to have, say, 8-fold rotation symmetry. In the plane, the 2D restrictions still apply. Thus the cuts used to model quasicrystals necessarily have thickness.
Integer matrices are not limited to rotations; for example, a reflection is also a symmetry of order 2. But by insisting on determinant +1, we can restrict the matrices to proper rotations.
Formulation in terms of isometries
The crystallographic restriction theorem can be formulated in terms of isometriesIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. A set of isometries can form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. By a discrete isometry group we will mean an isometry group that maps every point to a discrete subset of RN, i.e. a set of isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s. With this terminology, the crystallographic restriction theorem in two and three dimensions can be formulated as follows.
- For every discrete isometry groupIsometry groupIn mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
in two- and three-dimensional space which includes translations spanning the whole space, all isometries of finite orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
are of order 1, 2, 3, 4 or 6.
Note that isometries of order n include, but are not restricted to, n-fold rotations. The theorem also excludes S8, S12, D4d, and D6d (see point groups in three dimensions
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
), even though they have 4- and 6-fold rotational symmetry only.
Note also that rotational symmetry of any order about an axis is compatible with translational symmetry along that axis.
The result in the table above implies that for every discrete isometry group in four- and five-dimensional space which includes translations spanning the whole space, all isometries of finite order are of order 1, 2, 3, 4, 5, 6, 8, 10, or 12.
All isometries of finite order in six- and seven-dimensional space are of order 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 24 or 30 .




