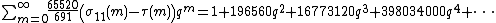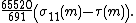Leech lattice
Encyclopedia
In mathematics
, the Leech lattice is an even unimodular lattice
Λ24 in 24-dimensional Euclidean space
E24 found by .
calculated the order of the automorphism group of the Leech lattice, and discovered three new sporadic group
s as a by-product: the Conway groups, Co1, Co2, Co3.
, has a single rather cryptic sentence mentioning that he found more than 10 even unimodular lattices in 24 dimensions without giving further details.
In a seminar in 1970 Ernst Witt
claimed that one of the lattices he found in 1940 was the Leech lattice. See his collected works for more comments and for some notes Witt wrote about this in 1972.
, hexagonal tiling and E8 lattice
, respectively.
It has no root system
and in fact is the first unimodular lattice
with no roots (vectors of norm less than 4), and therefore has a centre density of 1. By multiplying this value by the volume of a unit ball in 24 dimensions,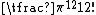
, one can derive its absolute density.
showed that the Leech lattice is isometric to the set of simple roots (or the Dynkin diagram) of the reflection group
of the 26-dimensional even Lorentzian unimodular lattice II25,1. By comparison, the Dynkin diagrams of II9,1 and II17,1 are finite.
, a 24×24 matrix with determinant
1.
and for each fixed residue class modulo 4, the 24 bit word, whose 1's correspond to the coordinates i such that ai belongs to this residue class, is a word in the binary Golay code
. The Golay code, together with the related Witt Design, features in a construction for the 196560 minimal vectors in the Leech lattice.
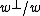where w is the Weyl vector:
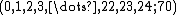
in the 26-dimensional even Lorentzian unimodular lattice
II25,1
. The existence of such an integral vector of norm zero relies on the fact that 12 + 22 + ... + 242 is a perfect square
(in fact 702); the number 24 is the only integer bigger than 1 with this property. This was conjectured by Édouard Lucas
, but the proof came much later, based on elliptic functions.
The vector
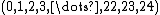
in this construction is really the Weyl vector of the even sublattice D24 of the odd unimodular lattice I25. More generally, if L is any positive definite unimodular lattice of dimension 25 with at least 4 vectors of norm 1, then the Weyl vector of its norm 2 roots has integral length, and there is a similar construction of the Leech lattice using L and this Weyl vector.
. It can also be constructed by using three copies of the E8 lattice
, in the same way that the binary Golay code can be constructed using three copies of the extended Hamming code
, H8. This construction is known as the Turyn construction of the Leech lattice.
, Λ2 is to the hexagonal lattice
, and Λ3 is the face-centered cubic packing. showed that the Leech lattice is the unique laminated lattice in 24 dimensions.
is replaced with the ternary Golay code
, and the Mathieu group M24 is replaced with the Mathieu group M12. The E6 lattice, E8 lattice and Coxeter–Todd lattice also have constructions as complex lattices, over either the Eisenstein or Gaussian integers.
s. The icosian ring is abstractly isomorphic to the E8 lattice
, three copies of which can be used to construct the Leech lattice using the Turyn construction.
Co1; its order is 8 315 553 613 086 720 000. Many other sporadic simple groups, such as the remaining Conway groups and Mathieu groups, can be constructed as the stabilizers of various configurations of vectors in the Leech lattice.
Despite having such a high rotational symmetry group, the Leech lattice does not possess any lines of reflection symmetry. In other words, the Leech lattice is chiral.
The automorphism group was first described by John Conway
. The 398034000 vectors of norm 8 fall into 8292375 'crosses' of 48 vectors. Each cross contains 24 mutually orthogonal vectors and their inverses, and thus describe the vertices of a 24-dimensional octahedron
. Each of these crosses can be taken to be the coordinate system of the lattice, and has the same symmetry of the Golay code, namely 212 × |M24|. Hence the full automorphism group of the Leech lattice has order 8292375 × 4096 × 244823040, or 8 315 553 613 086 720 000.
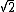; in other words, if we put a closed ball of this radius around each lattice point, then these just cover Euclidean space. The points at distance at least 
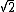from all lattice points are called the deep holes of the Leech lattice. There are 23 orbits of them under the automorphism group of the Leech lattice, and these orbits correspond to the 23 Niemeier lattices other than the Leech lattice: the set of vertices of deep hole is isometric to the affine Dynkin diagram of the corresponding Niemeier lattice.
The Leech lattice has a density of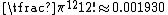
, correct to six decimal places. Cohn and Kumar showed that it gives the densest lattice packing of balls
in 24-dimensional space. Their results suggest, but do not prove, that this configuration also gives the densest among all packings of balls in 24-dimensional space. No arrangement of 24-dimensional spheres can be denser than the Leech lattice by a factor of more than 1.65×10−30, and it is highly probable that the Leech lattice is indeed optimal.
The 196560 minimal vectors are of three different varieties, known as shapes:
The ternary Golay code
, binary Golay code
and Leech lattice give very efficient 24-dimensional spherical code
s of 729, 4096 and 196560 points, respectively. Spherical codes are higher-dimensional analogues of Tammes problem
, which arose as an attempt to explain the distribution of pores on pollen grains. These are distributed as to maximise the minimal angle between them. In two dimensions, the problem is trivial, but in three dimensions and higher it is not. An example of a spherical code in three dimensions is the set of the 12 vertices of the regular icosahedron.
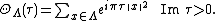
The theta function of a lattice is then a holomorphic function
on the upper half-plane. Furthermore, the theta function of an even unimodular lattice of rank n is actually a modular form
of weight n/2. The theta function of an integral lattice is often written as a power series in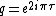
so that the coefficient of qn gives the number of lattice vectors of norm 2n. In the Leech lattice, there are 196560 vectors of norm 4, 16773120 vectors of norm 6, 398034000 vectors of norm 8 and so on. The theta series of the Leech lattice is thus:
where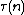
represents the Ramanujan tau function, and 
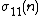is the divisor function
. It follows that the number of vectors of norm 2m is
describing bosonic string theory
, compactified on the 24-dimensional quotient
torus
R24/Λ24 and orbifold
ed by a two-element reflection group, provides an explicit construction of the Griess algebra
that has the monster group
as its automorphism group. This monster vertex algebra
was also used to prove the monstrous moonshine
conjectures.
The binary Golay code
, independently developed in 1949, is an application in coding theory
. More specifically, it is an error-correcting code capable of correcting up to three errors in each 24-bit word, and detecting a fourth. It was used to communicate with the Voyager probes, as it is much more compact than the previously-used Hadamard code
.
Quantizers, or analog-to-digital converter
s, can use lattices to minimise the average root-mean-square error. Most quantizers are based on the one-dimensional integer lattice
, but using multi-dimensional lattices reduces the RMS error. The Leech lattice is a good solution to this problem, as the Voronoi cells have a low second moment.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Leech lattice is an even unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
Λ24 in 24-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
E24 found by .
History
Many of the cross-sections of the Leech lattice, including the Coxeter–Todd lattice and Barnes–Wall lattice, in 12 and 16 dimensions, were found much earlier than the Leech lattice. discovered a related odd unimodular lattice in 24 dimensions, now called the odd Leech lattice, whose even sublattice has index 2 in the Leech lattice. The Leech lattice was discovered in 1965 by , by improving some earlier sphere packings he found in .calculated the order of the automorphism group of the Leech lattice, and discovered three new sporadic group
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
s as a by-product: the Conway groups, Co1, Co2, Co3.
, has a single rather cryptic sentence mentioning that he found more than 10 even unimodular lattices in 24 dimensions without giving further details.
In a seminar in 1970 Ernst Witt
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
claimed that one of the lattices he found in 1940 was the Leech lattice. See his collected works for more comments and for some notes Witt wrote about this in 1972.
Characterization
The Leech lattice Λ24 is the unique lattice in E24 with the following list of properties:- It is unimodularUnimodular latticeIn mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
; i.e., it can be generated by the columns of a certain 24×24 matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1. - It is even; i.e., the square of the length of any vector in Λ24 is an even integer.
- The length of any non-zero vector in Λ24 is at least 2.
Properties
The last condition is equivalent to the condition that unit balls centered at the points of Λ24 do not overlap. Each is tangent to 196,560 neighbors, and this is known to be the largest number of non-overlapping 24-dimensional unit balls that can simultaneously touch a single unit ball (compare with 6 in dimension 2, as the maximum number of pennies which can touch a central penny; see kissing number). This arrangement of 196560 unit balls centred about another unit ball is so efficient that there is no room to move any of the balls; this configuration, together with its mirror-image, is the only 24-dimensional arrangement where 196560 unit balls simultaneously touch another. This property is also true in 1, 2 and 8 dimensions, with 2, 6 and 240 unit balls, respectively, based on the integer latticeInteger lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
, hexagonal tiling and E8 lattice
E8 lattice
In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
, respectively.
It has no root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
and in fact is the first unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
with no roots (vectors of norm less than 4), and therefore has a centre density of 1. By multiplying this value by the volume of a unit ball in 24 dimensions,
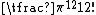, one can derive its absolute density.showed that the Leech lattice is isometric to the set of simple roots (or the Dynkin diagram) of the reflection group
Reflection group
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
of the 26-dimensional even Lorentzian unimodular lattice II25,1. By comparison, the Dynkin diagrams of II9,1 and II17,1 are finite.
Constructions
The Leech lattice can be constructed in a variety of ways. As with all lattices, it can be constructed via its generator matrixGenerator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
, a 24×24 matrix with determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
1.
Using the binary Golay code
The Leech lattice can be explicitly constructed as the set of vectors of the form 2−3/2(a1, a2, ..., a24) where the ai are integers such thatand for each fixed residue class modulo 4, the 24 bit word, whose 1's correspond to the coordinates i such that ai belongs to this residue class, is a word in the binary Golay code
Binary Golay code
In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
. The Golay code, together with the related Witt Design, features in a construction for the 196560 minimal vectors in the Leech lattice.
Using the Lorentzian lattice II25,1
The Leech lattice can also be constructed as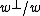 where w is the Weyl vector: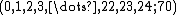in the 26-dimensional even Lorentzian unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
II25,1
II25,1
In mathematics, II25,1 is the even 26-dimensional Lorentzian unimodular lattice. It has several unusual properties, arising from Conway's discovery that it has a norm zero Weyl vector...
. The existence of such an integral vector of norm zero relies on the fact that 12 + 22 + ... + 242 is a perfect square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
(in fact 702); the number 24 is the only integer bigger than 1 with this property. This was conjectured by Édouard Lucas
Edouard Lucas
François Édouard Anatole Lucas was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him.-Biography:...
, but the proof came much later, based on elliptic functions.
The vector
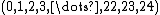
in this construction is really the Weyl vector of the even sublattice D24 of the odd unimodular lattice I25. More generally, if L is any positive definite unimodular lattice of dimension 25 with at least 4 vectors of norm 1, then the Weyl vector of its norm 2 roots has integral length, and there is a similar construction of the Leech lattice using L and this Weyl vector.
Based on other lattices
described another 23 constructions for the Leech lattice, each based on a Niemeier latticeNiemeier lattice
In mathematics, a Niemeier lattice is one of the 24positive definite even unimodular lattices of rank 24,which were classified by . gave a simplified proof of the classification. has a sentence mentioning that he found more than 10 such lattices, but gives no further details...
. It can also be constructed by using three copies of the E8 lattice
E8 lattice
In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
, in the same way that the binary Golay code can be constructed using three copies of the extended Hamming code
Hamming code
In telecommunication, Hamming codes are a family of linear error-correcting codes that generalize the Hamming-code invented by Richard Hamming in 1950. Hamming codes can detect up to two and correct up to one bit errors. By contrast, the simple parity code cannot correct errors, and can detect only...
, H8. This construction is known as the Turyn construction of the Leech lattice.
As a laminated lattice
Starting with a single point, Λ0, one can stack copies of the lattice Λn to form an (n + 1)-dimensional lattice, Λn+1, without reducing the minimal distance between points. Λ1 corresponds to the integer latticeInteger lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
, Λ2 is to the hexagonal lattice
Hexagonal lattice
The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
, and Λ3 is the face-centered cubic packing. showed that the Leech lattice is the unique laminated lattice in 24 dimensions.
As a complex lattice
The Leech lattice is also a 12-dimensional lattice over the Eisenstein integers. This is known as the complex Leech lattice, and is isomorphic to the 24-dimensional real Leech lattice. In the complex construction of the Leech lattice, the binary Golay codeBinary Golay code
In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
is replaced with the ternary Golay code
Ternary Golay code
There are two closely related error-correcting codes known as ternary Golay codes. The code generally known simply as the ternary Golay code is a perfect [11, 6, 5] ternary linear code; the extended ternary Golay code is a [12, 6, 6] linear code obtained by adding a zero-sum check digit to the...
, and the Mathieu group M24 is replaced with the Mathieu group M12. The E6 lattice, E8 lattice and Coxeter–Todd lattice also have constructions as complex lattices, over either the Eisenstein or Gaussian integers.
Using the icosian ring
The Leech lattice can also be constructed using the ring of icosianIcosian
In mathematics, the icosians are a specific set of Hamiltonian quaternions with the same symmetry as the 600-cell. The term can be used to refer to two related, but distinct, concepts:...
s. The icosian ring is abstractly isomorphic to the E8 lattice
E8 lattice
In mathematics, the E8 lattice is a special lattice in R8. It can be characterized as the unique positive-definite, even, unimodular lattice of rank 8...
, three copies of which can be used to construct the Leech lattice using the Turyn construction.
Symmetries
The Leech lattice is highly symmetrical. Its automorphism group is the double cover of the Conway groupConway group
In mathematics, the Conway groups Co1, Co2, and Co3 are three sporadic groups discovered by John Horton Conway.The largest of the Conway groups, Co1, of order...
Co1; its order is 8 315 553 613 086 720 000. Many other sporadic simple groups, such as the remaining Conway groups and Mathieu groups, can be constructed as the stabilizers of various configurations of vectors in the Leech lattice.
Despite having such a high rotational symmetry group, the Leech lattice does not possess any lines of reflection symmetry. In other words, the Leech lattice is chiral.
The automorphism group was first described by John Conway
John Conway
John Conway may refer to:* John Horton Conway, mathematician at Princeton University. Popularly known for Conway's Game of Life* John B. Conway, mathematician, functional analyst, George Washington University...
. The 398034000 vectors of norm 8 fall into 8292375 'crosses' of 48 vectors. Each cross contains 24 mutually orthogonal vectors and their inverses, and thus describe the vertices of a 24-dimensional octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. Each of these crosses can be taken to be the coordinate system of the lattice, and has the same symmetry of the Golay code, namely 212 × |M24|. Hence the full automorphism group of the Leech lattice has order 8292375 × 4096 × 244823040, or 8 315 553 613 086 720 000.
Geometry
showed that the covering radius of the Leech lattice is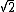; in other words, if we put a closed ball of this radius around each lattice point, then these just cover Euclidean space. The points at distance at least 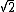from all lattice points are called the deep holes of the Leech lattice. There are 23 orbits of them under the automorphism group of the Leech lattice, and these orbits correspond to the 23 Niemeier lattices other than the Leech lattice: the set of vertices of deep hole is isometric to the affine Dynkin diagram of the corresponding Niemeier lattice.The Leech lattice has a density of
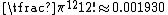, correct to six decimal places. Cohn and Kumar showed that it gives the densest lattice packing of ballsSphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
in 24-dimensional space. Their results suggest, but do not prove, that this configuration also gives the densest among all packings of balls in 24-dimensional space. No arrangement of 24-dimensional spheres can be denser than the Leech lattice by a factor of more than 1.65×10−30, and it is highly probable that the Leech lattice is indeed optimal.
The 196560 minimal vectors are of three different varieties, known as shapes:
- 1104 vectors of shape (42,022), for all permutations and sign choices;
- 97152 vectors of shape (28,016), where the '2's correspond to octads in the Golay code, and there an even number of minus signs;
- 98304 vectors of shape (3,123), where the signs come from the Golay code, and the '3' can appear in any position.
The ternary Golay code
Ternary Golay code
There are two closely related error-correcting codes known as ternary Golay codes. The code generally known simply as the ternary Golay code is a perfect [11, 6, 5] ternary linear code; the extended ternary Golay code is a [12, 6, 6] linear code obtained by adding a zero-sum check digit to the...
, binary Golay code
Binary Golay code
In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
and Leech lattice give very efficient 24-dimensional spherical code
Spherical code
In geometry and coding theory, a spherical code with parameters is a set of N points on the unit hypersphere in n dimensions for which the dot product of any two points is less than or equal to t...
s of 729, 4096 and 196560 points, respectively. Spherical codes are higher-dimensional analogues of Tammes problem
Tammes problem
In geometry, Tammes problem is a problem in packing a given number of circles on the surface of a sphere such that the minimum distance between circles is maximized. It is named after a Dutch botanist who posed the problem in 1930 while studying the distribution of pores on pollen grains...
, which arose as an attempt to explain the distribution of pores on pollen grains. These are distributed as to maximise the minimal angle between them. In two dimensions, the problem is trivial, but in three dimensions and higher it is not. An example of a spherical code in three dimensions is the set of the 12 vertices of the regular icosahedron.
Theta series
One can associate to any (positive-definite) lattice Λ a theta function given by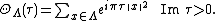The theta function of a lattice is then a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
on the upper half-plane. Furthermore, the theta function of an even unimodular lattice of rank n is actually a modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
of weight n/2. The theta function of an integral lattice is often written as a power series in
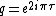so that the coefficient of qn gives the number of lattice vectors of norm 2n. In the Leech lattice, there are 196560 vectors of norm 4, 16773120 vectors of norm 6, 398034000 vectors of norm 8 and so on. The theta series of the Leech lattice is thus:
where
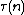represents the Ramanujan tau function, and 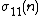is the divisor functionDivisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
. It follows that the number of vectors of norm 2m is
Applications
The vertex algebra of the conformal field theoryConformal field theory
A conformal field theory is a quantum field theory that is invariant under conformal transformations...
describing bosonic string theory
Bosonic string theory
Bosonic string theory is the original version of string theory, developed in the late 1960s.In the early 1970s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory became the real focus...
, compactified on the 24-dimensional quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
R24/Λ24 and orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
ed by a two-element reflection group, provides an explicit construction of the Griess algebra
Griess algebra
In mathematics, the Griess algebra is a commutative non-associative algebra on a real vector space of dimension 196884 that has the Monster group M as its automorphism group. It is named after mathematician R. L. Griess, who constructed it in 1980 and subsequently used it in 1982 to construct M...
that has the monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
as its automorphism group. This monster vertex algebra
Monster vertex algebra
The monster vertex algebra is a vertex algebra acted on by the monster group that was constructed by Igor Frenkel, James Lepowsky, and Arne Meurman. R...
was also used to prove the monstrous moonshine
Monstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
conjectures.
The binary Golay code
Binary Golay code
In mathematics and electronics engineering, a binary Golay code is a type of error-correcting code used in digital communications. The binary Golay code, along with the ternary Golay code, has a particularly deep and interesting connection to the theory of finite sporadic groups in mathematics....
, independently developed in 1949, is an application in coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
. More specifically, it is an error-correcting code capable of correcting up to three errors in each 24-bit word, and detecting a fourth. It was used to communicate with the Voyager probes, as it is much more compact than the previously-used Hadamard code
Hadamard code
The Hadamard code is an error-correcting code that is used for error detection and correction when transmitting messages over very noisy or unreliable channels....
.
Quantizers, or analog-to-digital converter
Analog-to-digital converter
An analog-to-digital converter is a device that converts a continuous quantity to a discrete time digital representation. An ADC may also provide an isolated measurement...
s, can use lattices to minimise the average root-mean-square error. Most quantizers are based on the one-dimensional integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
, but using multi-dimensional lattices reduces the RMS error. The Leech lattice is a good solution to this problem, as the Voronoi cells have a low second moment.