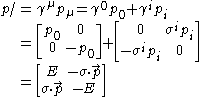Feynman slash notation
Encyclopedia
In the study of Dirac fields in quantum field theory
, Richard Feynman
invented the convenient Feynman slash notation (less commonly known as the Dirac
slash notation). If A is a covariant vector (i.e., a 1-form),
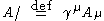
using the Einstein summation notation where γ are the gamma matrices.
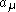 and
and 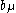 ,
,
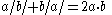 .
.
In particular,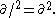
Further identities can be read off directly from the gamma matrix identities by replacing the metric tensor
with inner products. For example,
and solving for cross sections, one finds the slash notation used on four-momentum
:
using the Dirac basis for the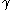 's,
's,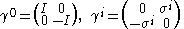
as well as the definition of four momentum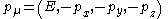
We see explicitly that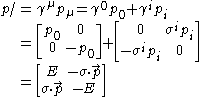
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
invented the convenient Feynman slash notation (less commonly known as the Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
slash notation). If A is a covariant vector (i.e., a 1-form),
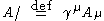
using the Einstein summation notation where γ are the gamma matrices.
Identities
Using the anticommutators of the gamma matrices, one can show that for any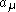 and
and 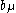 ,
,
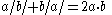 .
.In particular,
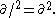
Further identities can be read off directly from the gamma matrix identities by replacing the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
with inner products. For example,
-
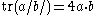
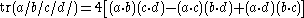
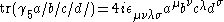
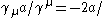 .
.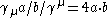
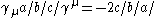
- where
 is the Levi-Civita symbolLevi-Civita symbolThe Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
is the Levi-Civita symbolLevi-Civita symbolThe Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
.
With four-momentum
Often, when using the Dirac equationDirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
and solving for cross sections, one finds the slash notation used on four-momentum
Four-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
:
using the Dirac basis for the
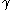 's,
's,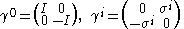
as well as the definition of four momentum
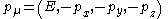
We see explicitly that