Statics
Encyclopedia
Statics is the branch of mechanics
concerned with the analysis of loads (force
, torque/moment
) on physical system
s in static equilibrium
, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity. When in static equilibrium, the system is either at rest, or its center of mass
moves at constant velocity.
By Newton's first law
, this situation implies that the net force and net torque
(also known as moment of force) on every body in the system is zero. From this constraint, such quantities as stress
or pressure
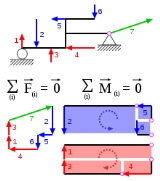
can be derived. The net forces equaling zero is known as the first condition for equilibrium, and the net torque equaling zero is known as the second condition for equilibrium. See statically determinate.
 A scalar is a quantity like mass or temperature which only has a magnitude. A vector is a quantity that has both a magnitude and a direction. There are many notations to identify a vector, the most common ones are:
A scalar is a quantity like mass or temperature which only has a magnitude. A vector is a quantity that has both a magnitude and a direction. There are many notations to identify a vector, the most common ones are:
Vectors can be added using the parallelogram law or the triangle law. Vectors contain components in orthogonal bases. Unit vectors i, j, and k are by convention along the x, y, and z directions.
Forces are classified as either contact or body forces. A contact force is produced by direct physical contact; an example is the force exerted on a body by a supporting surface. On the other hand, a body force is generated by virtue of the position of a body within a force field such as a gravitational, electric, or magnetic field. An example of a body force is your weight. (Meriam 2007 p. 24)
of the force. This rotational tendency is known as the moment M of the force. Moment is also referred to as torque.
M = Fd
where
F = The force applied
d = The perpendicular distance from the axis to the line of action of the force. Normally referred to as the moment arm.
The direction of the moment is given by the right hand rule, where counter clockwise (CCW) is out of the page, and clockwise (CW) is into the page. The moment direction may be accounted for by using a stated sign convention, such as a plus sign (+) for counterclockwise moments and a minus sign (-) for clockwise moments, or vice versa. Moments can be added together as vectors.
which states that the moment of a force about any point is equal to the sum of the moments of the components of the force about the same point.
, also called mass moment, rotational inertia, polar moment of inertia of mass, or the angular mass, (SI units kg·m²) is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation. The moment of inertia plays much the same role in rotational dynamics as mass does in linear dynamics, describing the relationship between angular momentum and angular velocity, torque and angular acceleration, and several other quantities. The symbol I and sometimes J are usually used to refer to the moment of inertia or polar moment of inertia.
While a simple scalar treatment of the moment of inertia suffices for many situations, a more advanced tensor treatment allows the analysis of such complicated systems as spinning tops and gyroscopic motion.
The concept was introduced by Leonhard Euler in his book Theoria motus corporum solidorum seu rigidorum in 1765.[1] In this book, he discussed the moment of inertia and many related concepts, such as the principal axis of inertia.
and structural engineering
. Strength of materials
is a related field of mechanics that relies heavily on the application of static equilibrium. A key concept is the center of gravity
of a body at rest: it represents an imaginary point at which all the mass
of a body resides. The position of the point relative to the foundations on which a body lies determines its stability
towards small movements. If the center of gravity exists outside the foundations, then the body is unstable because there is a torque acting: any small disturbance will cause the body to fall or topple. If the center of gravity exists within the foundations, the body is stable since no net torque acts on the body. If the center of gravity coincides with the foundations, then the body is said to be metastable.
, is the study of fluids at rest. This analyzes bodies of fluid in static equilibrium. The characteristic of any fluid at rest is that the force exerted on any particle of the fluid is the same at all points at the same depth (or altitude) within the fluid. If the net force is greater than zero the fluid will move in the direction of the resulting force. This concept was first formulated in a slightly extended form by the French
mathematician
and philosopher Blaise Pascal
in 1647 and would be later known as Pascal's Law
. This law has many important applications in hydraulics
. Archimedes
, Abū Rayhān al-Bīrūnī, Al-Khazini
and Galileo Galilei
were also major figures in the development of hydrostatics.
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
concerned with the analysis of loads (force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, torque/moment
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
) on physical system
Physical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
s in static equilibrium
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity. When in static equilibrium, the system is either at rest, or its center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
moves at constant velocity.
By Newton's first law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
, this situation implies that the net force and net torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
(also known as moment of force) on every body in the system is zero. From this constraint, such quantities as stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
or pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
can be derived. The net forces equaling zero is known as the first condition for equilibrium, and the net torque equaling zero is known as the second condition for equilibrium. See statically determinate.
Vectors

- A bold faced character V
- An underlined character V
- A character with an arrow over it
 .
.
Vectors can be added using the parallelogram law or the triangle law. Vectors contain components in orthogonal bases. Unit vectors i, j, and k are by convention along the x, y, and z directions.
Force
Force is the action of one body on another. A force tends to move a body in the direction of its action. The action of a force is characterized by its magnitude, by the direction of its action, and by its point of application. Thus force is a vector quantity, because its effect depends on the direction as well as on the magnitude of the action. (Meriam 2007 p. 23)Forces are classified as either contact or body forces. A contact force is produced by direct physical contact; an example is the force exerted on a body by a supporting surface. On the other hand, a body force is generated by virtue of the position of a body within a force field such as a gravitational, electric, or magnetic field. An example of a body force is your weight. (Meriam 2007 p. 24)
Moment of a force
In addition to the tendency to move a body in the direction of its application, a force can also tend to rotate a body about an axis. The axis may be any line which neither intersects nor is parallel to the line of actionLine of action
In physics, the line of action of a force F expresses the geometry of how F is applied. It is the line through the point at which F is applied and along the direction in which F is applied....
of the force. This rotational tendency is known as the moment M of the force. Moment is also referred to as torque.
Moment about a point
The magnitude of the moment of a force at a point O, is equal to the perpendicular distance from O to the line of action of F, multiplied by the magnitude of the force. Simply the magnitude of the moment is defined asM = Fd
where
F = The force applied
d = The perpendicular distance from the axis to the line of action of the force. Normally referred to as the moment arm.
The direction of the moment is given by the right hand rule, where counter clockwise (CCW) is out of the page, and clockwise (CW) is into the page. The moment direction may be accounted for by using a stated sign convention, such as a plus sign (+) for counterclockwise moments and a minus sign (-) for clockwise moments, or vice versa. Moments can be added together as vectors.
Varignon's theorem
One of the most useful principles of mechanics is Varignon's theoremVarignon's theorem
Varignon's theorem is a statement in Euclidean geometry by Pierre Varignon that was first published in 1731. It deals with the construction of a particular parallelogram from an arbitrary quadrangle....
which states that the moment of a force about any point is equal to the sum of the moments of the components of the force about the same point.
Equilibrium equations
The static equilibrium of a particle is an important concept in Statics. A particle is in equilibrium only if the resultant of all forces acting on the particle is equal to zero. In a rectangular coordinate system the equilibrium equations can be represented by three scalar equations, where the sum of forces in all three directions are equal to zero. An engineering application of this concept is determining the tensions of up to three cables under load, for example the forces exerted on each cable of a hoist lifting an object or of guy wires restraining a hot air balloon to the ground.Moment of inertia
In classical mechanics, moment of inertiaMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
, also called mass moment, rotational inertia, polar moment of inertia of mass, or the angular mass, (SI units kg·m²) is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation. The moment of inertia plays much the same role in rotational dynamics as mass does in linear dynamics, describing the relationship between angular momentum and angular velocity, torque and angular acceleration, and several other quantities. The symbol I and sometimes J are usually used to refer to the moment of inertia or polar moment of inertia.
While a simple scalar treatment of the moment of inertia suffices for many situations, a more advanced tensor treatment allows the analysis of such complicated systems as spinning tops and gyroscopic motion.
The concept was introduced by Leonhard Euler in his book Theoria motus corporum solidorum seu rigidorum in 1765.[1] In this book, he discussed the moment of inertia and many related concepts, such as the principal axis of inertia.
Solids
Statics is used in the analysis of structures, for instance in architecturalArchitectural engineering
Architectural engineering, also known as building engineering, is the application of engineering principles and technology to building design and construction...
and structural engineering
Structural engineering
Structural engineering is a field of engineering dealing with the analysis and design of structures that support or resist loads. Structural engineering is usually considered a specialty within civil engineering, but it can also be studied in its own right....
. Strength of materials
Strength of materials
In materials science, the strength of a material is its ability to withstand an applied stress without failure. The applied stress may be tensile, compressive, or shear. Strength of materials is a subject which deals with loads, deformations and the forces acting on a material. A load applied to a...
is a related field of mechanics that relies heavily on the application of static equilibrium. A key concept is the center of gravity
Center of gravity
In physics, a center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. In a uniform gravitational field, the center of mass serves as the center of gravity...
of a body at rest: it represents an imaginary point at which all the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of a body resides. The position of the point relative to the foundations on which a body lies determines its stability
Stability theory
In mathematics, stability theory addresses the stability of solutions of differential equations and of trajectories of dynamical systems under small perturbations of initial conditions...
towards small movements. If the center of gravity exists outside the foundations, then the body is unstable because there is a torque acting: any small disturbance will cause the body to fall or topple. If the center of gravity exists within the foundations, the body is stable since no net torque acts on the body. If the center of gravity coincides with the foundations, then the body is said to be metastable.
Fluids
Hydrostatics, also known as fluid staticsFluid statics
Fluid statics is the science of fluids at rest, and is a sub-field within fluid mechanics. The term usually refers to the mathematical treatment of the subject. It embraces the study of the conditions under which fluids are at rest in stable equilibrium...
, is the study of fluids at rest. This analyzes bodies of fluid in static equilibrium. The characteristic of any fluid at rest is that the force exerted on any particle of the fluid is the same at all points at the same depth (or altitude) within the fluid. If the net force is greater than zero the fluid will move in the direction of the resulting force. This concept was first formulated in a slightly extended form by the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
and philosopher Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
in 1647 and would be later known as Pascal's Law
Pascal's law
In the physical sciences, Pascal's law or the Principle of transmission of fluid-pressure states that "pressure exerted anywhere in a confined incompressible fluid is transmitted equally in all directions throughout the fluid such that the pressure ratio remains the same." The law was established...
. This law has many important applications in hydraulics
Hydraulics
Hydraulics is a topic in applied science and engineering dealing with the mechanical properties of liquids. Fluid mechanics provides the theoretical foundation for hydraulics, which focuses on the engineering uses of fluid properties. In fluid power, hydraulics is used for the generation, control,...
. Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
, Abū Rayhān al-Bīrūnī, Al-Khazini
Al-Khazini
Abu al-Fath Abd al-Rahman Mansour al-Khāzini or simply Abu al-Fath Khāzini was a Muslim astronomer of Greek ethnicity from Merv, then in the Khorasan province of Persia .-References:...
and Galileo Galilei
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
were also major figures in the development of hydrostatics.
See also
- DynamicsAnalytical dynamicsIn classical mechanics, analytical dynamics, or more briefly dynamics, is concerned about the relationship between motion of bodies and its causes, namely the forces acting on the bodies and the properties of the bodies...
- Mechanical equilibriumMechanical equilibriumA standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
- Solid mechanicsSolid mechanicsSolid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
- Cremona diagramCremona diagramThe Cremona diagram is a graphical method used in statics of trusses to determine the forces in members . The method was created by the Italian mathematician Luigi Cremona....
External links
- Online test of statics conceptual knowledge (meant for teachers)
- Free engineering Statics courseware with about 300 interactive exercises with hints and feedback : Carnegie Mellon Open Learning Initiative
- Statics for Robotics

