Gas - AbsoluteAstronomy.com

Gas is one of the three classical states of matter (the others being liquid

Liquid

Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...

and solid

Solid

Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...

). Near absolute zero

Absolute zero

Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....

, a substance exists as a solid

Solid

. As heat is added to this substance it melts into a liquid

Liquid

at its melting point

Melting point

The melting point of a solid is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends on pressure and is usually specified at standard atmospheric pressure...

(see phase change), boils into a gas at its boiling point

Boiling point

The boiling point of an element or a substance is the temperature at which the vapor pressure of the liquid equals the environmental pressure surrounding the liquid....

, and if heated high enough would enter a plasma

Plasma (physics)

In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...

state in which the electrons are so energized that they leave their parent atoms from within the gas. A pure gas may be made up of individual atoms (e.g. a noble gas

Noble gas

The noble gases are a group of chemical elements with very similar properties: under standard conditions, they are all odorless, colorless, monatomic gases, with very low chemical reactivity...

or atomic gas like neon

Neon

Neon is the chemical element that has the symbol Ne and an atomic number of 10. Although a very common element in the universe, it is rare on Earth. A colorless, inert noble gas under standard conditions, neon gives a distinct reddish-orange glow when used in either low-voltage neon glow lamps or...

), elemental

Chemical element

A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...

molecules made from one type of atom (e.g. oxygen

Oxygen

Oxygen is the element with atomic number 8 and represented by the symbol O. Its name derives from the Greek roots ὀξύς and -γενής , because at the time of naming, it was mistakenly thought that all acids required oxygen in their composition...

), or compound

Chemical compound

A chemical compound is a pure chemical substance consisting of two or more different chemical elements that can be separated into simpler substances by chemical reactions. Chemical compounds have a unique and defined chemical structure; they consist of a fixed ratio of atoms that are held together...

molecules made from a variety of atoms (e.g. carbon dioxide

Carbon dioxide

Carbon dioxide is a naturally occurring chemical compound composed of two oxygen atoms covalently bonded to a single carbon atom...

). A gas mixture

Mixture

In chemistry, a mixture is a material system made up by two or more different substances which are mixed together but are not combined chemically...

would contain a variety of pure gases much like the air

Earth's atmosphere

The atmosphere of Earth is a layer of gases surrounding the planet Earth that is retained by Earth's gravity. The atmosphere protects life on Earth by absorbing ultraviolet solar radiation, warming the surface through heat retention , and reducing temperature extremes between day and night...

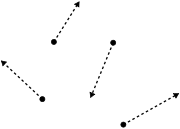
. What distinguishes a gas from liquids and solids is the vast separation of the individual gas particles. This separation usually makes a colorless gas invisible to the human observer. The interaction of gas particles in the presence of electric and gravitational fields are considered negligible as indicated by the constant velocity vectors in the image.

The gaseous state of matter is found between the liquid and plasma states, the latter of which provides the upper temperature boundary for gases. Bounding the lower end of the temperature

Temperature

Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...

scale lie degenerative quantum gases which are gaining increased attention these days. High-density atomic gases super cooled to incredibly low temperatures are classified by their statistical behavior as either a Bose gas

Bose gas

An ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...

or a Fermi gas

Fermi gas

A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...

. For a comprehensive listing of these exotic states of matter see list of states of matter.

Etymology

The word gas is a neologism first used by the early 17th century Flemish

Flemish people

The Flemings or Flemish are the Dutch-speaking inhabitants of Belgium, where they are mostly found in the northern region of Flanders. They are one of two principal cultural-linguistic groups in Belgium, the other being the French-speaking Walloons...

chemist

Chemist

A chemist is a scientist trained in the study of chemistry. Chemists study the composition of matter and its properties such as density and acidity. Chemists carefully describe the properties they study in terms of quantities, with detail on the level of molecules and their component atoms...

J.B. Van Helmont

Jan Baptist van Helmont

Jan Baptist van Helmont was an early modern period Flemish chemist, physiologist, and physician. He worked during the years just after Paracelsus and iatrochemistry, and is sometimes considered to be "the founder of pneumatic chemistry"...

. Van Helmont's word appears to have been simply a phonetic transcription of the Greek

Ancient Greek

Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...

word Chaos – the g in Dutch being pronounced like the English ch – in which case Van Helmont was simply following the established alchemical

Alchemy

Alchemy is an influential philosophical tradition whose early practitioners’ claims to profound powers were known from antiquity. The defining objectives of alchemy are varied; these include the creation of the fabled philosopher's stone possessing powers including the capability of turning base...

usage first attested in the works of Paracelsus

Paracelsus

Paracelsus was a German-Swiss Renaissance physician, botanist, alchemist, astrologer, and general occultist....

. According to Paracelsus's terminology, chaos meant something like "ultra-rarified water".

Physical characteristics

As most gases are difficult to observe directly with our senses, they are described through the use of four physical properties or macroscopic characteristics: pressure

Pressure

Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...

, volume, number of particles (chemists group them by moles

Mole (unit)

The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...

) and temperature

Temperature

. These four characteristics were repeatedly observed by scientists such as Robert Boyle

Robert Boyle

Robert Boyle FRS was a 17th century natural philosopher, chemist, physicist, and inventor, also noted for his writings in theology. He has been variously described as English, Irish, or Anglo-Irish, his father having come to Ireland from England during the time of the English plantations of...

, Jacques Charles

Jacques Charles

Jacques Alexandre César Charles was a French inventor, scientist, mathematician, and balloonist.Charles and the Robert brothers launched the world's first hydrogen-filled balloon in August 1783, then in December 1783, Charles and his co-pilot Nicolas-Louis Robert ascended to a height of about...

, John Dalton

John Dalton

John Dalton FRS was an English chemist, meteorologist and physicist. He is best known for his pioneering work in the development of modern atomic theory, and his research into colour blindness .-Early life:John Dalton was born into a Quaker family at Eaglesfield, near Cockermouth, Cumberland,...

, Joseph Gay-Lussac and Amedeo Avogadro

Amedeo Avogadro

Lorenzo Romano Amedeo Carlo Avogadro di Quaregna e di Cerreto, Count of Quaregna and Cerreto was an Italian savant. He is most noted for his contributions to molecular theory, including what is known as Avogadro's law...

for a variety of gases in various settings. Their detailed studies ultimately led to a mathematical relationship among these properties expressed by the ideal gas law

Ideal gas law

The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...

(see simplified models section below).

Gas particles are widely separated from one another, and as such are not as strongly intermolecularly bonded to the same degree as liquids or solids. These intermolecular forces result from electrostatic interactions between each gas particle. Like charged areas of different gas particles repel, while oppositely charged regions of different gas particles attract one another; gases that contain permanently charged ions are known as plasma

Plasma (physics)

s. Gaseous compounds with polar covalent

Chemical polarity

In chemistry, polarity refers to a separation of electric charge leading to a molecule or its chemical groups having an electric dipole or multipole moment. Polar molecules interact through dipole–dipole intermolecular forces and hydrogen bonds. Molecular polarity is dependent on the difference in...

bonds contain permanent charge imbalances and so experience relatively strong intermolecular forces, although the molecule while the compound's net charge remains neutral. Transient, randomly-induced charges exist across non-polar covalent bond

Covalent bond

A covalent bond is a form of chemical bonding that is characterized by the sharing of pairs of electrons between atoms. The stable balance of attractive and repulsive forces between atoms when they share electrons is known as covalent bonding....

s of molecules and electrostatic interactions caused by them are referred to as Van der Waals force

Van der Waals force

In physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...

s. The interaction of these intermolecular forces varies within a substance which determines many of the physical properties unique to each gas. A quick comparison of boiling points for compounds formed by ionic and covalent bonds leads us to this conclusion. The drifting smoke particles in the image provides some insight into low pressure gas behavior.

Compared to the other states of matter, gases have an incredibly low density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...

and viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...

. Pressure

Pressure

and temperature

Temperature

influence the particles within a certain volume. This variation in particle separation and speed is referred to as compressibility. This particle separation and size influences optical properties of gases as can be found in the following list of refractive indices. Finally, gas particles spread apart or diffuse

Diffusion

Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...

in order to homogeneously distribute themselves throughout any container.

Macroscopic

When observing a gas, it is typical to specify a frame of reference or length scale

Length scale

In physics, length scale is a particular length or distance determined with the precision of one order of magnitude. The concept of length scale is particularly important because physical phenomena of different length scales cannot affect each other and are said to decouple...

. A larger length scale corresponds to a macroscopic

Macroscopic

The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...

or global point of view of the gas. This region (referred to as a volume) must be sufficient in size to contain a large sampling of gas particles. The resulting statistical analysis of this sample size produces the "average" behavior (i.e. velocity, temperature or pressure) of all the gas particles within the region. By way of contrast, a smaller length scale corresponds to a microscopic

Microscopic

The microscopic scale is the scale of size or length used to describe objects smaller than those that can easily be seen by the naked eye and which require a lens or microscope to see them clearly.-History:...

or particle point of view.

From this global vantage point, the gas characteristics measured are either in terms of the gas particles themselves (velocity, pressure, or temperature) or their surroundings (volume). By way of example, Robert Boyle studied pneumatic chemistry

Pneumatic chemistry

Pneumatic chemistry is a term most-closely identified with an area of scientific research of the seventeenth, eighteenth, and early nineteenth centuries. Important goals of this work were an understanding of the physical properties of gases and how they relate to chemical reactions and,...

for a small portion of his career. One of his experiments related the macroscopic

Macroscopic

properties of pressure and volume of a gas. His experiment used a J-tube manometer which looks like a test tube

Test tube

A test tube, also known as a culture tube or sample tube, is a common piece of laboratory glassware consisting of a finger-like length of glass or clear plastic tubing, open at the top, usually with a rounded U-shaped bottom....

in the shape of the letter J. Boyle trapped an inert

Inert

-Chemistry:In chemistry, the term inert is used to describe a substance that is not chemically reactive.The noble gases were previously known as inert gases because of their perceived lack of participation in any chemical reactions...

gas in the closed end of the test tube with a column of mercury

Mercury (element)

Mercury is a chemical element with the symbol Hg and atomic number 80. It is also known as quicksilver or hydrargyrum...

, thereby locking the number of particles and temperature. He observed that when the pressure was increased on the gas, by adding more mercury to the column, the trapped gas volume decreased. Mathematicians describe this situation as an inverse

Inverse (mathematics)

In many contexts in mathematics the term inverse indicates the opposite of something. This word and its derivatives are used widely in mathematics, as illustrated below....

relationship. Furthermore, when Boyle multiplied the pressure and volume of each observation, the product (math) was always the same, a constant. This relationship held true for every gas that Boyle observed leading to the law, (PV=k), named to honor his work in this field of study.

There are many math tools to choose from when analyzing gas properties. As gases are subjected to extreme conditions, the math tools become a bit more complex, from the Euler equations

Euler equations

In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...

(inviscid flow) to the Navier-Stokes equations

Navier-Stokes equations

In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...

that fully account for viscous effects. These equations are tailored to meet the unique conditions of the gas system in question. Boyle's lab equipment allowed the use of algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

to obtain his analytical results. His results were possible because he was studying gases in relatively low pressure situations where they behaved in an "ideal" manner. These ideal relationships enable safety calculations for a variety of flight conditions on the materials in use. The high technology equipment in use today was designed to help us safely explore the more exotic operating environments where the gases no longer behave in an "ideal" manner. This advanced math, to include statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

and multivariable calculus

Multivariable calculus

Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....

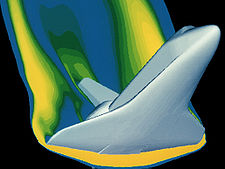
, makes possible the solution to such complex dynamic situations as space vehicle reentry. One such example might be the analysis of the image depicting space shuttle reentry to ensure the material properties under this loading condition are not exceeded. It is safe to say that in this flight regime, the gas is no longer behaving ideally.

Pressure

The symbol used to represent pressure in equations is "p" or "P" with SI units of pascals

Pascal (unit)

The pascal is the SI derived unit of pressure, internal pressure, stress, Young's modulus and tensile strength, named after the French mathematician, physicist, inventor, writer, and philosopher Blaise Pascal. It is a measure of force per unit area, defined as one newton per square metre...

.

When describing a container of gas, the term pressure

Pressure

(or absolute pressure) refers to the average force the gas exerts on the surface area of the container. Within this volume, it is sometimes easier to visualize the gas particles moving in straight lines until they collide with the container (see diagram at top of the article). The force imparted by a gas particle into the container during this collision is the change in momentum

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

of the particle. As a reminder from classical mechanics

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

, momentum, by definition, is the product of mass and velocity. Notice that during a collision only the normal component of velocity changes. A particle traveling parallel to the wall never changes its momentum. So the average force on a surface must be the average change in linear momentum from all of these gas particle collisions. To be more precise, pressure is the sum of all the normal components of force exerted by the particles impacting the walls of the container divided by the surface area of the wall. The image "Pressurized gases" depicts gas pressure and temperature spikes used in the entertainment industry.

Temperature

The symbol used to represent temperature in equations is T with SI units of kelvin

Kelvin

The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...

s.

The speed of a gas particle is proportional to its absolute temperature. The volume of the balloon in the video shrinks when the trapped gas particles slow down with the addition of extremely cold nitrogen. The temperature of any physical system

Physical system

In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...

is related to the motions of the particles (molecules and atoms) which make up the [gas] system. In statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

, temperature is the measure of the average kinetic energy stored in a particle. The methods of storing this energy are dictated by the degrees of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

of the particle itself (energy modes). Kinetic energy added (endothermic

Endothermic

In thermodynamics, the word endothermic describes a process or reaction in which the system absorbs energy from the surroundings in the form of heat. Its etymology stems from the prefix endo- and the Greek word thermasi,...

process) to gas particles by way of collisions produces linear, rotational, and vibrational motion as well. By contrast, a molecule in a solid can only increase its vibration modes with the addition of heat as the lattice crystal structure prevents both linear and rotational motions. These heated gas molecules have a greater speed range which constantly varies due to constant collisions with other particles. The speed range can be described by the Maxwell-Boltzmann distribution. Use of this distribution implies ideal gas

Ideal gas

An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...

es near thermodynamic equilibrium

Thermodynamic equilibrium

In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...

for the system of particles being considered.

Specific volume

The symbol used to represent specific volume in equations is "v" with SI units of cubic meters per kilogram.
The symbol used to represent volume in equations is "V" with SI units of cubic meters.

When performing a thermodynamic analysis, it is typical to speak of intensive and extensive properties

Intensive and extensive properties

In the physical sciences, an intensive property , is a physical property of a system that does not depend on the system size or the amount of material in the system: it is scale invariant.By contrast, an extensive property In the physical sciences, an intensive property (also called a bulk...

. Properties which depend on the amount of gas (either by mass or volume) are called extensive properties, while properties that do not depend on the amount of gas are called intensive properties. Specific volume is an example of an intensive property because it is the ratio of volume occupied by a unit of mass of a gas that is identical throughout a system at equilibrium. 1000 atoms of protactinium

Protactinium

Protactinium is a chemical element with the symbol Pa and atomic number 91. It is a dense, silvery-gray metal which readily reacts with oxygen, water vapor and inorganic acids. It forms various chemical compounds where protactinium is usually present in the oxidation state +5, but can also assume...

as a gas occupy the same space as any other 1000 atoms for any given temperature and pressure. This concept is easier to visualize for solids such as iron

Iron

Iron is a chemical element with the symbol Fe and atomic number 26. It is a metal in the first transition series. It is the most common element forming the planet Earth as a whole, forming much of Earth's outer and inner core. It is the fourth most common element in the Earth's crust...

which are incompressible compared to gases. When the seat ejection is initiated in the rocket sled image the specific volume increases with the expanding gases, while mass is conserved. Since a gas fills any container in which it is placed, volume is an extensive property.

Density

The symbol used to represent density in equations is ρ with SI units of kilograms per cubic meter. This term is the reciprocal

Multiplicative inverse

In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...

of specific volume.

Since gas molecules can move freely within a container, their mass is normally characterized by density. Density is the mass per volume of a substance or simply, the inverse of specific volume. For gases, the density can vary over a wide range because the particles are free to move closer together when constrained by pressure or volume or both. This variation of density is referred to as compressibility. Like pressure and temperature, density is a state variable

State variable

A state variable is one of the set of variables that describe the "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour...

of a gas and the change in density during any process is governed by the laws of thermodynamics. For a static gas

Fluid statics

Fluid statics is the science of fluids at rest, and is a sub-field within fluid mechanics. The term usually refers to the mathematical treatment of the subject. It embraces the study of the conditions under which fluids are at rest in stable equilibrium...

, the density is the same throughout the entire container. Density is therefore a scalar quantity

Scalar (physics)

In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...

; it is a simple physical quantity that has a magnitude but no direction associated with it. It can be shown by kinetic theory that the density is inversely proportional to the size of the container in which a fixed mass of gas is confined. In this case of a fixed mass, the density decreases as the volume increases.

Microscopic

If one could observe a gas under a powerful microscope, one would see a collection of particles (molecules, atoms, ions, electrons, etc.) without any definite shape or volume that are in more or less random motion. These neutral gas particles only change direction when they collide with another particle or the sides of the container. By stipulating that these collisions are perfectly elastic, this substance is transformed from a real to an ideal gas. This particle or microscopic view of a gas is described by the Kinetic-molecular theory. All of the assumptions behind this theory can be found in the postulates section of Kinetic Theory

Kinetic theory

The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...

Kinetic theory

Kinetic theory provides insight into the macroscopic properties of gases by considering their molecular composition and motion. Starting with the definitions of momentum

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

and kinetic energy

Kinetic energy

The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...

, one can use the conservation of momentum

Conservation law

In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....

and geometric relationships of a cube to relate macro system properties of temperature and pressure to the microscopic property of kinetic energy per molecule. The theory provides averaged values for these two properties.

The theory also explains how the gas system responds to change. For example, as a gas is heated from absolute zero, when it is (in theory) perfectly still, its internal energy

Internal energy

In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...

(temperature) is increased. As a gas is heated, the particles speed up and its temperature rise. This results in greater numbers of collisions with the container sides each second due to the higher particle speeds associated with elevated temperatures. As the number of collisions (per unit time) increase on the surface area of the container, the pressure increases in a proportional manner.

Brownian motion

Brownian motion is the mathematical model used to describe the random movement of particles suspended in a fluid. The gas particle animation, using pink and green particles, illustrates how this behavior results in the spreading out of gases (entropy

Entropy

Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

). These events are also described by particle theory

Particle

A particle is, generally, a small localized object to which can be ascribed physical properties. It may also refer to:In chemistry:* Colloidal particle, part of a one-phase system of two or more components where the particles aren't individually visible.In physics:* Subatomic particle, which may be...

.

Since it is at the limit of (or beyond) current technology to observe individual gas particles (atoms or molecules), only theoretical calculations give suggestions as to how they move, but their motion is different from Brownian Motion. The reason is that Brownian Motion involves a smooth drag due to the frictional force of many gas molecules, punctuated by violent collisions of an individual (or several) gas molecule(s) with the particle. The particle (generally consisting of millions or billions of atoms) thus moves in a jagged course, yet not so jagged as would be expected if an individual gas molecule was examined.

Intermolecular forces

As discussed earlier, momentary attractions (or repulsions) between particles have an effect on gas dynamics

Gas dynamics

Gas dynamics is a branch of fluid dynamics concerned with studying the motion of gases and its consequent effects. Gas dynamics combines the principles of fluid mechanics and thermodynamics...

. In physical chemistry

Physical chemistry

Physical chemistry is the study of macroscopic, atomic, subatomic, and particulate phenomena in chemical systems in terms of physical laws and concepts...

, the name given to these intermolecular forces is van der Waals force. These forces play a key role in determining physical properties of a gas such as viscosity

Viscosity

Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...

and flow rate (see physical characteristics section). Ignoring these forces in certain conditions (see Kinetic-molecular theory) allows a real gas

Real gas

Real gases – as opposed to a perfect or ideal gas – exhibit properties that cannot be explained entirely using the ideal gas law. To understand the behaviour of real gases, the following must be taken into account:* compressibility effects;...

to be treated like an ideal gas

Ideal gas

. This assumption allows the use of ideal gas laws which greatly simplifies the path to a solution.

Proper use of these gas relationships requires us to take one more look at the Kinetic-molecular theory (KMT). When these gas particles possess a magnetic charge or Intermolecular force

Intermolecular force

Intermolecular forces are forces of attraction or repulsion which act between neighboring particles: atoms, molecules or ions. They are weak compared to the intramolecular forces, the forces which keep a molecule together...

they gradually influence one another as the spacing between them is reduced (the hydrogen bond model illustrates one example). In the absence of any charge, at some point when the spacing between gas particles is greatly reduced they can no longer avoid collisions between themselves at normal gas temperatures found in a lab. Another case for increased collisions among gas particles would include a fixed volume of gas, which upon heating would contain very fast particles. What this means to us is that these ideal equations provide reasonable results except for extremely high pressure [compressible] or high temperature [ionized] conditions. Notice that all of these excepted conditions allow energy transfer to take place within the gas system. The absence of these internal transfers is what is referred to as ideal conditions (perfect – or well behaved) in which the energy exchange occurs only at the boundaries of the system. Real gases experience some of these collisions and intermolecular forces. When these collisions are statistically negligible [incompressible], results from these ideal equations are still valid. At the other end of the spectrum, when the gas particles are compressed into close proximity they behave more like a liquid, and hence another connection to fluid dynamics

Fluid dynamics

In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

Simplified models

An equation of state (for gases) is a mathematical model used to roughly describe or predict the state properties of a gas. At present, there is no single equation of state that accurately predicts the properties of all gases under all conditions. Therefore, a number of much more accurate equations of state have been developed for gases in specific temperature and pressure ranges. The "gas models" that are most widely discussed are "perfect gas", "ideal gas" and "real gas". Each of these models has its own set of assumptions to facilitate the analysis of a given thermodynamic system. Each successive model expands the temperature range of coverage to which it applies. The image of first powered flight at Kitty Hawk, North Carolina

Kitty Hawk, North Carolina

Kitty Hawk is a town in Dare County, North Carolina, United States. The population was 3,000 at the 2000 census. It was established in the early 18th century as Chickahawk....

illustrates one example on the successful application of these relationships in 1903. More recent examples include the 2009 maiden flights of the first solar powered aircraft, the Solar Impulse

Solar Impulse

Solar Impulse is a Swiss long-range solar powered plane project being undertaken at the École Polytechnique Fédérale de Lausanne, by Bertrand Piccard and André Borschberg. The project eventually hopes to succeed in the first circling of the earth with a piloted fixed-wing aircraft using only solar...

, and the first commercial airliner to be constructed primarily from composite materials, the Dreamliner

Boeing 787

The Boeing 787 Dreamliner is a long-range, mid-size wide-body, twin-engine jet airliner developed by Boeing Commercial Airplanes. It seats 210 to 290 passengers, depending on the variant. Boeing states that it is the company's most fuel-efficient airliner and the world's first major airliner to use...

Ideal and perfect gas models

The equation of state

Equation of state

In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...

for an ideal or perfect gas is the ideal gas law

Ideal gas law

and reads

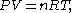
where P is the pressure, V is the volume, n is amount of gas (in mol units), R is the universal gas constant, 8.314 J/(mol K), and T is the temperature. Written this way, it is sometimes called the "chemist's version", since it emphasizes the number of molecules n. It can also be written as

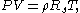
where

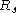is the specific gas constant for a particular gas, in units J/(kg K). This notation is the "gas dynamicist's" version, which is more practical in modeling of gas flows involving acceleration without chemical reactions.

The ideal gas law does not make an assumption about the specific heat of a gas. In the most general case, the specific heat is a function of both temperature and pressure. If the pressure-dependence is neglected (and possibly the temperature-dependence as well) in a particular application, sometimes the gas is said to be a perfect gas

Perfect gas

In physics, a perfect gas is a theoretical gas that differs from real gases in a way that makes certain calculations easier to handle. Its behavior is more simplified compared to an ideal gas...

, although the exact assumptions may vary depending on the author and/or field of science.

For an ideal gas, the ideal gas law applies without restrictions on the specific heat. An ideal gas is a simplified "real gas" with the assumption that the compressibility factor

Compressibility factor

The compressibility factor , also known as the compression factor, is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behavior. In general, deviation from ideal behavior becomes more significant the closer a gas is to a phase change, the lower the...

Z is set to 1 meaning that this pneumatic ratio remains constant. A compressibility factor of one also requires the four state variables to follow the ideal gas law

Ideal gas law

.

This approximation is more suitable for applications in engineering although simpler models can be used to produce a "ball-park" range as to where the real solution should lie. An example where the "ideal gas approximation" would be suitable would be inside a combustion chamber of a jet engine

Jet engine

A jet engine is a reaction engine that discharges a fast moving jet to generate thrust by jet propulsion and in accordance with Newton's laws of motion. This broad definition of jet engines includes turbojets, turbofans, rockets, ramjets, pulse jets...

. It may also be useful to keep the elementary reactions and chemical dissociations for calculating emissions

Exhaust gas

Exhaust gas or flue gas is emitted as a result of the combustion of fuels such as natural gas, gasoline/petrol, diesel fuel, fuel oil or coal. According to the type of engine, it is discharged into the atmosphere through an exhaust pipe, flue gas stack or propelling nozzle.It often disperses...

Real gas

Each one of the assumptions listed below adds to the complexity of the problem's solution. As the density of a gas increases with pressure rises, the intermolecular forces play a more substantial role in gas behavior which results in the ideal gas law no longer providing "reasonable" results. At the upper end of the engine temperature ranges (e.g. combustor sections – 1300 K), the complex fuel particles absorb internal energy by means of rotations and vibrations that cause their specific heats to vary from those of diatomic molecules and noble gases. At more than double that temperature, electronic excitation and dissociation of the gas particles begins to occur causing the pressure to adjust to a greater number of particles (transition from gas to plasma

Plasma (physics)

). Finally, all of the thermodynamic processes were presumed to describe uniform gases whose velocities varied according to a fixed distribution. Using a non-equilibrium situation implies the flow field must be characterized in some manner to enable a solution. One of the first attempts to expand the boundaries of the ideal gas law was to include coverage for different thermodynamic processes by adjusting the equation to read pVⁿ = constant and then varying the n through different values such as the specific heat ratio

Heat capacity ratio

The heat capacity ratio or adiabatic index or ratio of specific heats, is the ratio of the heat capacity at constant pressure to heat capacity at constant volume . It is sometimes also known as the isentropic expansion factor and is denoted by \gamma or \kappa . The latter symbol kappa is...

, γ.

Real gas effects include those adjustments made to account for a greater range of gas behavior:

Compressibility effects
Compressibility factor
The compressibility factor , also known as the compression factor, is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behavior. In general, deviation from ideal behavior becomes more significant the closer a gas is to a phase change, the lower the...

(Z allowed to vary from 1.0)
Variable heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...

(specific heats vary with temperature)
Van der Waals forces (related to compressibility, can substitute other equations of state)
Non-equilibrium thermodynamic effects
Non-equilibrium thermodynamics
Non-equilibrium thermodynamics is a branch of thermodynamics that deals with systems that are not in thermodynamic equilibrium. Most systems found in nature are not in thermodynamic equilibrium; for they are changing or can be triggered to change over time, and are continuously and discontinuously...
Issues with molecular dissociation
Dissociation (chemistry)
Dissociation in chemistry and biochemistry is a general process in which ionic compounds separate or split into smaller particles, ions, or radicals, usually in a reversible manner...

and elementary reaction
Elementary reaction
An elementary reaction is a chemical reaction in which one or more of the chemical species react directly to form products in a single reaction step and with a single transition state....

s with variable composition.

For most applications, such a detailed analysis is excessive. Examples where "Real Gas effects" would have a significant impact would be on the Space Shuttle

Space Shuttle

The Space Shuttle was a manned orbital rocket and spacecraft system operated by NASA on 135 missions from 1981 to 2011. The system combined rocket launch, orbital spacecraft, and re-entry spaceplane with modular add-ons...

re-entry

Atmospheric reentry

Atmospheric entry is the movement of human-made or natural objects as they enter the atmosphere of a celestial body from outer space—in the case of Earth from an altitude above the Kármán Line,...

where extremely high temperatures and pressures are present or the gases produced during geological events as in the image of the 1990 eruption of Mount Redoubt

Mount Redoubt

Mount Redoubt is the name of three mountains:* Mount Redoubt in Alaska, United States* Mount Redoubt in Washington, United States* Redoubt Mountain in Banff National Park, Canada...

Boyle's Law

Boyle's Law was perhaps the first expression of an equation of state. In 1662 Robert Boyle

Robert Boyle

performed a series of experiments employing a J-shaped glass tube, which was sealed on one end. Mercury was added to the tube, trapping a fixed quantity of air in the short, sealed end of the tube. Then the volume of gas was carefully measured as additional mercury was added to the tube. The pressure of the gas could be determined by the difference between the mercury level in the short end of the tube and that in the long, open end. Through these experiments, Boyle noted that the gas volume varied inversely with the pressure. The image of Boyle's Equipment shows some of the exotic tools used by Boyle during his study of gases.

Boyle's Law – describes a gas in which the number of particles and Temperature are constant.
PV = constant in this situation constant = nRT from the ideal gas law.

Law of volumes

In 1787, the French physicist and balloon pioneer, Jacques Charles

Jacques Charles

, found that oxygen, nitrogen, hydrogen, carbon dioxide, and air expand to the same extent over the same 80 kelvin interval.

In 1802, Joseph Louis Gay-Lussac

Joseph Louis Gay-Lussac

- External links :* from the American Chemical Society* from the Encyclopædia Britannica, 10th Edition * , Paris...

published results of similar, though more extensive experiments, indicating a linear relationship between volume and temperature. Gay-Lussac credited Charle's earlier work by naming the law in his honor. In the absence of this linkage, Dalton could have been in contention for this honor for his previously published work on partial pressures.

Law of Volumes – Both Charles and Gay-Lussac played a role in developing this relationship.
V/T = constant – notice that constant = nR/P from the ideal gas law.

Avogadro's Law

In 1811, Amedeo Avogadro verified that equal volumes of pure gases contain the same number of particles. His theory was not generally accepted until 1858 when another Italian chemist Stanislao Cannizzaro was able to explain non-ideal exceptions. For his work with gases a century prior, the number that bears his name Avogadro's constant represents the number of atoms found in 12 grams of elemental carbon-12 (6.022×10²³ mol⁻¹). This specific number of gas particles, at standard temperature and pressure (ideal gas law) occupies 22.40 liters, which is referred to as the molar volume

Molar volume

The molar volume, symbol Vm, is the volume occupied by one mole of a substance at a given temperature and pressure. It is equal to the molar mass divided by the mass density...

Avogadro's Law – describes a gas in a container in which the pressure and temperature are constant. The simplified form for the ideal gas law follows:
V/n = constant – notice that constant = RT/P from the ideal gas law.

Dalton's Law

In 1801, John Dalton

John Dalton

published the Law of Partial Pressures from his work with ideal gas law relationship: The pressure of a mixture of gases is equal to the sum of the pressures of all of the constituent gases alone. Mathematically, this can be represented for n species as:

Pressure_total = Pressure₁ + Pressure₂ + ... + Pressure_n

The image of Dalton's journal depicts symbology he used as shorthand to record the path he followed. Among his key journal observations upon mixing unreactive "elastic fluids" (gases) were the following.:

Unlike liquids, heavier gases did not drift to the bottom upon mixing.
Gas particle identity played no role in determining final pressure (they behaved as if their size was negligible).

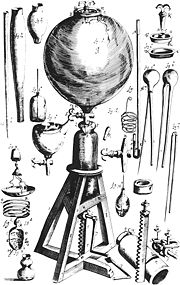
Compressibility

Thermodynamicists use this factor (Z) to alter the ideal gas equation to account for compressibility effects of real gases. This factor represents the ratio of actual to ideal specific volumes. It is sometimes referred to as a "fudge-factor" or correction to expand the useful range of the ideal gas law for design purposes. Usually this Z value is very close to unity. The compressibility factor image illustrates how Z varies over a range of very cold temperatures.

Reynolds number

In fluid mechanics, the Reynolds number is the ratio of inertial forces (v_sρ) to viscous forces (μ/L). It is one of the most important dimensionless numbers in fluid dynamics and is used, usually along with other dimensionless numbers, to provide a criterion for determining dynamic similitude. As such, the Reynolds number provides the link between modeling results (design) and the full-scale actual conditions. It can also be used to characterize the flow.

Viscosity

Viscosity, a physical property, is a measure of how well adjacent molecules stick to one another. A solid can withstand a shearing force due to the strength of these sticky intermolecular forces. A fluid will continuously deform when subjected to a similar load. While a gas has a lower value of viscosity than a liquid, it is still an observable property. If gases had no viscosity, then they would not stick to the surface of a wing and form a boundary layer. A study of the delta wing

Delta wing

The delta wing is a wing planform in the form of a triangle. It is named for its similarity in shape to the Greek uppercase letter delta .-Delta-shaped stabilizers:...

in the Schlieren

Schlieren photography

Schlieren photography is a visual process that is used to photograph the flow of fluids of varying density. Invented by the German physicist August Toepler in 1864 to study supersonic motion, it is widely used in aeronautical engineering to photograph the flow of air around objects...

image reveals that the gas particles stick to one another (see Boundary layer section).

Turbulence

In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic, stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time. The Satellite view of weather around Robinson Crusoe Islands illustrates just one example.

Boundary layer

Particles will, in effect, "stick" to the surface of an object moving through it. This layer of particles is called the boundary layer. At the surface of the object, it is essentially static due to the friction of the surface. The object, with its boundary layer is effectively the new shape of the object that the rest of the molecules "see" as the object approaches. This boundary layer can separate from the surface, essentially creating a new surface and completely changing the flow path. The classical example of this is a stalling airfoil. The delta wing image clearly shows the boundary layer thickening as the gas flows from right to left along the leading edge.

Maximum entropy principle

As the total number of degrees of freedom approaches infinity, the system will be found in the macrostate that corresponds to the highest multiplicity

Multiplicity (mathematics)

In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....

. In order to illustrate this principle, observe the skin temperature of a frozen metal bar. Using a thermal image of the skin temperature, note the temperature distribution on the surface. This initial observation of temperature represents a "microstate

Microstate

A microstate or ministate is a sovereign state having a very small population or very small land area, but usually both. Some examples include Liechtenstein, Malta, Monaco, Nauru, Singapore, and Vatican City....

." At some future time, a second observation of the skin temperature produces a second microstate. By continuing this observation process, it is possible to produce a series of microstates that illustrate the thermal history of the bar's surface. Characterization of this historical series of microstates is possible by choosing the macrostate that successfully classifies them all into a single grouping.

Thermodynamic equilibrium

When energy transfer ceases from a system, this condition is referred to as thermodynamic equilibrium. Usually this condition implies the system and surroundings are at the same temperature so that heat no longer transfers between them. It also implies that external forces are balanced (volume does not change), and all chemical reactions within the system are complete. The timeline varies for these events depending on the system in question. A container of ice allowed to melt at room temperature takes hours, while in semiconductors the heat transfer that occurs in the device transition from an on to off state could be on the order of a few nanoseconds.

Etymology

Physical characteristics

Macroscopic

Pressure

Temperature

Specific volume

Density

Microscopic

Kinetic theory

Brownian motion

Intermolecular forces

Simplified models

Ideal and perfect gas models

Real gas

Boyle's Law

Law of volumes

Avogadro's Law

Dalton's Law

Compressibility

Reynolds number

Viscosity

Turbulence

Boundary layer

Maximum entropy principle

Thermodynamic equilibrium

See also

Further reading