
Axiom of determinacy
Encyclopedia
The axiom of determinacy (abbreviated as AD) is a possible axiom
for set theory
introduced by Jan Mycielski
and Hugo Steinhaus
in 1962. It refers to certain two-person games of length ω
with perfect information
. AD states that every such game in which both players choose integer
s is determined; that is, one of the two players has a winning strategy.
The axiom of determinacy is inconsistent with the axiom of choice (AC); the axiom of determinacy implies that all subsets of the real number
s are Lebesgue measurable, have the property of Baire, and the perfect set property
. The last implies a weak form of the continuum hypothesis
(namely, that every uncountable
set of reals has the same cardinality as the full set of reals).
Furthermore, AD implies the consistency of Zermelo–Fraenkel set theory
(ZF). Hence, as a consequence of the incompleteness theorems
, it is not possible to prove the relative consistency of ZF + AD with respect to ZF.
that games whose winning set is a Borel set
are determined. It follows from the existence of sufficient large cardinals that all games with winning set a projective set are determined (see Projective determinacy), and that AD holds in L(R)
.
. The same is true of the set S2 of all second player strategies. We note that the cardinality of the set SG of all sequences possible in G is also the continuum. Let A be the subset of SG of all sequences which make the first player win. With the axiom of choice we can well order the continuum; furthermore, we can do so in such a way that any proper initial portion does not have the cardinality of the continuum. We create a counterexample by transfinite induction
on the set of strategies under this well ordering:
We start with the set A undefined. Let T be the "time" whose axis has length continuum. We need to consider all strategies {s1(T)} of the first player and all strategies {s2(T)} of the second player to make sure that for every strategy there is a strategy of the other player that wins against it. For every strategy of the player considered we will generate a sequence which gives the other player a win. Let t be the time whose axis has length ℵ0 and which is used during each game sequence.
Once this has been done we have a game G. If you give me a strategy s1 then we considered that strategy at some time T = T(s1). At time T, we decided an outcome of s1 that would be a loss of s1. Hence this strategy fails. But this is true for an arbitrary strategy; hence the axiom of determinacy and the axiom of choice are incompatible.
were proposed in the late 20th century. One reason that has been given for believing in the axiom of determinacy is that it can be written as follows (in a version of infinite logic):
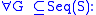
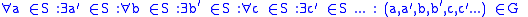 OR
OR
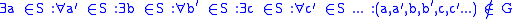
Note: Seq(S) is the set of all -sequences of S. The sentences here are infinitely long with a countably infinite list of quantifiers where the ellipses appear.
-sequences of S. The sentences here are infinitely long with a countably infinite list of quantifiers where the ellipses appear.
In an infinitary logic, this principle is therefore a natural generalization of the usual (de Morgan) rule for quantifiers that
are true for finite formulas, such as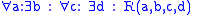 OR
OR 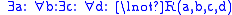 .
.
, the consistency of Zermelo–Fraenkel set theory without choice (ZF) together with the axiom of determinacy is equivalent to the consistency of Zermelo–Fraenkel set theory with choice (ZFC) together with the existence of infinitely many Woodin cardinal
s. Since Woodin cardinals are strongly inaccessible
, if AD is consistent, then so are an infinity of inaccessible cardinals.
Moreover, if to the hypothesis of an infinite set of Woodin cardinals is added the existence of a measurable cardinal
larger than all of them, a very strong theory of Lebesgue measurable sets of reals emerges, as it is then provable that the axiom of determinacy is true in L(R)
, and therefore that every set of real numbers in L(R) is determined.
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
for set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
introduced by Jan Mycielski
Jan Mycielski
Jan Mycielski is a Polish-American mathematician, a professor emeritus of mathematics at the University of Colorado at Boulder....
and Hugo Steinhaus
Hugo Steinhaus
Władysław Hugo Dionizy Steinhaus was a Polish mathematician and educator. Steinhaus obtained his PhD under David Hilbert at Göttingen University in 1911 and later became a professor at the University of Lwów, where he helped establish what later became known as the Lwów School of Mathematics...
in 1962. It refers to certain two-person games of length ω
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
with perfect information
Perfect information
In game theory, perfect information describes the situation when a player has available the same information to determine all of the possible games as would be available at the end of the game....
. AD states that every such game in which both players choose integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is determined; that is, one of the two players has a winning strategy.
The axiom of determinacy is inconsistent with the axiom of choice (AC); the axiom of determinacy implies that all subsets of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s are Lebesgue measurable, have the property of Baire, and the perfect set property
Perfect set property
In descriptive set theory, a subset of a Polish space has the perfect set property if it is either countable or has a nonempty perfect subset...
. The last implies a weak form of the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
(namely, that every uncountable
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
set of reals has the same cardinality as the full set of reals).
Furthermore, AD implies the consistency of Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
(ZF). Hence, as a consequence of the incompleteness theorems
Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
, it is not possible to prove the relative consistency of ZF + AD with respect to ZF.
Types of game that are determined
Not all games require the axiom of determinacy to prove them determined. Games whose winning sets are closed are determined. These correspond to many naturally defined infinite games. It was shown in 1975 by Donald A. MartinDonald A. Martin
Donald A. Martin is a set theorist and philosopher of mathematics at UCLA, where he is a member of the faculty of mathematics and philosophy....
that games whose winning set is a Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
are determined. It follows from the existence of sufficient large cardinals that all games with winning set a projective set are determined (see Projective determinacy), and that AD holds in L(R)
L(R)
In set theory, L is the smallest transitive inner model of ZF containing all the ordinals and all the reals. It can be constructed in a manner analogous to the construction of L , by adding in all the reals at the start, and then iterating the definable powerset operation through all the...
.
The axiom of choice and the axiom of determinacy are incompatible
The set S1 of all first player strategies in an ω-game G has the same cardinality as the continuumCardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
. The same is true of the set S2 of all second player strategies. We note that the cardinality of the set SG of all sequences possible in G is also the continuum. Let A be the subset of SG of all sequences which make the first player win. With the axiom of choice we can well order the continuum; furthermore, we can do so in such a way that any proper initial portion does not have the cardinality of the continuum. We create a counterexample by transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
on the set of strategies under this well ordering:
We start with the set A undefined. Let T be the "time" whose axis has length continuum. We need to consider all strategies {s1(T)} of the first player and all strategies {s2(T)} of the second player to make sure that for every strategy there is a strategy of the other player that wins against it. For every strategy of the player considered we will generate a sequence which gives the other player a win. Let t be the time whose axis has length ℵ0 and which is used during each game sequence.
- Consider the current strategy {s1(T)} of the first player.
- Go through the entire game, generating (together with the first player's strategy s1(T)) a sequence {a(1), b(2), a(3), b(4),...,a(t), b(t+1),...}.
- Decide that this sequence does not belong to A, i.e. s1(T) lost.
- Consider the strategy {s2(T)} of the second player.
- Go through the next entire game, generating (together with the second player's strategy s2(T)) a sequence {c(1), d(2), c(3), d(4),...,c(t), d(t+1),...}, making sure that this sequence is different from {a(1), b(2), a(3), b(4),...,a(t), b(t+1),...}.
- Decide that this sequence belongs to A, i.e. s2(T) lost.
- Keep repeating with further strategies if there are any, making sure that sequences already considered do not become generated again. (We start from the set of all sequences and each time we generate a sequence and refute a strategy we project the generated sequence onto first player moves and onto second player moves, and we take away the two resulting sequences from our set of sequences.)
- For all sequences that did not come up in the above consideration arbitrarily decide whether they belong to A, or to the complement of A.
Once this has been done we have a game G. If you give me a strategy s1 then we considered that strategy at some time T = T(s1). At time T, we decided an outcome of s1 that would be a loss of s1. Hence this strategy fails. But this is true for an arbitrary strategy; hence the axiom of determinacy and the axiom of choice are incompatible.
Infinite logic and the axiom of determinacy
Many different versions of infinitary logicInfinitary logic
An infinitary logic is a logic that allows infinitely long statements and/or infinitely long proofs. Some infinitary logics may have different properties from those of standard first-order logic. In particular, infinitary logics may fail to be compact or complete. Notions of compactness and...
were proposed in the late 20th century. One reason that has been given for believing in the axiom of determinacy is that it can be written as follows (in a version of infinite logic):
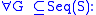
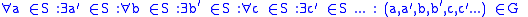 OR
OR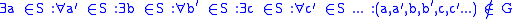
Note: Seq(S) is the set of all
 -sequences of S. The sentences here are infinitely long with a countably infinite list of quantifiers where the ellipses appear.
-sequences of S. The sentences here are infinitely long with a countably infinite list of quantifiers where the ellipses appear.In an infinitary logic, this principle is therefore a natural generalization of the usual (de Morgan) rule for quantifiers that
are true for finite formulas, such as
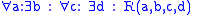 OR
OR 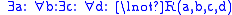 .
.Large cardinals and the axiom of determinacy
The consistency of the axiom of determinacy is closely related to the question of the consistency of large cardinal axioms. By a theorem of WoodinW. Hugh Woodin
William Hugh Woodin is an American mathematician and set theorist at University of California, Berkeley. He has made many notable contributions to the theory of inner models and determinacy. A type of large cardinal, the Woodin cardinal, bears his name.-Biography:Born in Tucson, Arizona, Woodin...
, the consistency of Zermelo–Fraenkel set theory without choice (ZF) together with the axiom of determinacy is equivalent to the consistency of Zermelo–Fraenkel set theory with choice (ZFC) together with the existence of infinitely many Woodin cardinal
Woodin cardinal
In set theory, a Woodin cardinal is a cardinal number λ such that for all functionsthere exists a cardinal κ In set theory, a Woodin cardinal is a cardinal number λ such that for all functions...
s. Since Woodin cardinals are strongly inaccessible
Inaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
, if AD is consistent, then so are an infinity of inaccessible cardinals.
Moreover, if to the hypothesis of an infinite set of Woodin cardinals is added the existence of a measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
larger than all of them, a very strong theory of Lebesgue measurable sets of reals emerges, as it is then provable that the axiom of determinacy is true in L(R)
L(R)
In set theory, L is the smallest transitive inner model of ZF containing all the ordinals and all the reals. It can be constructed in a manner analogous to the construction of L , by adding in all the reals at the start, and then iterating the definable powerset operation through all the...
, and therefore that every set of real numbers in L(R) is determined.
See also
- Axiom of real determinacyAxiom of real determinacyIn mathematics, the axiom of real determinacy is an axiom in set theory. It states the following:The axiom of real determinacy is a stronger version of the axiom of determinacy, which makes the same statement about games where both players choose integers; it is inconsistent with the axiom of choice...
(ADR) - AD+, a variant of the axiom of determinacy formulated by Woodin
- Axiom of quasi-determinacy (ADQ)
Further reading
- Philipp Rohde, On Extensions of the Axiom of Determinacy, Thesis, Department of Mathematics, University of Bonn, Germany, 2001
- Søren Riis, A Fractal which violates the Axiom of Determinacy, BRICS-94-24, available online
- Telgársky, R.J. Topological Games: On the 50th Anniversary of the Banach-Mazur Game, Rocky Mountain J. Math. 17 (1987), pp. 227–276.http://telgarska.com/1987-RMJM-Telgarsky-Topological-Games.pdf (3.19 MB)

