Order theory
Encyclopedia
Order theory is a branch of mathematics
which investigates our intuitive notion of order using binary relation
s. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions. A list of order-theoretic terms can be found in the order theory glossary.
. The first order often discussed in primary school is the standard order on the natural numbers e.g. "2 is less than 3", "10 is greater than 5", or "Does Tom have fewer cookies than Sally?". This intuitive concept can be extended to orders on other sets of number
s, such as the integer
s and the reals
. The idea of being greater than or less than another number is one of the basic intuitions of number systems (compare with numeral systems) in general (although one usually is also interested in the actual difference
of two numbers, which is not given by the order). Another familiar example of an ordering is the lexicographic order of words in a dictionary.
The above types of orders have a special property: each element can be compared to any other element, i.e. it is greater, smaller, or equal. However, this is not always a desired requirement. For example, consider the subset
ordering of sets. If a set A contains all the elements of a set B, then B is said to be smaller than or equal to A. Yet there are some sets that cannot be related in this fashion. Whenever both contain some elements that are not in the other, the two sets are not related by subset-inclusion. Hence, subset-inclusion is only a partial order, as opposed to the total orders
given before.
Order theory captures the intuition of orders that arises from such examples in a general setting. This is achieved by specifying properties that a relation ≤ must have to be a mathematical order. This more abstract approach makes much sense, because one can derive numerous theorems in the general setting, without focusing on the details of any particular order. These insights can then be readily transferred to many less abstract applications.
Driven by the wide practical usage of orders, numerous special kinds of ordered sets have been defined, some of which have grown into mathematical fields of their own. In addition, order theory does not restrict itself to the various classes of ordering relations, but also considers appropriate functions
between them. A simple example of an order theoretic property for functions comes from analysis
where monotone
functions are frequently found.
, arithmetic
, and binary relation
s.
, antisymmetric
, and transitive
, i.e., for all a, b and c in P, we have that:
A set with a partial order
on it is called a partially ordered set, poset, or just an ordered set if the intended meaning is clear. By checking these properties, one immediately sees that the well-known orders on natural number
s, integer
s, rational number
s and reals
are all orders in the above sense. However, they have the additional property of being total
, i.e., for all a and b in P, we have that:
These orders can also be called linear orders or chains. While many classical orders are linear, the subset
order on sets provides an example where this is not the case. Another example is given by the divisibility relation "|". For two natural numbers n and m, we write n|m if n divides
m without remainder. One easily sees that this yields a partial order.
The identity relation = on any set is also a partial order in which every two distinct elements are incomparable. It is also the only relation that is both a partial order and an equivalence relation
. Many advanced properties of posets are interesting mainly for non-linear orders.
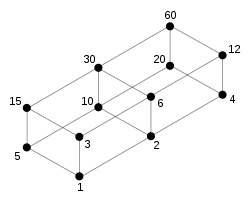Hasse diagram
s can visually represent the elements and relations of a partial ordering. These are graph drawing
s where the vertices
are the elements of the poset and the ordering relation is indicated by both the edges
and the relative positioning of the vertices. Orders are drawn bottom-up: if an element x is smaller than (precedes) y then there exists a path from x to y that is directed upwards. It is often necessary for the edges connecting elements to cross each other, but elements must never be located within an edge. An instructive exercise is to draw the Hasse diagram for the set of natural numbers that are smaller than or equal to 13, ordered by | (the divides
relation).
Even some infinite sets can be diagrammed by superimposing an ellipsis
(...) on a finite sub-order. This works well for the natural numbers, but it fails for the reals, where there is no immediate successor above 0. However, quite often one can obtain an intuition related to diagrams of a similar kind.
is the least set under the subset order. Formally, an element m is a least element if:
The notation 0 is frequently found for the least element, even when no numbers are concerned. However, in orders on sets of numbers, this notation might be inappropriate or ambiguous, since the number 0 is not always least. An example is given by the above divisibility order |, where 1 is the least element since it divides all other numbers. In contrast, 0 is the number that is divided by all other numbers. Hence it is the greatest element of the order. Other frequent terms for the least and greatest elements is bottom and top or zero and unit.
Least and greatest element
s may fail to exist, as the example of the real numbers shows. But if they exist, they are always unique. In contrast, consider the divisibility relation | on the set {2,3,4,5,6}. Although this set has neither top nor bottom, the elements 2, 3, and 5 have no elements below them, while 4, 5, and 6 have none above. Such elements are called minimal and maximal, respectively. Formally, an element m is minimal if:
Exchanging ≤ with ≥ yields the definition of maximality
. As the example shows, there can be many maximal elements and some elements may be both maximal and minimal (e.g. 5 above). However, if there is a least element, then it is the only minimal element of the order. Again, in infinite posets maximal elements do not always exist - the set of all finite subsets of a given infinite set, ordered by subset inclusion, provides one of many counterexamples. An important tool to ensure the existence of maximal elements under certain conditions is Zorn's Lemma
.
Subsets of partially ordered sets inherit the order. We already applied this by considering the subset {2,3,4,5,6} of the natural numbers with the induced divisibility ordering. Now there are also elements of a poset that are special with respect to some subset of the order. This leads to the definition of upper bound
s. Given a subset S of some poset P, an upper bound of S is an element b of P that is above all elements of S. Formally, this means that
Lower bounds again are defined by inverting the order. For example, -5 is a lower bound of the natural numbers as a subset of the integers. Given a set of sets, an upper bound for these sets under the subset ordering is given by their union
. In fact, this upper bound is quite special: it is the smallest set that contains all of the sets. Hence, we have found the least upper bound of a set of sets. This concept is also called supremum or join, and for a set S one writes sup(S) or vS for its least upper bound. Conversely, the greatest lower bound is known as infimum
or meet and denoted inf(S) or ^S. These concepts play an important role in many applications of order theory. For two elements x and y, one also writes x v y and x ^ y for sup({x,y}) and inf({x,y}), respectively.
For another example, consider again the relation | on natural numbers. The least upper bound of two numbers is the smallest number that is divided by both of them, i.e. the least common multiple
of the numbers. Greatest lower bounds in turn are given by the greatest common divisor
.
Every order theoretic definition has its dual: it is the notion one obtains by applying the definition to the inverse order. Since all concepts are symmetric, this operation preserves the theorems of partial orders. For a given mathematical result, one can just invert the order and replace all definitions by their duals and one obtains another valid theorem. This is important and useful, since one obtains two theorems for the price of one. Some more details and examples can be found in the article on duality in order theory
.
of two partially ordered sets, taken together with the product order
on pairs of elements. The ordering is defined by (a, x) ≤ (b, y) if (and only if) a ≤ b and x ≤ y. (Notice carefully that there are three distinct meanings for the relation symbol ≤ in this definition.) The disjoint union
of two posets is another typical example of order construction, where the order is just the (disjoint) union of the original orders.
Every partial order ≤ gives rise to a so-called strict order <, by defining a < b if a ≤ b and not b ≤ a. This transformation can be inverted by setting a ≤ b if a < b or a = b. The two concepts are equivalent although in some circumstances one can be more convenient to work with than the other.
. A function f from a poset P to a poset Q is monotone, or order-preserving, if a ≤ b in P implies f(a) ≤ f(b) in Q (Noting that, strictly, the two relations here are different since they apply to different sets.). The converse of this implication leads to functions that are order-reflecting, i.e. functions f as above for which f(a) ≤ f(b) implies a ≤ b. On the other hand, a function may also be order-reversing or antitone, if a ≤ b implies f(b) ≤ f(a).
An order-embedding
is a function f between orders that is both order-preserving and order-reflecting. Examples for these definitions are found easily. For instance, the function that maps a natural number to its successor is clearly monotone with respect to the natural order. Any function from a discrete order, i.e. from a set ordered by the identity order "=", is also monotone. Mapping each natural number to the corresponding real number gives an example for an order embedding. The set complement
on a powerset is an example of an antitone function.
An important question is when two orders are "essentially equal", i.e. when they are the same up to renaming of elements. Order isomorphism
s are functions that define such a renaming. An order-isomorphism is a monotone bijective function that has a monotone inverse. This is equivalent to being a surjective order-embedding. Hence, the image f(P) of an order-embedding is always isomorphic to P, which justifies the term "embedding".
A more elaborate type of functions is given by so-called Galois connection
s. Monotone Galois connections can be viewed as a generalization of order-isomorphisms, since they constitute of a pair of two functions in converse directions, which are "not quite" inverse to each other, but that still have close relationships.
Another special type of self-maps on a poset are closure operator
s, which are not only monotonic, but also idempotent, i.e. f(x) = f(f(x)), and extensive (or inflationary), i.e. x ≤ f(x). These have many applications in all kinds of "closures" that appear in mathematics.
Besides being compatible with the mere order relations, functions between posets may also behave well with respect to special elements and constructions. For example, when talking about posets with least element, it may seem reasonable to consider only monotonic functions that preserve this element, i.e. which map least elements to least elements. If binary infima ^ exist, then a reasonable property might be to require that f(x^y) = f(x)^f(y), for all x and y. All of these properties, and indeed many more, may be compiled under the label of limit-preserving functions
.
Finally, one can invert the view, switching from functions of orders to orders of functions. Indeed, the functions between two posets P and Q can be ordered via the pointwise order. For two functions f and g, we have f ≤ g if f(x) ≤ g(x) for all elements x of P. This occurs for example in domain theory
, where function space
s play an important role.
has to be mentioned. A preorder is a relation that is reflexive and transitive, but not necessarily antisymmetric. Each preorder induces an equivalence relation
between elements, where a is equivalent to b, if a ≤ b and b ≤ a. Preorders can be turned into orders by identifying all elements that are equivalent with respect to this relation.
Several types of orders can be defined from numerical data on the items of the order: a total order
results from attaching distinct real numbers to each item and using the numerical comparisons to order the items; instead, if distinct items are allowed to have equal numerical scores, one obtains a strict weak ordering
. Requiring two scores to be separated by a fixed threshold before they may be compared leads to the concept of a semiorder
, while allowing the threshold to vary on a per-item basis produces an interval order
.
An additional simple but useful property leads to so-called well-order
s, for which all non-empty subsets have a minimal element. Generalizing well-orders from linear to partial orders, a set is well partially ordered if all its non-empty subsets have a finite number of minimal elements.
Many other types of orders arise when the existence of infima
and suprema
of certain sets is guaranteed. Focusing on this aspect, usually referred to as completeness
of orders, one obtains:
However, one can go even further: if all finite non-empty infima exist, then ^ can be viewed as a total binary operation in the sense of universal algebra
. Hence, in a lattice, two operations ^ and v are available, and one can define new properties by giving identities, such as
This condition is called distributivity and gives rise to distributive lattice
s. There are some other important distributivity laws which are discussed in the article on distributivity in order theory
. Some additional order structures that are often specified via algebraic operations and defining identities are
which both introduce a new operation ~ called negation. Both structures play a role in mathematical logic
and especially Boolean algebras have major applications in computer science
.
Finally, various structures in mathematics combine orders with even more algebraic operations, as in the case of quantale
s, that allow for the definition of an addition operation.
Many other important properties of posets exist. For example, a poset is locally finite if every closed interval
[a, b] in it is finite. Locally finite posets give rise to incidence algebra
s which in turn can be used to define the Euler characteristic of finite bounded posets.
More complicated lower subsets are ideals
, which have the additional property that each two of their elements have an upper bound within the ideal. Their duals are given by filters
. A related concept is that of a directed subset
, which like an ideal contains upper bounds of finite subsets, but does not have to be a lower set. Furthermore it is often generalized to preordered sets.
A subset which is - as a sub-poset - linearly ordered, is called a chain. The opposite notion, the antichain
, is a subset that contains no two comparable elements; i.e. that is a discrete order.
are an important tool for many order theoretic considerations. Beside formalizing orders in terms of algebraic structures that satisfy certain identities, one can also establish other connections to algebra. An example is given by the correspondence between Boolean algebras and Boolean ring
s. Other issues are concerned with the existence of free constructions, such as free lattices based on a given set of generators. Furthermore, closure operators are important in the study of universal algebra.
orders play a very prominent role. In fact, the set of open set
s provides a classical example of a complete lattice, more precisely a complete Heyting algebra
(or "frame" or "locale"). Filters
and nets
are notions closely related to order theory and the closure operator of sets
can be used to define topology. Beyond these relations, topology can be looked at solely in terms of the open set lattices, which leads to the study of pointless topology
. Furthermore, a natural preorder of elements of the underlying set of a topology is given by the so-called specialization order, that is actually a partial order if the topology is T0.
Conversely, in order theory, one often makes use of topological results. There are various ways to define subsets of an order which can be considered as open sets of a topology. Especially, it is interesting to consider topologies on a poset (X, ≤) that in turn induce ≤ as their specialization order. The finest such topology is the Alexandrov topology
, given by taking all upper sets as opens. Conversely, the coarsest topology that induces the specialization order is the upper topology, having the complements of principal ideals
(i.e. sets of the form {y in X | y ≤ x} for some x) as a subbase
. Additionally, a topology with specialization order ≤ may be order consistent, meaning that their open sets are "inaccessible by directed suprema" (with respect to ≤). The finest order consistent topology is the Scott topology, which is coarser than the Alexandrov topology. A third important topology in this spirit is the Lawson topology
. There are close connections between these topologies and the concepts of order theory. For example, a function preserves directed suprema iff
it is continuous with respect to the Scott topology (for this reason this order theoretic property is also called Scott-continuity).
, where the nodes are the elements of the poset and there is a directed path from a to b if and only if a ≤ b. Dropping the requirement of being acyclic, one can also obtain all preorders.
When equipped with all transitive edges, these graphs in turn are just special categories
, where elements are objects and each set of morphisms between two elements is at most singleton. Functions between orders become functors between categories. Interestingly, many ideas of order theory are just concepts of category theory in small. For example, a supremum is just a categorical product
. More generally, one can capture suprema and infima under the abstract notion of a categorical limit
(or colimit, respectively). Another place where categorical ideas occur is the concept of a (monotone) Galois connection
, which is just the same as a pair of adjoint functors.
But category theory also has its impact on order theory on a larger scale. Classes of posets with appropriate functions as discussed above form interesting categories. Often one can also state constructions of orders, like the product order
, in terms of categories. Further insights result when categories of orders are found categorically equivalent
to other categories, for example of topological spaces. This line of research leads to various representation theorems, often collected under the label of Stone duality
.
are of great importance. Moreover, works of Charles Sanders Peirce, Richard Dedekind
, and Ernst Schröder
also consider concepts of order theory. Certainly, there are others to be named in this context and surely there exists more detailed material on the history of order theory.
The term poset as an abbreviation for partially ordered set was coined by Garrett Birkhoff
in the second edition of his influential book Lattice Theory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
which investigates our intuitive notion of order using binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions. A list of order-theoretic terms can be found in the order theory glossary.
Background and motivation
Orders are everywhere in mathematics and related fields like computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. The first order often discussed in primary school is the standard order on the natural numbers e.g. "2 is less than 3", "10 is greater than 5", or "Does Tom have fewer cookies than Sally?". This intuitive concept can be extended to orders on other sets of number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s, such as the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. The idea of being greater than or less than another number is one of the basic intuitions of number systems (compare with numeral systems) in general (although one usually is also interested in the actual difference
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
of two numbers, which is not given by the order). Another familiar example of an ordering is the lexicographic order of words in a dictionary.
The above types of orders have a special property: each element can be compared to any other element, i.e. it is greater, smaller, or equal. However, this is not always a desired requirement. For example, consider the subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
ordering of sets. If a set A contains all the elements of a set B, then B is said to be smaller than or equal to A. Yet there are some sets that cannot be related in this fashion. Whenever both contain some elements that are not in the other, the two sets are not related by subset-inclusion. Hence, subset-inclusion is only a partial order, as opposed to the total orders
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
given before.
Order theory captures the intuition of orders that arises from such examples in a general setting. This is achieved by specifying properties that a relation ≤ must have to be a mathematical order. This more abstract approach makes much sense, because one can derive numerous theorems in the general setting, without focusing on the details of any particular order. These insights can then be readily transferred to many less abstract applications.
Driven by the wide practical usage of orders, numerous special kinds of ordered sets have been defined, some of which have grown into mathematical fields of their own. In addition, order theory does not restrict itself to the various classes of ordering relations, but also considers appropriate functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
between them. A simple example of an order theoretic property for functions comes from analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
where monotone
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
functions are frequently found.
Basic definitions
This section introduces ordered sets by building upon the concepts of set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, and binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s.
Partially ordered sets
Orders are special binary relations. Suppose that P is a set and that ≤ is a relation on P. Then ≤ is a partial order if it is reflexiveReflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, antisymmetric
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
, and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, i.e., for all a, b and c in P, we have that:
- a ≤ a (reflexivity)
- if a ≤ b and b ≤ a then a = b (antisymmetry)
- if a ≤ b and b ≤ c then a ≤ c (transitivity).
A set with a partial order
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
on it is called a partially ordered set, poset, or just an ordered set if the intended meaning is clear. By checking these properties, one immediately sees that the well-known orders on natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s and reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
are all orders in the above sense. However, they have the additional property of being total
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
, i.e., for all a and b in P, we have that:
- a ≤ b or b ≤ a (totality).
These orders can also be called linear orders or chains. While many classical orders are linear, the subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
order on sets provides an example where this is not the case. Another example is given by the divisibility relation "|". For two natural numbers n and m, we write n|m if n divides
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
m without remainder. One easily sees that this yields a partial order.
The identity relation = on any set is also a partial order in which every two distinct elements are incomparable. It is also the only relation that is both a partial order and an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
. Many advanced properties of posets are interesting mainly for non-linear orders.
Visualizing a poset
Hasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
s can visually represent the elements and relations of a partial ordering. These are graph drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
s where the vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
are the elements of the poset and the ordering relation is indicated by both the edges
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
and the relative positioning of the vertices. Orders are drawn bottom-up: if an element x is smaller than (precedes) y then there exists a path from x to y that is directed upwards. It is often necessary for the edges connecting elements to cross each other, but elements must never be located within an edge. An instructive exercise is to draw the Hasse diagram for the set of natural numbers that are smaller than or equal to 13, ordered by | (the divides
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
relation).
Even some infinite sets can be diagrammed by superimposing an ellipsis
Ellipsis
Ellipsis is a series of marks that usually indicate an intentional omission of a word, sentence or whole section from the original text being quoted. An ellipsis can also be used to indicate an unfinished thought or, at the end of a sentence, a trailing off into silence...
(...) on a finite sub-order. This works well for the natural numbers, but it fails for the reals, where there is no immediate successor above 0. However, quite often one can obtain an intuition related to diagrams of a similar kind.
Special elements within an order
In a partially ordered set there may be some elements that play a special role. The most basic example is given by the least element of a poset. For example, 1 is the least element of the positive integers and the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is the least set under the subset order. Formally, an element m is a least element if:
- m ≤ a, for all elements a of the order.
The notation 0 is frequently found for the least element, even when no numbers are concerned. However, in orders on sets of numbers, this notation might be inappropriate or ambiguous, since the number 0 is not always least. An example is given by the above divisibility order |, where 1 is the least element since it divides all other numbers. In contrast, 0 is the number that is divided by all other numbers. Hence it is the greatest element of the order. Other frequent terms for the least and greatest elements is bottom and top or zero and unit.
Least and greatest element
Greatest element
In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
s may fail to exist, as the example of the real numbers shows. But if they exist, they are always unique. In contrast, consider the divisibility relation | on the set {2,3,4,5,6}. Although this set has neither top nor bottom, the elements 2, 3, and 5 have no elements below them, while 4, 5, and 6 have none above. Such elements are called minimal and maximal, respectively. Formally, an element m is minimal if:
- a ≤ m implies a = m, for all elements a of the order.
Exchanging ≤ with ≥ yields the definition of maximality
Maximal element
In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
. As the example shows, there can be many maximal elements and some elements may be both maximal and minimal (e.g. 5 above). However, if there is a least element, then it is the only minimal element of the order. Again, in infinite posets maximal elements do not always exist - the set of all finite subsets of a given infinite set, ordered by subset inclusion, provides one of many counterexamples. An important tool to ensure the existence of maximal elements under certain conditions is Zorn's Lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
.
Subsets of partially ordered sets inherit the order. We already applied this by considering the subset {2,3,4,5,6} of the natural numbers with the induced divisibility ordering. Now there are also elements of a poset that are special with respect to some subset of the order. This leads to the definition of upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
s. Given a subset S of some poset P, an upper bound of S is an element b of P that is above all elements of S. Formally, this means that
- s ≤ b, for all s in S.
Lower bounds again are defined by inverting the order. For example, -5 is a lower bound of the natural numbers as a subset of the integers. Given a set of sets, an upper bound for these sets under the subset ordering is given by their union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
. In fact, this upper bound is quite special: it is the smallest set that contains all of the sets. Hence, we have found the least upper bound of a set of sets. This concept is also called supremum or join, and for a set S one writes sup(S) or vS for its least upper bound. Conversely, the greatest lower bound is known as infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
or meet and denoted inf(S) or ^S. These concepts play an important role in many applications of order theory. For two elements x and y, one also writes x v y and x ^ y for sup({x,y}) and inf({x,y}), respectively.
For another example, consider again the relation | on natural numbers. The least upper bound of two numbers is the smallest number that is divided by both of them, i.e. the least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
of the numbers. Greatest lower bounds in turn are given by the greatest common divisor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
.
Duality
In the previous definitions, we often noted that a concept can be defined by just inverting the ordering in a former definition. This is the case for "least" and "greatest", for "minimal" and "maximal", for "upper bound" and "lower bound", and so on. This is a general situation in order theory: A given order can be inverted by just exchanging its direction, pictorially flipping the Hasse diagram top-down. This yields the so-called dual, inverse, or opposite order.Every order theoretic definition has its dual: it is the notion one obtains by applying the definition to the inverse order. Since all concepts are symmetric, this operation preserves the theorems of partial orders. For a given mathematical result, one can just invert the order and replace all definitions by their duals and one obtains another valid theorem. This is important and useful, since one obtains two theorems for the price of one. Some more details and examples can be found in the article on duality in order theory
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
.
Constructing new orders
There are many ways to construct orders out of given orders. The dual order is one example. Another important construction is the cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of two partially ordered sets, taken together with the product order
Product order
In mathematics, given two ordered sets A and B, one can induce a partial ordering on the Cartesian product A × B. Giventwo pairs and in A × B, one sets ≤...
on pairs of elements. The ordering is defined by (a, x) ≤ (b, y) if (and only if) a ≤ b and x ≤ y. (Notice carefully that there are three distinct meanings for the relation symbol ≤ in this definition.) The disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of two posets is another typical example of order construction, where the order is just the (disjoint) union of the original orders.
Every partial order ≤ gives rise to a so-called strict order <, by defining a < b if a ≤ b and not b ≤ a. This transformation can be inverted by setting a ≤ b if a < b or a = b. The two concepts are equivalent although in some circumstances one can be more convenient to work with than the other.
Functions between orders
It is reasonable to consider functions between partially ordered sets having certain additional properties that are related to the ordering relations of the two sets. The most fundamental condition that occurs in this context is monotonicityMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
. A function f from a poset P to a poset Q is monotone, or order-preserving, if a ≤ b in P implies f(a) ≤ f(b) in Q (Noting that, strictly, the two relations here are different since they apply to different sets.). The converse of this implication leads to functions that are order-reflecting, i.e. functions f as above for which f(a) ≤ f(b) implies a ≤ b. On the other hand, a function may also be order-reversing or antitone, if a ≤ b implies f(b) ≤ f(a).
An order-embedding
Order-embedding
In mathematical order theory, an order-embedding is a special kind of monotone function, which provides a way to include one partially ordered set into another. Like Galois connections, order-embeddings constitute a notion which is strictly weaker than the concept of an order isomorphism...
is a function f between orders that is both order-preserving and order-reflecting. Examples for these definitions are found easily. For instance, the function that maps a natural number to its successor is clearly monotone with respect to the natural order. Any function from a discrete order, i.e. from a set ordered by the identity order "=", is also monotone. Mapping each natural number to the corresponding real number gives an example for an order embedding. The set complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
on a powerset is an example of an antitone function.
An important question is when two orders are "essentially equal", i.e. when they are the same up to renaming of elements. Order isomorphism
Order isomorphism
In the mathematical field of order theory an order isomorphism is a special kind of monotone function that constitutes a suitable notion of isomorphism for partially ordered sets . Whenever two posets are order isomorphic, they can be considered to be "essentially the same" in the sense that one of...
s are functions that define such a renaming. An order-isomorphism is a monotone bijective function that has a monotone inverse. This is equivalent to being a surjective order-embedding. Hence, the image f(P) of an order-embedding is always isomorphic to P, which justifies the term "embedding".
A more elaborate type of functions is given by so-called Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
s. Monotone Galois connections can be viewed as a generalization of order-isomorphisms, since they constitute of a pair of two functions in converse directions, which are "not quite" inverse to each other, but that still have close relationships.
Another special type of self-maps on a poset are closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
s, which are not only monotonic, but also idempotent, i.e. f(x) = f(f(x)), and extensive (or inflationary), i.e. x ≤ f(x). These have many applications in all kinds of "closures" that appear in mathematics.
Besides being compatible with the mere order relations, functions between posets may also behave well with respect to special elements and constructions. For example, when talking about posets with least element, it may seem reasonable to consider only monotonic functions that preserve this element, i.e. which map least elements to least elements. If binary infima ^ exist, then a reasonable property might be to require that f(x^y) = f(x)^f(y), for all x and y. All of these properties, and indeed many more, may be compiled under the label of limit-preserving functions
Limit-preserving function (order theory)
In the mathematical area of order theory, one often speaks about functions that preserve certain limits, i.e. certain suprema or infima. Roughly speaking, these functions map the supremum/infimum of a set to the supremum/infimum of the image of the set...
.
Finally, one can invert the view, switching from functions of orders to orders of functions. Indeed, the functions between two posets P and Q can be ordered via the pointwise order. For two functions f and g, we have f ≤ g if f(x) ≤ g(x) for all elements x of P. This occurs for example in domain theory
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
, where function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s play an important role.
Special types of orders
Many of the structures that are studied in order theory employ order relations with further properties. In fact, even some relations that are not partial orders are of special interest. Mainly the concept of a preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
has to be mentioned. A preorder is a relation that is reflexive and transitive, but not necessarily antisymmetric. Each preorder induces an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
between elements, where a is equivalent to b, if a ≤ b and b ≤ a. Preorders can be turned into orders by identifying all elements that are equivalent with respect to this relation.
Several types of orders can be defined from numerical data on the items of the order: a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
results from attaching distinct real numbers to each item and using the numerical comparisons to order the items; instead, if distinct items are allowed to have equal numerical scores, one obtains a strict weak ordering
Strict weak ordering
In mathematics, especially order theory, a strict weak ordering is a binary relation In mathematics, especially order theory, a strict weak ordering is a binary relation ...
. Requiring two scores to be separated by a fixed threshold before they may be compared leads to the concept of a semiorder
Semiorder
In order theory, a branch of mathematics, a semiorder is a type of ordering that may be determined for a set of items with numerical scores by declaring two items to be incomparable when their scores are within some threshold of each other and otherwise using the numerical comparison of their scores...
, while allowing the threshold to vary on a per-item basis produces an interval order
Interval order
In mathematics, especially order theory,the interval order for a collection of intervals on the real lineis the partial order corresponding to their left-to-right precedence relation—one interval, I1, being considered less than another, I2, if I1 is completely to the left of I2.More formally, a...
.
An additional simple but useful property leads to so-called well-order
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
s, for which all non-empty subsets have a minimal element. Generalizing well-orders from linear to partial orders, a set is well partially ordered if all its non-empty subsets have a finite number of minimal elements.
Many other types of orders arise when the existence of infima
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
and suprema
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of certain sets is guaranteed. Focusing on this aspect, usually referred to as completeness
Completeness (order theory)
In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...
of orders, one obtains:
- Bounded posets, i.e. posets with a least and greatest elementGreatest elementIn mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
(which are just the supremum and infimum of the empty subset), - LatticesLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, in which every non-empty finite set has a supremum and infimum, - Complete latticeComplete latticeIn mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
s, where every set has a supremum and infimum, and - Directed complete partial orders (dcpos), that guarantee the existence of suprema of all directed subsetsDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
and that are studied in domain theoryDomain theoryDomain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
.
However, one can go even further: if all finite non-empty infima exist, then ^ can be viewed as a total binary operation in the sense of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
. Hence, in a lattice, two operations ^ and v are available, and one can define new properties by giving identities, such as
- x ^ (y v z) = (x ^ y) v (x ^ z), for all x, y, and z.
This condition is called distributivity and gives rise to distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
s. There are some other important distributivity laws which are discussed in the article on distributivity in order theory
Distributivity (order theory)
In the mathematical area of order theory, there are various notions of the common concept of distributivity, applied to the formation of suprema and infima...
. Some additional order structures that are often specified via algebraic operations and defining identities are
- Heyting algebraHeyting algebraIn mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
s and - Boolean algebras,
which both introduce a new operation ~ called negation. Both structures play a role in mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and especially Boolean algebras have major applications in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.
Finally, various structures in mathematics combine orders with even more algebraic operations, as in the case of quantale
Quantale
In mathematics, quantales are certain partially ordered algebraic structures that generalize locales as well as various multiplicative lattices of ideals from ring theory and functional analysis...
s, that allow for the definition of an addition operation.
Many other important properties of posets exist. For example, a poset is locally finite if every closed interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a, b] in it is finite. Locally finite posets give rise to incidence algebra
Incidence algebra
In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
s which in turn can be used to define the Euler characteristic of finite bounded posets.
Subsets of ordered sets
In an ordered set, one can define many types of special subsets based on the given order. A simple example are upper sets; i.e. sets that contain all elements that are above them in the order. Formally, the upper closure of a set S in a poset P is given by the set {x in P | there is some y in S with y ≤ x}. A set that is equal to its upper closure is called an upper set. Lower sets are defined dually.More complicated lower subsets are ideals
Ideal (order theory)
In mathematical order theory, an ideal is a special subset of a partially ordered set . Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion...
, which have the additional property that each two of their elements have an upper bound within the ideal. Their duals are given by filters
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
. A related concept is that of a directed subset
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
, which like an ideal contains upper bounds of finite subsets, but does not have to be a lower set. Furthermore it is often generalized to preordered sets.
A subset which is - as a sub-poset - linearly ordered, is called a chain. The opposite notion, the antichain
Antichain
In mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
, is a subset that contains no two comparable elements; i.e. that is a discrete order.
Related mathematical areas
Although most mathematical areas use orders in one or the other way, there are also a few theories that have relationships which go far beyond mere application. Together with their major touching points with order theory, some of these are to be presented below.Universal algebra
As already mentioned, the methods and formalisms of universal algebraUniversal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
are an important tool for many order theoretic considerations. Beside formalizing orders in terms of algebraic structures that satisfy certain identities, one can also establish other connections to algebra. An example is given by the correspondence between Boolean algebras and Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
s. Other issues are concerned with the existence of free constructions, such as free lattices based on a given set of generators. Furthermore, closure operators are important in the study of universal algebra.
Topology
In topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
orders play a very prominent role. In fact, the set of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s provides a classical example of a complete lattice, more precisely a complete Heyting algebra
Heyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
(or "frame" or "locale"). Filters
Filter (mathematics)
In mathematics, a filter is a special subset of a partially ordered set. A frequently used special case is the situation that the ordered set under consideration is just the power set of some set, ordered by set inclusion. Filters appear in order and lattice theory, but can also be found in...
and nets
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
are notions closely related to order theory and the closure operator of sets
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
can be used to define topology. Beyond these relations, topology can be looked at solely in terms of the open set lattices, which leads to the study of pointless topology
Pointless topology
In mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
. Furthermore, a natural preorder of elements of the underlying set of a topology is given by the so-called specialization order, that is actually a partial order if the topology is T0.
Conversely, in order theory, one often makes use of topological results. There are various ways to define subsets of an order which can be considered as open sets of a topology. Especially, it is interesting to consider topologies on a poset (X, ≤) that in turn induce ≤ as their specialization order. The finest such topology is the Alexandrov topology
Alexandrov topology
In topology, an Alexandrov space is a topological space in which the intersection of any family of open sets is open. It is an axiom of topology that the intersection of any finite family of open sets is open...
, given by taking all upper sets as opens. Conversely, the coarsest topology that induces the specialization order is the upper topology, having the complements of principal ideals
Ideal (order theory)
In mathematical order theory, an ideal is a special subset of a partially ordered set . Although this term historically was derived from the notion of a ring ideal of abstract algebra, it has subsequently been generalized to a different notion...
(i.e. sets of the form {y in X | y ≤ x} for some x) as a subbase
Subbase
In topology, a subbase for a topological space X with topology T is a subcollection B of T which generates T, in the sense that T is the smallest topology containing B...
. Additionally, a topology with specialization order ≤ may be order consistent, meaning that their open sets are "inaccessible by directed suprema" (with respect to ≤). The finest order consistent topology is the Scott topology, which is coarser than the Alexandrov topology. A third important topology in this spirit is the Lawson topology
Lawson topology
In mathematics and theoretical computer science the Lawson topology, named after J. D. Lawson, is a topology on partially ordered sets used in the study of domain theory. The lower topology on a poset P is generated by the subbasis consisting of all complements of principal filters on P...
. There are close connections between these topologies and the concepts of order theory. For example, a function preserves directed suprema iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
it is continuous with respect to the Scott topology (for this reason this order theoretic property is also called Scott-continuity).
Category theory
The visualization of orders with Hasse diagrams has a straightforward generalization: instead of displaying lesser elements below greater ones, the direction of the order can also be depicted by giving directions to the edges of a graph. In this way, each order is seen to be equivalent to a directed acyclic graphDirected acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
, where the nodes are the elements of the poset and there is a directed path from a to b if and only if a ≤ b. Dropping the requirement of being acyclic, one can also obtain all preorders.
When equipped with all transitive edges, these graphs in turn are just special categories
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, where elements are objects and each set of morphisms between two elements is at most singleton. Functions between orders become functors between categories. Interestingly, many ideas of order theory are just concepts of category theory in small. For example, a supremum is just a categorical product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
. More generally, one can capture suprema and infima under the abstract notion of a categorical limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
(or colimit, respectively). Another place where categorical ideas occur is the concept of a (monotone) Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
, which is just the same as a pair of adjoint functors.
But category theory also has its impact on order theory on a larger scale. Classes of posets with appropriate functions as discussed above form interesting categories. Often one can also state constructions of orders, like the product order
Product order
In mathematics, given two ordered sets A and B, one can induce a partial ordering on the Cartesian product A × B. Giventwo pairs and in A × B, one sets ≤...
, in terms of categories. Further insights result when categories of orders are found categorically equivalent
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
to other categories, for example of topological spaces. This line of research leads to various representation theorems, often collected under the label of Stone duality
Stone duality
In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation...
.
History
As explained before, orders are ubiquitous in mathematics. However, earliest explicit mentionings of partial orders are probably to be found not before the 19th century. In this context the works of George BooleGeorge Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
are of great importance. Moreover, works of Charles Sanders Peirce, Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, and Ernst Schröder
Ernst Schröder
Ernst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...
also consider concepts of order theory. Certainly, there are others to be named in this context and surely there exists more detailed material on the history of order theory.
The term poset as an abbreviation for partially ordered set was coined by Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
in the second edition of his influential book Lattice Theory.
See also
- Cyclic order
- HierarchyHierarchyA hierarchy is an arrangement of items in which the items are represented as being "above," "below," or "at the same level as" one another...
- Incidence algebraIncidence algebraIn order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
- Important publications in order theory
- Causal SetsCausal setsThe causal sets programme is an approach to quantum gravity. Its founding principle is that spacetime is fundamentally discrete and that the spacetime events are related by a partial order...
External links
- Orders at ProvenMath partial order, linear order, well order, initial segment; formal definitions and proofs within the axioms of set theory.