
Borel set
Encyclopedia
In mathematics
, a Borel set is any set in a topological space
that can be formed from open set
s (or, equivalently, from closed set
s) through the operations of countable union
, countable intersection
, and relative complement. Borel sets are named after Émile Borel
.
For a topological space X, the collection of all Borel sets on X forms a σ-algebra
, known as the Borel algebra or Borel σ-algebra
. The Borel algebra on X is
the smallest σ-algebra containing all open sets (or, equivalently, all closed sets).
Borel sets are important in measure theory, since any measure defined on the open sets of a space, or on the closed sets of a space, must also be defined on all Borel sets of that space. Any measure defined on the Borel sets is called a Borel measure. Borel sets and the associated Borel hierarchy
also play a fundamental role in descriptive set theory
.
In some contexts, Borel sets are defined to be generated by the compact sets of the topological space, rather than the open sets. The two definitions are equivalent for many well-behaved
spaces, including all Hausdorff
σ-compact spaces, but can be different in more pathological
spaces.
For a collection T of subsets of X (that is, for any subset of the power set P(X) of X), let
Now define by transfinite induction
a sequence Gm, where m is an ordinal number
, in the following manner:
We now claim that the Borel algebra is Gω1, where ω1 is the first uncountable ordinal number
. That is, the Borel algebra can be generated from the class of open sets by iterating the operation

to the first uncountable ordinal.
To prove this fact, note that any open set in a metric space is the union of an increasing sequence of closed sets. In particular, it is easy to show that complementation of sets maps Gm into itself for any limit ordinal m; moreover if m is an uncountable limit ordinal, Gm is closed under countable unions.
Note that for each Borel set B, there is some countable ordinal αB such that B can be obtained by iterating the operation over αB. However, as B varies over all Borel sets, αB will vary over all the countable ordinals, and thus the first ordinal at which all the Borel sets are obtained is ω1, the first uncountable ordinal.
, is the Borel algebra on the set of real number
s. It is the algebra on which the Borel measure is defined. Given a real random variable defined on a probability space
, its probability distribution
is by definition also a measure on the Borel algebra.
The Borel algebra on the reals is the smallest σ-algebra on R which contains all the intervals
.
In the construction by transfinite induction, it can be shown that, in each step, the number of sets is, at most, the power of the continuum. So, the total number of Borel sets is less than or equal to .
.
A Borel space is just another name for a set equipped with a distinguished σ-algebra; by extension elements of the distinguished σ-algebra are called Borel sets. Borel spaces form a category
in which the maps are Borel measurable mappings between Borel spaces, where

is Borel measurable means that f − 1(B) is Borel in X for any Borel subset B of Y.
Theorem. Let X be a Polish space
, that is, a topological space such that there is a metric
d on X which defines the topology of X and which makes X a complete separable metric space. Then X as a Borel space is isomorphic to one of
(1) R, (2) Z or (3) a finite space.
Considered as Borel spaces, the real line R and the union of R with a countable set are isomorphic.
A standard Borel space is the Borel space associated to a Polish space
.
Note that any standard Borel space is defined (up to isomorphism) by its cardinality, and any uncountable standard Borel space has the cardinality of the continuum.
For subsets of Polish spaces, Borel sets can be characterized as those sets which are the ranges of continuous injective maps defined on Polish spaces. Note however, that the range of a continuous noninjective map may fail to be Borel. See analytic set
.
Every probability measure
on a standard Borel space turns it into a standard probability space
.
, is described below. In contrast, an example of a non-measurable set
cannot be exhibited, though its existence can be proved.
Every irrational number
has a unique representation by a continued fraction
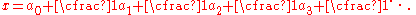
where is some integer
is some integer
and all the other numbers are positive integers. Let
are positive integers. Let 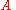 be the set of all irrational numbers that correspond to sequences
be the set of all irrational numbers that correspond to sequences  with the following property: there exists an infinite subsequence
with the following property: there exists an infinite subsequence
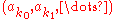 such that each element is a divisor
such that each element is a divisor
of the next element. This set is not Borel. In fact, it is analytic
is not Borel. In fact, it is analytic
, and complete in the class of analytic sets. For more details see descriptive set theory
and the book by Kechris
, especially Exercise (27.2) on page 209, Definition (22.9) on page 169, and Exercise (3.4)(ii) on page 14.
Another non-Borel set is an inverse image of an infinite parity function
of an infinite parity function  . However, this is a proof of existence (via the choice axiom), not an explicit example.
. However, this is a proof of existence (via the choice axiom), not an explicit example.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Borel set is any set in a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
that can be formed from open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s (or, equivalently, from closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s) through the operations of countable union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
, countable intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, and relative complement. Borel sets are named after Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
.
For a topological space X, the collection of all Borel sets on X forms a σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
, known as the Borel algebra or Borel σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
. The Borel algebra on X is
the smallest σ-algebra containing all open sets (or, equivalently, all closed sets).
Borel sets are important in measure theory, since any measure defined on the open sets of a space, or on the closed sets of a space, must also be defined on all Borel sets of that space. Any measure defined on the Borel sets is called a Borel measure. Borel sets and the associated Borel hierarchy
Borel hierarchy
In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...
also play a fundamental role in descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
.
In some contexts, Borel sets are defined to be generated by the compact sets of the topological space, rather than the open sets. The two definitions are equivalent for many well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
spaces, including all Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
σ-compact spaces, but can be different in more pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
spaces.
Generating the Borel algebra
In the case X is a metric space, the Borel algebra in the first sense may be described generatively as follows.For a collection T of subsets of X (that is, for any subset of the power set P(X) of X), let
-
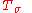 be all countable unions of elements of T
be all countable unions of elements of T -
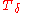 be all countable intersections of elements of T
be all countable intersections of elements of T -
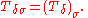
Now define by transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
a sequence Gm, where m is an ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
, in the following manner:
- For the base case of the definition,
 = the collection of open subsets of X.
= the collection of open subsets of X. - If i is not a limit ordinal, then i has an immediately preceding ordinal i − 1. Let
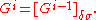
- If i is a limit ordinal, set

We now claim that the Borel algebra is Gω1, where ω1 is the first uncountable ordinal number
First uncountable ordinal
In mathematics, the first uncountable ordinal, traditionally denoted by ω1 or sometimes by Ω, is the smallest ordinal number that, considered as a set, is uncountable. It is the supremum of all countable ordinals...
. That is, the Borel algebra can be generated from the class of open sets by iterating the operation

to the first uncountable ordinal.
To prove this fact, note that any open set in a metric space is the union of an increasing sequence of closed sets. In particular, it is easy to show that complementation of sets maps Gm into itself for any limit ordinal m; moreover if m is an uncountable limit ordinal, Gm is closed under countable unions.
Note that for each Borel set B, there is some countable ordinal αB such that B can be obtained by iterating the operation over αB. However, as B varies over all Borel sets, αB will vary over all the countable ordinals, and thus the first ordinal at which all the Borel sets are obtained is ω1, the first uncountable ordinal.
Example
An important example, especially in the theory of probabilityProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, is the Borel algebra on the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. It is the algebra on which the Borel measure is defined. Given a real random variable defined on a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, its probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is by definition also a measure on the Borel algebra.
The Borel algebra on the reals is the smallest σ-algebra on R which contains all the intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
.
In the construction by transfinite induction, it can be shown that, in each step, the number of sets is, at most, the power of the continuum. So, the total number of Borel sets is less than or equal to
 .
.Standard Borel spaces and Kuratowski theorems
The following is one of a number of theorems of Kuratowski on Borel spaces:A Borel space is just another name for a set equipped with a distinguished σ-algebra; by extension elements of the distinguished σ-algebra are called Borel sets. Borel spaces form a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
in which the maps are Borel measurable mappings between Borel spaces, where

is Borel measurable means that f − 1(B) is Borel in X for any Borel subset B of Y.
Theorem. Let X be a Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
, that is, a topological space such that there is a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
d on X which defines the topology of X and which makes X a complete separable metric space. Then X as a Borel space is isomorphic to one of
(1) R, (2) Z or (3) a finite space.
Considered as Borel spaces, the real line R and the union of R with a countable set are isomorphic.
A standard Borel space is the Borel space associated to a Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
.
Note that any standard Borel space is defined (up to isomorphism) by its cardinality, and any uncountable standard Borel space has the cardinality of the continuum.
For subsets of Polish spaces, Borel sets can be characterized as those sets which are the ranges of continuous injective maps defined on Polish spaces. Note however, that the range of a continuous noninjective map may fail to be Borel. See analytic set
Analytic set
In descriptive set theory, a subset of a Polish space X is an analytic set if it is a continuous image of a Polish space. These sets were first defined by and his student .- Definition :There are several equivalent definitions of analytic set...
.
Every probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on a standard Borel space turns it into a standard probability space
Standard probability space
In probability theory, a standard probability space is a probability space satisfying certain assumptions introduced by Vladimir Rokhlin in 1940...
.
Non-Borel sets
An example of a subset of the reals which is non-Borel, due to LusinNikolai Luzin
Nikolai Nikolaevich Luzin, , was a Soviet/Russian mathematician known for his work in descriptive set theory and aspects of mathematical analysis with strong connections to point-set topology. He was the eponym of Luzitania, a loose group of young Moscow mathematicians of the first half of the...
, is described below. In contrast, an example of a non-measurable set
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
cannot be exhibited, though its existence can be proved.
Every irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
has a unique representation by a continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
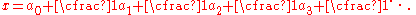
where
 is some integer
is some integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
and all the other numbers
 are positive integers. Let
are positive integers. Let 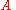 be the set of all irrational numbers that correspond to sequences
be the set of all irrational numbers that correspond to sequences  with the following property: there exists an infinite subsequence
with the following property: there exists an infinite subsequenceSubsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
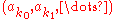 such that each element is a divisor
such that each element is a divisorDivisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of the next element. This set
 is not Borel. In fact, it is analytic
is not Borel. In fact, it is analyticAnalytic set
In descriptive set theory, a subset of a Polish space X is an analytic set if it is a continuous image of a Polish space. These sets were first defined by and his student .- Definition :There are several equivalent definitions of analytic set...
, and complete in the class of analytic sets. For more details see descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
and the book by Kechris
Alexander S. Kechris
Alexander Sotirios Kechris is a descriptive set theorist at Caltech. He has made major contributions to the theory of Borel equivalence relations....
, especially Exercise (27.2) on page 209, Definition (22.9) on page 169, and Exercise (3.4)(ii) on page 14.
Another non-Borel set is an inverse image
 of an infinite parity function
of an infinite parity function  . However, this is a proof of existence (via the choice axiom), not an explicit example.
. However, this is a proof of existence (via the choice axiom), not an explicit example.See also
- Baire setBaire setIn mathematics, more specifically in measure theory, the notion of a Baire set is important in the understanding of particular relations between measure theory and topology. In particular, an understanding of Baire sets aids in intuition when one deals with measures on non-metrizable topological...
- Cylindrical σ-algebra
- Polish spacePolish spaceIn the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
- Descriptive set theoryDescriptive set theoryIn mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...

