Inner model
Encyclopedia
In mathematical logic
, suppose T is a theory
in the language
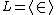
of set theory.
If M is a model of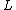
describing a set theory
and N is a class
of M such that
is a model
of T containing all ordinals
of M then we say that N is an inner model of T (in M). Ordinarily these models are transitive
subset
s or subclasses of the von Neumann universe
V, or sometimes of a generic extension of V
This term inner model is sometimes applied to models which are proper classes
; the term set model is used for models which are sets.
A model of set theory is called standard if the element relation of the model is the actual element relation restricted to the model. A model is called transitive when it is standard and the base class is a transitive class of sets. A model of set theory is often assumed to be transitive unless it is explicitly stated that it is non-standard. Inner models are transitive, transitive models are standard, and standard models are well-founded.
The assumption that there exists a standard model of ZFC (in a given universe) is stronger than the assumption that there exists a model. In fact, if there is a standard model, then there is a smallest standard model
called the minimal model
contained in all standard models. The minimal model contains no standard model (as it is minimal) but (assuming the consistency of ZFC) it contains
some model of ZFC by the Godel completeness theorem. This model is necessarily not well founded otherwise its Mostowski collapse
would be a standard model. (It is not well founded as a relation in the universe, though it
satisfies the axiom of foundation so is "internally" well founded. Being well founded is not an absolute property.)
In particular in the minimal model there is a model of ZFC but there is no standard model of ZFC.
a measurable cardinal
). When no theory is mentioned, it is usually assumed that the model under discussion is an inner model of ZFC. However, it is not uncommon to talk about inner models of subtheories of ZFC (like ZF or KP
) as well.
that any model of ZF has a least inner model of ZF (which is also an inner model of ZFC + GCH), called the constructible universe
, or L.
There is a branch of set theory called inner model theory
which studies ways of constructing least inner models of theories extending ZF. Inner model theory has led to the discovery of the exact consistency strength of many important set theoretical properties.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, suppose T is a theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
in the language
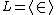
of set theory.
If M is a model of
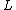describing a set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and N is a class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of M such that
is a model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of T containing all ordinals
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
of M then we say that N is an inner model of T (in M). Ordinarily these models are transitive
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s or subclasses of the von Neumann universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
V, or sometimes of a generic extension of V
This term inner model is sometimes applied to models which are proper classes
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
; the term set model is used for models which are sets.
A model of set theory is called standard if the element relation of the model is the actual element relation restricted to the model. A model is called transitive when it is standard and the base class is a transitive class of sets. A model of set theory is often assumed to be transitive unless it is explicitly stated that it is non-standard. Inner models are transitive, transitive models are standard, and standard models are well-founded.
The assumption that there exists a standard model of ZFC (in a given universe) is stronger than the assumption that there exists a model. In fact, if there is a standard model, then there is a smallest standard model
called the minimal model
Minimal model (set theory)
In set theory, a minimal model is a minimal standard model of ZFC.Minimal models were introduced by .The existence of a minimal model cannot be proved in ZFC, even assuming that ZFC is consistent, but follows from the existence of a standard model as follows...
contained in all standard models. The minimal model contains no standard model (as it is minimal) but (assuming the consistency of ZFC) it contains
some model of ZFC by the Godel completeness theorem. This model is necessarily not well founded otherwise its Mostowski collapse
Mostowski collapse
In mathematical logic, the Mostowski collapse lemma is a statement in set theory named for Andrzej Mostowski.-Statement:Suppose that R is a binary relation on a class X such that...
would be a standard model. (It is not well founded as a relation in the universe, though it
satisfies the axiom of foundation so is "internally" well founded. Being well founded is not an absolute property.)
In particular in the minimal model there is a model of ZFC but there is no standard model of ZFC.
Use
Usually when one talks about inner models of a theory, the theory one is discussing is ZFC or some extension of ZFC (like ZFC + a measurable cardinalMeasurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
). When no theory is mentioned, it is usually assumed that the model under discussion is an inner model of ZFC. However, it is not uncommon to talk about inner models of subtheories of ZFC (like ZF or KP
Kripke–Platek set theory
The Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...
) as well.
Related ideas
It was proved by Kurt GödelGodel
Godel or similar can mean:*Kurt Gödel , an Austrian logician, mathematician and philosopher*Gödel...
that any model of ZF has a least inner model of ZF (which is also an inner model of ZFC + GCH), called the constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
, or L.
There is a branch of set theory called inner model theory
Inner model theory
In set theory, inner model theory is the study of certain models of ZFC or some fragment or strengthening thereof. Ordinarily these models are transitive subsets or subclasses of the von Neumann universe V, or sometimes of a generic extension of V. Inner model theory studies the relationships of...
which studies ways of constructing least inner models of theories extending ZF. Inner model theory has led to the discovery of the exact consistency strength of many important set theoretical properties.
See also
- Countable transitive models and generic filters