Definable set
Encyclopedia
In mathematical logic
, a definable set is an n-ary relation
on the domain
of a structure
whose elements are precisely those elements satisfying some formula in the language of that structure. A set can be defined with or without parameters, which are elements of the domain that can be referenced in the formula defining the relation.
be a first-order language, 
an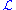 
-structure with domain 
, X a fixed subset of 
, and m a natural number. Then:
be the structure consisting of the natural number
s with the usual ordering. Then every natural is definable in
without parameters. The number 
is defined by the formula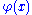 
stating that there exist no elements less than x:
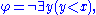
and a natural
is defined by the formula 
stating there exist exactly 
elements less than x:
In contrast, one cannot define any specific integer
without parameters in the structure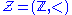
consisting of the integers with the usual ordering (see the section on automorphisms below).
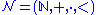be the first-order structure consisting of the natural numbers and their usual arithmetic operations and order relation. The sets definable in this structure are known as the arithmetical set
s, and are classified in the arithmetical hierarchy
. If the structure is considered in second-order logic
instead of first-order logic, the definable sets of natural numbers in the resulting structure are classified in the analytical hierarchy
. These hierarchies reveal many relationships between definability in this structure and computability theory
, and are also of interest in descriptive set theory
.
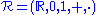be the structure consisting of the field
of real number
s. Although the usual ordering relation is not directly included in the structure, there is a formula that defines the set of nonnegative reals, since these are the only reals that possess square roots:
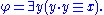
Thus any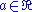
is nonnegative if and only if 
. In conjunction with a formula that defines the additive inverse of a real number in 
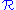, one can use 
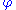to define the usual ordering in 
: for 
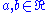, set 
if and only if 
is nonnegative. The enlarged structure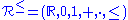 
s is called a definitional extension
of the original structure. It has the same expressive power as the original structure, in the sense that a set is definable over the enlarged structure from a set of parameters if and only if it is definable over the original structure from that same set of parameters.
The theory
of
has quantifier elimination
. Thus the definable sets are Boolean combinations of solutions to polynomial equalities and inequalities; these are called semi-algebraic sets. Generalizing this property of the real line leads to the study of o-minimality.
s.
This result can sometimes be used to classify the definable subsets of a given structure. For example, in the case of
above, any translation of 
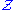is an automorphism preserving the empty set of parameters, and thus it is impossible to define any particular integer in this structure without parameters in 
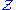. In fact, since any two integers are carried to each other by a translation and its inverse, the only sets of integers definable in 
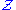without parameters are the empty set and 
itself.
s of a given structure.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a definable set is an n-ary relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
on the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of a structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
whose elements are precisely those elements satisfying some formula in the language of that structure. A set can be defined with or without parameters, which are elements of the domain that can be referenced in the formula defining the relation.
Definition
Let be a first-order language, an 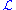-structure with domain , X a fixed subset of , and m a natural number. Then:- A set
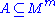is definable in 
with parameters from 
if and only if there exists a formula 
and elements 
such that for all 
,
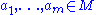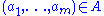if and only if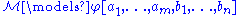 
The bracket notation here indicates the semantic evaluation of the free variables in the formula. - A set
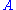is definable in 
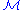without parameters if it is definable in 
with parameters from the empty set (that is, with no parameters in the defining formula). - A function is definable in
(with parameters) if its graph is definable (with those parameters) in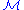 
. - An element a is definable in
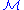(with parameters) if the singleton set {a} is definable in 
(with those parameters).
The natural numbers with only the order relation
Let be the structure consisting of the natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s with the usual ordering. Then every natural is definable in
without parameters. The number is defined by the formula 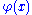stating that there exist no elements less than x: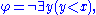and a natural
is defined by the formula stating there exist exactly elements less than x:In contrast, one cannot define any specific integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
without parameters in the structure
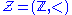consisting of the integers with the usual ordering (see the section on automorphisms below).The natural numbers with their arithmetical operations
Let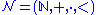 be the first-order structure consisting of the natural numbers and their usual arithmetic operations and order relation. The sets definable in this structure are known as the arithmetical setArithmetical set
In mathematical logic, an arithmetical set is a set of natural numbers that can be defined by a formula of first-order Peano arithmetic...
s, and are classified in the arithmetical hierarchy
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
. If the structure is considered in second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
instead of first-order logic, the definable sets of natural numbers in the resulting structure are classified in the analytical hierarchy
Analytical hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is a higher type analogue of the arithmetical hierarchy. It thus continues the classification of sets by the formulas that define them.-The analytical hierarchy of formulas:...
. These hierarchies reveal many relationships between definability in this structure and computability theory
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, and are also of interest in descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
.
The field of real numbers
Let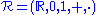 be the structure consisting of the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. Although the usual ordering relation is not directly included in the structure, there is a formula that defines the set of nonnegative reals, since these are the only reals that possess square roots:
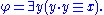
Thus any
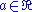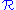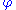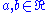is nonnegative if and only if . In conjunction with a formula that defines the additive inverse of a real number in , one can use to define the usual ordering in : for , set if and only if is nonnegative. The enlarged structure 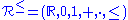s is called a definitional extensionExtension by definitions
In mathematical logic, more specifically in the proof theory of first-order theories, extensions by definitions formalize the introduction of new symbols by means of a definition. For example, it is common in naive set theory to introduce a symbol \emptyset for the set which has no member...
of the original structure. It has the same expressive power as the original structure, in the sense that a set is definable over the enlarged structure from a set of parameters if and only if it is definable over the original structure from that same set of parameters.
The theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
of
has quantifier eliminationQuantifier elimination
Quantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
. Thus the definable sets are Boolean combinations of solutions to polynomial equalities and inequalities; these are called semi-algebraic sets. Generalizing this property of the real line leads to the study of o-minimality.
Invariance under automorphisms
An important result about definable sets is that they are preserved under automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s.
- Let
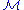be an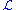 
-structure with domain 
, 
, and 
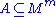definable in 
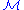with parameters from 
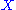. Let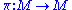 
be an automorphism of 
which is the identity on 
. Then for all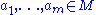 
,
-
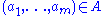if and only if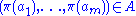 
This result can sometimes be used to classify the definable subsets of a given structure. For example, in the case of
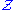above, any translation of is an automorphism preserving the empty set of parameters, and thus it is impossible to define any particular integer in this structure without parameters in 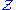. In fact, since any two integers are carried to each other by a translation and its inverse, the only sets of integers definable in 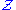without parameters are the empty set and itself.Additional results
The Tarski–Vaught test is used to characterize the elementary substructureElementary substructure
In model theory, a field within mathematical logic, two structures M and N of the same signature σ are called elementarily equivalent if they satisfy the same first-order σ-sentences....
s of a given structure.