Regular space
Encyclopedia
In topology
and related fields of mathematics
, a topological space
X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C
can be separated
by neighborhoods. This condition is known as Axiom T3. The term "T3 space" usually means "a regular Hausdorff space
". These conditions are examples of separation axiom
s.
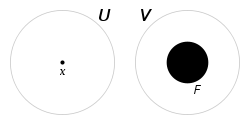A topological space
X is a regular space if, given any nonempty closed set
F and any point
x that does not belong to F, there exists a neighbourhood U of x and a neighbourhood V of F that are disjoint. Concisely put, it must be possible to separate x and F with disjoint neighborhoods.
A T3 space or regular Hausdorff space is a topological space that is both regular and a Hausdorff space
. (A Hausdorff space or T2 space is a topological space in which any two distinct points are separated by neighbourhoods.) It turns out that a space is T3 if and only if it is both regular and T0. (A T0 or Kolmogorov space
is a topological space in which any two distinct points are topologically distinguishable, i.e., for every pair of distinct points, at least one of them has an open neighborhood not containing the other.) Indeed, if a space is Hausdorff then it is T0, and each T0 regular space is Hausdorff: given two distinct points, at least one of them misses the closure of the other one, so (by regularity) there exist disjoint neighborhoods separating one point from (the closure of) the other.
Although the definitions presented here for "regular" and "T3" are not uncommon, there is significant variation in the literature: some authors switch the definitions of "regular" and "T3" as they are used here, or use both terms interchangeably. In this article, we will use the term "regular" freely, but we will usually say "regular Hausdorff", which is unambiguous, instead of the less precise "T3". For more on this issue, see History of the separation axioms
.
A locally regular space
is a topological space where every point has an open neighbourhood that is regular. Every regular space is locally regular, but the converse is not true. A classical example of a locally regular space that is not regular is the bug-eyed line.
Since a Hausdorff space is the same as a preregular T0 space
, a regular space that is also T0 must be Hausdorff (and thus T3).
In fact, a regular Hausdorff space satisfies the slightly stronger condition T2½.
(However, such a space need not be completely Hausdorff
.)
Thus, the definition of T3 may cite T0, T1
, or T2½ instead of T2 (Hausdorffness); all are equivalent in the context of regular spaces.
Speaking more theoretically, the conditions of regularity and T3-ness are related by Kolmogorov quotients.
A space is regular if and only if its Kolmogorov quotient is T3; and, as mentioned, a space is T3 if and only if it's both regular and T0.
Thus a regular space encountered in practice can usually be assumed to be T3, by replacing the space with its Kolmogorov quotient.
There are many results for topological spaces that hold for both regular and Hausdorff spaces.
Most of the time, these results hold for all preregular spaces; they were listed for regular and Hausdorff spaces separately because the idea of preregular spaces came later.
On the other hand, those results that are truly about regularity generally don't also apply to nonregular Hausdorff spaces.
There are many situations where another condition of topological spaces (such as normality
, paracompactness, or local compactness) will imply regularity if some weaker separation axiom, such as preregularity, is satisfied.
Such conditions often come in two versions: a regular version and a Hausdorff version.
Although Hausdorff spaces aren't generally regular, a Hausdorff space that is also (say) locally compact will be regular, because any Hausdorff space is preregular.
Thus from a certain point of view, regularity is not really the issue here, and we could impose a weaker condition instead to get the same result.
However, definitions are usually still phrased in terms of regularity, since this condition is more well known than any weaker one.
Most topological spaces studied in mathematical analysis
are regular; in fact, they are usually completely regular, which is a stronger condition.
Regular spaces should also be contrasted with normal space
s.
with respect to the small inductive dimension has a base
consisting of clopen set
s.
Every such space is regular.
As described above, any completely regular space is regular, and any T0 space that is not Hausdorff
(and hence not preregular) cannot be regular.
Most examples of regular and nonregular spaces studied in mathematics may be found in those two articles.
On the other hand, spaces that are regular but not completely regular, or preregular but not regular, are usually constructed only to provide counterexample
s to conjectures, showing the boundaries of possible theorem
s.
Of course, one can easily find regular spaces that are not T0, and thus not Hausdorff, such as an indiscrete space, but these examples provide more insight on the T0 axiom than on regularity. An example of a regular space that is not completely regular is the Tychonoff corkscrew.
Most interesting spaces in mathematics that are regular also satisfy some stronger condition.
Thus, regular spaces are usually studied to find properties and theorems, such as the ones below, that are actually applied to completely regular spaces, typically in analysis.
There exist Hausdorff spaces that are not regular. An example is the set R with the topology generated by sets of the form U - C, where U is an open set in the usual sense, and C is any countable subset of U.
Then, given any point x and neighbourhood G of x, there is a closed neighbourhood E of x that is a subset
of G.
In fancier terms, the closed neighbourhoods of x form a local base at x.
In fact, this property characterises regular spaces; if the closed neighbourhoods of each point in a topological space form a local base at that point, then the space must be regular.
Taking the interior
s of these closed neighbourhoods, we see that the regular open sets form a base
for the open sets of the regular space X.
This property is actually weaker than regularity; a topological space whose regular open sets form a base is semiregular
.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related fields of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C
can be separated
Separated sets
In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way....
by neighborhoods. This condition is known as Axiom T3. The term "T3 space" usually means "a regular Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
". These conditions are examples of separation axiom
Separation axiom
In topology and related fields of mathematics, there are several restrictions that one often makes on the kinds of topological spaces that one wishes to consider. Some of these restrictions are given by the separation axioms...
s.
Definitions
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X is a regular space if, given any nonempty closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
F and any point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
x that does not belong to F, there exists a neighbourhood U of x and a neighbourhood V of F that are disjoint. Concisely put, it must be possible to separate x and F with disjoint neighborhoods.
A T3 space or regular Hausdorff space is a topological space that is both regular and a Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. (A Hausdorff space or T2 space is a topological space in which any two distinct points are separated by neighbourhoods.) It turns out that a space is T3 if and only if it is both regular and T0. (A T0 or Kolmogorov space
Kolmogorov space
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
is a topological space in which any two distinct points are topologically distinguishable, i.e., for every pair of distinct points, at least one of them has an open neighborhood not containing the other.) Indeed, if a space is Hausdorff then it is T0, and each T0 regular space is Hausdorff: given two distinct points, at least one of them misses the closure of the other one, so (by regularity) there exist disjoint neighborhoods separating one point from (the closure of) the other.
Although the definitions presented here for "regular" and "T3" are not uncommon, there is significant variation in the literature: some authors switch the definitions of "regular" and "T3" as they are used here, or use both terms interchangeably. In this article, we will use the term "regular" freely, but we will usually say "regular Hausdorff", which is unambiguous, instead of the less precise "T3". For more on this issue, see History of the separation axioms
History of the separation axioms
In general topology, the separation axioms have had a convoluted history, with many competing meanings for the same term, and many competing terms for the same concept.- Origins :...
.
A locally regular space
Locally regular space
In mathematics, particularly topology, a topological space X is locally regular if intuitively it looks locally like a regular space. More precisely, a locally regular space satisfies the property that each point of the space belongs to an open subset of the space that is regular under the subspace...
is a topological space where every point has an open neighbourhood that is regular. Every regular space is locally regular, but the converse is not true. A classical example of a locally regular space that is not regular is the bug-eyed line.
Relationships to other separation axioms
A regular space is necessarily also preregular, i.e., any two topologically distinguishable points can be separated by neighbourhoods.Since a Hausdorff space is the same as a preregular T0 space
Kolmogorov space
In topology and related branches of mathematics, a topological space X is a T0 space or Kolmogorov space if for every pair of distinct points of X, at least one of them has an open neighborhood not containing the other. This condition, called the T0 condition, is one of the separation axioms...
, a regular space that is also T0 must be Hausdorff (and thus T3).
In fact, a regular Hausdorff space satisfies the slightly stronger condition T2½.
(However, such a space need not be completely Hausdorff
Completely Hausdorff space
In topology, an Urysohn space, or T2½ space, is a topological space in which any two distinct points can be separated by closed neighborhoods. A completely Hausdorff space, or functionally Hausdorff space, is a topological space in which any two distinct points can be separated by a continuous...
.)
Thus, the definition of T3 may cite T0, T1
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
, or T2½ instead of T2 (Hausdorffness); all are equivalent in the context of regular spaces.
Speaking more theoretically, the conditions of regularity and T3-ness are related by Kolmogorov quotients.
A space is regular if and only if its Kolmogorov quotient is T3; and, as mentioned, a space is T3 if and only if it's both regular and T0.
Thus a regular space encountered in practice can usually be assumed to be T3, by replacing the space with its Kolmogorov quotient.
There are many results for topological spaces that hold for both regular and Hausdorff spaces.
Most of the time, these results hold for all preregular spaces; they were listed for regular and Hausdorff spaces separately because the idea of preregular spaces came later.
On the other hand, those results that are truly about regularity generally don't also apply to nonregular Hausdorff spaces.
There are many situations where another condition of topological spaces (such as normality
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
, paracompactness, or local compactness) will imply regularity if some weaker separation axiom, such as preregularity, is satisfied.
Such conditions often come in two versions: a regular version and a Hausdorff version.
Although Hausdorff spaces aren't generally regular, a Hausdorff space that is also (say) locally compact will be regular, because any Hausdorff space is preregular.
Thus from a certain point of view, regularity is not really the issue here, and we could impose a weaker condition instead to get the same result.
However, definitions are usually still phrased in terms of regularity, since this condition is more well known than any weaker one.
Most topological spaces studied in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
are regular; in fact, they are usually completely regular, which is a stronger condition.
Regular spaces should also be contrasted with normal space
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
s.
Examples and nonexamples
A zero-dimensional spaceZero-dimensional space
In mathematics, a zero-dimensional topological space is a topological space that has dimension zero with respect to one of several inequivalent notions of assigning a dimension to a given topological space...
with respect to the small inductive dimension has a base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
consisting of clopen set
Clopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
s.
Every such space is regular.
As described above, any completely regular space is regular, and any T0 space that is not Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
(and hence not preregular) cannot be regular.
Most examples of regular and nonregular spaces studied in mathematics may be found in those two articles.
On the other hand, spaces that are regular but not completely regular, or preregular but not regular, are usually constructed only to provide counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
s to conjectures, showing the boundaries of possible theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s.
Of course, one can easily find regular spaces that are not T0, and thus not Hausdorff, such as an indiscrete space, but these examples provide more insight on the T0 axiom than on regularity. An example of a regular space that is not completely regular is the Tychonoff corkscrew.
Most interesting spaces in mathematics that are regular also satisfy some stronger condition.
Thus, regular spaces are usually studied to find properties and theorems, such as the ones below, that are actually applied to completely regular spaces, typically in analysis.
There exist Hausdorff spaces that are not regular. An example is the set R with the topology generated by sets of the form U - C, where U is an open set in the usual sense, and C is any countable subset of U.
Elementary properties
Suppose that X is a regular space.Then, given any point x and neighbourhood G of x, there is a closed neighbourhood E of x that is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of G.
In fancier terms, the closed neighbourhoods of x form a local base at x.
In fact, this property characterises regular spaces; if the closed neighbourhoods of each point in a topological space form a local base at that point, then the space must be regular.
Taking the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
s of these closed neighbourhoods, we see that the regular open sets form a base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for the open sets of the regular space X.
This property is actually weaker than regularity; a topological space whose regular open sets form a base is semiregular
Semiregular space
A semiregular space is a topological space whose regular open sets form a base.Every regular space is semiregular, and every topological space may be embedded into a semiregular space....
.