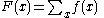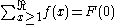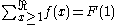Indefinite sum
Encyclopedia
In mathematics
the indefinite sum operator (also known as the antidifference operator), denoted by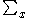
or 
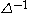, is the linear operator, inverse of the forward difference operator 
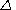. It relates to the forward difference operator as the indefinite integral relates to the derivative
. Thus
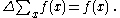
More explicitly, if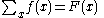
, then
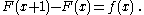
If F(x) is a solution of this functional equation for a given f(x), then so is F(x)+C for any constant C. Therefore each indefinite sum actually represents a family of functions, differing by an additive constant.
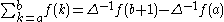
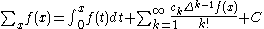
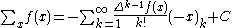
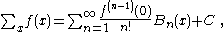
provided that the right-hand side of the equation converges.
then
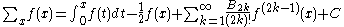
or
In this case, where
then Ramanjuan's sum is defined as
or
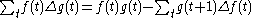
Definite summation by parts: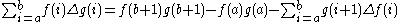
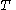is a period of function 
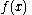then
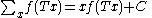
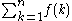
In this case a closed form expression F(k) for the sum is a solution of
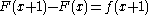which is called the telescoping equation. It is inverse to backward difference 
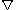operator.
It is related to the forward antidifference operator using the fundamental theorem of discrete calculus described earlier.
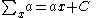
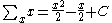
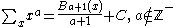
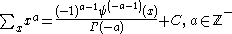
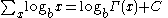
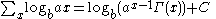
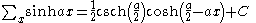
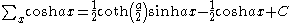
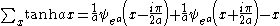
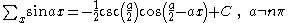
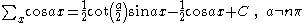
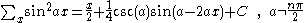
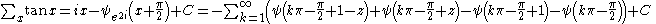
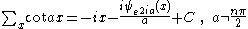
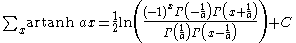
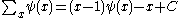
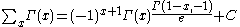
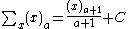
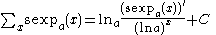
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the indefinite sum operator (also known as the antidifference operator), denoted by
or , is the linear operator, inverse of the forward difference operator . It relates to the forward difference operator as the indefinite integral relates to the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. Thus
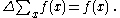
More explicitly, if
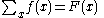, then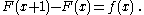If F(x) is a solution of this functional equation for a given f(x), then so is F(x)+C for any constant C. Therefore each indefinite sum actually represents a family of functions, differing by an additive constant.
Fundamental theorem of discrete calculus
Indefinite sums can be used to calculate definite sums with the formula: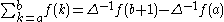Laplace summation formula
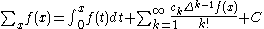
- where
are the Bernoulli numbers of the second kind.
Newton's formula
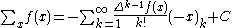
- where
is the falling factorial.
Faulhaber's formula
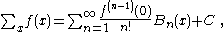
provided that the right-hand side of the equation converges.
Mueller's formula
Ifthen
Ramanujan's formula
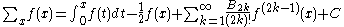
Connection to the Ramanujan summation
Often the constant C in indefinite sum is fixed from the following equation:
or
In this case, where
then Ramanjuan's sum is defined as
or
Summation by parts
Indefinite summation by parts: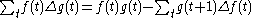Definite summation by parts:
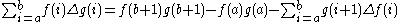
Period rule
If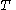 is a period of functio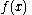n then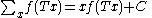Alternative usage
Some authors use the phrase "indefinite sum" to describe a sum in which the numerical value of the upper limit is not given. e.g.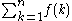In this case a closed form expression F(k) for the sum is a solution of
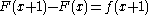which is called the telescoping equation. It is inverse to backward difference operator.It is related to the forward antidifference operator using the fundamental theorem of discrete calculus described earlier.
List of indefinite sums
This is a list of indefinite sums of various functions. Not every function has an indefinite sum that can be expressed in terms of elementary functions.Antidifferences of rational functions
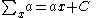
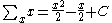
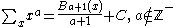
- where
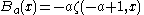, the generalized to real order Bernoulli polynomialsBernoulli polynomialsIn mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
.
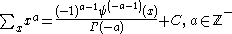
- where
is the polygamma function.
- where
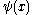is the digamma function.
Antidifferences of logarithmic functions
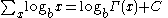
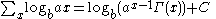
Antidifferences of hyperbolic functions
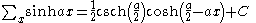
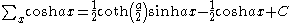
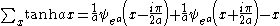
- where
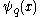is the q-digammaQ-analogRoughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
function.
Antidifferences of trigonometric functions
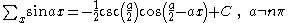
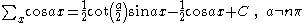
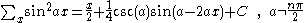
- where
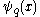is the q-digammaQ-analogRoughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
function.
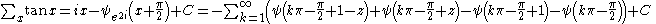
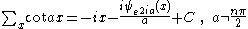
Antidifferences of inverse hyperbolic functions
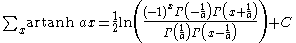
Antidifferences of inverse trigonometric functions
Antidifferences of special functions
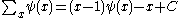
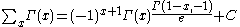
- where
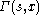is the incomplete gamma functionIncomplete gamma functionIn mathematics, the gamma function is defined by a definite integral. The incomplete gamma function is defined as an integral function of the same integrand. There are two varieties of the incomplete gamma function: the upper incomplete gamma function is for the case that the lower limit of...
.
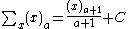
- where
is the falling factorial.
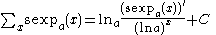
See also
- Indefinite product
- Time scale calculusTime scale calculusIn mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid discrete–continuous dynamical systems...
- List of derivatives and integrals in alternative calculi
Further reading
- "Difference Equations: An Introduction with Applications", Walter G. Kelley, Allan C. Peterson, Academic Press, 2001, ISBN 012403330X
- Markus Müller. How to Add a Non-Integer Number of Terms, and How to Produce Unusual Infinite Summations
- Markus Mueller, Dierk Schleicher. Fractional Sums and Euler-like Identities
- S. P. Polyakov. Indefinite summation of rational functions with additional minimization of the summable part. Programmirovanie, 2008, Vol. 34, No. 2.