
Decayotton
Encyclopedia
| Regular decayotton (9-simplex) |
|
|---|---|
Orthogonal projection inside Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... |
|
| Type | Regular 9-polytope 9-polytope In nine-dimensional geometry, a polyyotton is a polytope contained by 8-polytope facets. Each 7-polytope ridge being shared by exactly two 8-polytope facets.... |
| Family | simplex Simplex In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,... |
| Schläfli symbol | {3,3,3,3,3,3,3,3} |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|
| 8-faces | 10 8-simplex |
| 7-faces | 45 7-simplex |
| 6-faces | 120 6-simplex |
| 5-faces | 210 5-simplex |
| 4-faces | 252 5-cell |
| Cells | 210 tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
| Faces | 120 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... |
| Edges | 45 |
| Vertices | 10 |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
8-simplex |
| Petrie polygon Petrie polygon In geometry, a Petrie polygon for a regular polytope of n dimensions is a skew polygon such that every consecutive sides belong to one of the facets... |
decagon Decagon In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°... |
| Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
A9 [3,3,3,3,3,3,3,3] |
| Dual | Self-dual |
| Properties | convex Convex polytope A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn... |
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a 9-simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
is a self-dual regular
Regular polytope
In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
9-polytope
9-polytope
In nine-dimensional geometry, a polyyotton is a polytope contained by 8-polytope facets. Each 7-polytope ridge being shared by exactly two 8-polytope facets....
. It has 10 vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
, 45 edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
s, 120 triangle faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
, 210 tetrahedral cells, 252 5-cell 4-faces, 210 5-simplex 5-faces, 120 6-simplex 6-faces, 45 7-simplex 7-faces, and 10 8-simplex 8-faces. Its dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
is cos−1(1/9), or approximately 83.62°.
It can also be called a decayotton, or deca-9-tope, as a 10-facetted polytope in 9-dimensions.. The name decayotton is derived from deca for ten facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
in Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
and -yott
Yotta
Yotta is the largest unit prefix in the International System of Units denoting a factor of 1024 or . It has the unit symbol Y.The prefix name is derived from the Greek , meaning eight, because it is equal to 10008...
(variation of oct for eight), having 8-dimensional facets, and -on.
Coordinates
The Cartesian coordinates of the vertices of an origin-centered regular decayotton having edge length 2 are: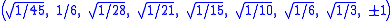
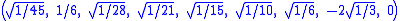
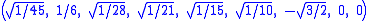

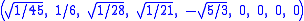
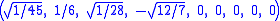
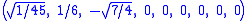
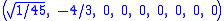
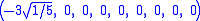
More simply, the vertices of the 9-simplex can be positioned in 10-space as permutations of (0,0,0,0,0,0,0,0,1). This construction is based on facets of the 10-orthoplex.

