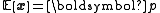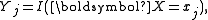Categorical distribution
Encyclopedia
In probability theory
and statistics
, a categorical distribution (occasionally termed the "discrete distribution", which properly refers to a general class of distributions) is a probability distribution
that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified. There is not necessarily an underlying ordering of these outcomes, but numerical labels are attached for convenience in describing the distribution, often in the range 1 to K. Note that the K-dimensional categorical distribution is the most general distribution over a K-way event; any other discrete distribution over a size-K sample space is a special case. The parameters specifying the probabilities of each possible outcome are constrained only by the fact that each must be in the range 0 to 1, and all must sum to 1.
Note that, in some fields, such as natural language processing
, the categorical and multinomial distributions are conflated, and it is common to speak of a "multinomial distribution" when a categorical distribution is actually meant. This stems from the fact that it is sometimes convenient to express the outcome of a categorical distribution as a "1-of-K" vector (a vector with one element containing a 1 and all other elements containing a 0) rather than as an integer in the range 1 to K; in this form, a categorical distribution is equivalent to a multinomial distribution for a single observation (see below).
On one formulation of the distribution, the sample space is taken to be a finite sequence of integers. The items might be encoded as {0, 1, ..., n-1} or {1, 2, ..., n} for example: the latter is used here, although the former is the used for the Bernoulli distribution. In this case, the probability mass function
f is:

where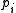 represents the probability of seeing element i and
represents the probability of seeing element i and 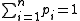 .
.
In another formulation, the categorical distribution is a special case of the multinomial distribution in which the parameter n of the multinomial distribution is fixed at 1. In this formulation, the sample space can be considered to be the set of 1-of-N encoded (also known as 1-of-K encoded) random vectors x of dimension n having the property that exactly one element has the value 1 and the others have the value 0. The probability mass function
f in this formulation is:
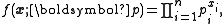
where represents the probability of seeing element i and
represents the probability of seeing element i and 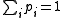 .
.
This is the formulation adopted by Bishop However, Bishop does not explicitly use the term categorical distribution.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a categorical distribution (occasionally termed the "discrete distribution", which properly refers to a general class of distributions) is a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
that describes the result of a random event that can take on one of K possible outcomes, with the probability of each outcome separately specified. There is not necessarily an underlying ordering of these outcomes, but numerical labels are attached for convenience in describing the distribution, often in the range 1 to K. Note that the K-dimensional categorical distribution is the most general distribution over a K-way event; any other discrete distribution over a size-K sample space is a special case. The parameters specifying the probabilities of each possible outcome are constrained only by the fact that each must be in the range 0 to 1, and all must sum to 1.
Note that, in some fields, such as natural language processing
Natural language processing
Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....
, the categorical and multinomial distributions are conflated, and it is common to speak of a "multinomial distribution" when a categorical distribution is actually meant. This stems from the fact that it is sometimes convenient to express the outcome of a categorical distribution as a "1-of-K" vector (a vector with one element containing a 1 and all other elements containing a 0) rather than as an integer in the range 1 to K; in this form, a categorical distribution is equivalent to a multinomial distribution for a single observation (see below).
Introduction
A categorical distribution is a discrete probability distribution whose sample space is the set of n individually identified items. It is the generalization of the Bernoulli distribution for a categorical random variable.On one formulation of the distribution, the sample space is taken to be a finite sequence of integers. The items might be encoded as {0, 1, ..., n-1} or {1, 2, ..., n} for example: the latter is used here, although the former is the used for the Bernoulli distribution. In this case, the probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
f is:

where
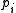 represents the probability of seeing element i and
represents the probability of seeing element i and 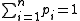 .
.In another formulation, the categorical distribution is a special case of the multinomial distribution in which the parameter n of the multinomial distribution is fixed at 1. In this formulation, the sample space can be considered to be the set of 1-of-N encoded (also known as 1-of-K encoded) random vectors x of dimension n having the property that exactly one element has the value 1 and the others have the value 0. The probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
f in this formulation is:
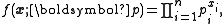
where
 represents the probability of seeing element i and
represents the probability of seeing element i and 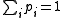 .
.This is the formulation adopted by Bishop However, Bishop does not explicitly use the term categorical distribution.
Properties

- The distribution is completely given by the probabilities associated with each number k:
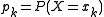 , k = 1,...,n, where
, k = 1,...,n, where 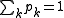 . The possible probabilities are exactly the standard
. The possible probabilities are exactly the standard 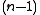 -dimensional simplex; for n = 2 this reduces to the possible probabilities of the Bernoulli distribution being the 1-simplex,
-dimensional simplex; for n = 2 this reduces to the possible probabilities of the Bernoulli distribution being the 1-simplex, 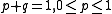 .
.
- The distribution is a special case of a "multivariate Bernoulli distribution" in which exactly one of the n 0-1 variables takes the value one.
- Let
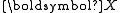 be the realisation from a categorical distribution. Define the random vector Y as composed of the elements:
be the realisation from a categorical distribution. Define the random vector Y as composed of the elements:
-
- where I is the indicator function. Then Y has a distribution which is a special case of the multinomial distribution with parameter
 . The sum of
. The sum of  independent and identically distributed such random variables Y constructed from a categorical distribution with parameter
independent and identically distributed such random variables Y constructed from a categorical distribution with parameter 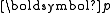 is multinomially distributed with parameters
is multinomially distributed with parameters  and
and 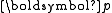
- The sufficient statistic from n independent observations is the set of counts (or, equivalently, proportion) of observations in each category, where the total number of trials (=n) is fixed.
- The conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
is the Dirichlet distribution.
- The indicator function of an observation,
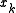 , is Bernoulli distributed with parameter
, is Bernoulli distributed with parameter 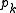 .
.