
Polynomial and rational function modeling
Encyclopedia
In statistical modeling (especially process modeling
), polynomial functions and rational functions are sometimes used as an empirical technique for curve fitting
.
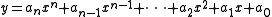
where n is a non-negative integer
that defines the degree of the polynomial. A polynomial with a degree of 0 is simply a constant function
; with a degree of 1 is a line
; with a degree of 2 is a quadratic
; with a degree of 3 is a cubic
, and so on.
Historically, polynomial models are among the most frequently used empirical models for curve fitting
.
When modeling via polynomial functions is inadequate due to any of the limitations above, the use of rational functions for modeling may give a better fit.
is simply the ratio of two polynomial functions.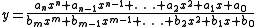
with n denoting a non-negative integer that defines the degree of the numerator and m is a non-negative integer that defines the degree of the denominator. For fitting rational function models, the constant term in the denominator is usually set to 1. Rational functions are typically identified by the degrees of the numerator and denominator. For example, a quadratic for the numerator and a cubic for the denominator is identified as a quadratic/cubic rational function. A rational function model is a generalization of the polynomial model: rational function models contain polynomial models as a subset (i.e., the case when the denominator is a constant).
One common difficulty in fitting nonlinear models is finding adequate starting values. A major advantage of rational function models is the ability to compute starting values using a linear least squares
fit. To do this, p points are chosen from the data set, with p denoting the number of parameters in the rational model. For example, given the linear/quadratic model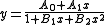
one would need to select four representative points, and perform a linear fit on the model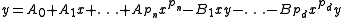
Here, pn and pd are the degrees of the numerator and denominator, respectively, and the x and y contain the subset of points, not the full data set. The estimated coefficients from this linear fit are used as the starting values for fitting the nonlinear model to the full data set.
Note: This type of fit, with the response variable appearing on both sides of the function, should only be used to obtain starting values for the nonlinear fit. The statistical properties of fits like this are not well understood.
The subset of points should be selected over the range of the data. It is not critical which points are selected, although obvious outliers should be avoided.
Process modeling
The term process model is used in various contexts. For example, in business process modeling the enterprise process model is often referred to as the business process model. Process models are core concepts in the discipline of process engineering....
), polynomial functions and rational functions are sometimes used as an empirical technique for curve fitting
Curve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
.
Polynomial function models
A polynomial function is one that has the form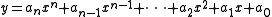
where n is a non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
that defines the degree of the polynomial. A polynomial with a degree of 0 is simply a constant function
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
; with a degree of 1 is a line
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
; with a degree of 2 is a quadratic
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
; with a degree of 3 is a cubic
Cubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
, and so on.
Historically, polynomial models are among the most frequently used empirical models for curve fitting
Curve fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
.
Advantages
These models are popular for the following reasons.- Polynomial models have a simple form.
- Polynomial models have well known and understood properties.
- Polynomial models have moderate flexibility of shapes.
- Polynomial models are a closed family. Changes of locationTranslation (geometry)In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
and scaleScaling (geometry)In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
in the raw data result in a polynomial model being mapped to a polynomial model. That is, polynomial models are not dependent on the underlying metricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
. - Polynomial models are computationally easy to use.
Disadvantages
However, polynomial models also have the following limitations.- Polynomial models have poor interpolatoryInterpolationIn the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
properties. High-degree polynomials are notorious for oscillations between exact-fit valuesRunge's phenomenonIn the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree...
. - Polynomial models have poor extrapolatoryExtrapolationIn mathematics, extrapolation is the process of constructing new data points. It is similar to the process of interpolation, which constructs new points between known points, but the results of extrapolations are often less meaningful, and are subject to greater uncertainty. It may also mean...
properties. Polynomials may provide good fits within the range of data, but they will frequently deteriorate rapidly outside the range of the data. - Polynomial models have poor asymptoticAsymptoteIn analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
properties. By their nature, polynomials have a finite response for finite x values and have an infinite response if and only if the x value is infinite. Thus polynomials may not model asymptotic phenomena very well. - While no procedure is immune to the biasBias of an estimatorIn statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
-varianceVarianceIn probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
tradeoff, polynomial models exhibit a particularly poor tradeoff between shape and degree. In order to model data with a complicated structure, the degree of the model must be high, indicating that the associated number of parameterStatistical parameterA statistical parameter is a parameter that indexes a family of probability distributions. It can be regarded as a numerical characteristic of a population or a model....
s to be estimatedEstimation theoryEstimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
will also be high. This can result in highly unstable models.
When modeling via polynomial functions is inadequate due to any of the limitations above, the use of rational functions for modeling may give a better fit.
Rational function models
A rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
is simply the ratio of two polynomial functions.
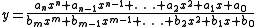
with n denoting a non-negative integer that defines the degree of the numerator and m is a non-negative integer that defines the degree of the denominator. For fitting rational function models, the constant term in the denominator is usually set to 1. Rational functions are typically identified by the degrees of the numerator and denominator. For example, a quadratic for the numerator and a cubic for the denominator is identified as a quadratic/cubic rational function. A rational function model is a generalization of the polynomial model: rational function models contain polynomial models as a subset (i.e., the case when the denominator is a constant).
Advantages
Rational function models have the following advantages:- Rational function models have a moderately simple form.
- Rational function models are a closed family. As with polynomial models, this means that rational function models are not dependent on the underlying metric.
- Rational function models can take on an extremely wide range of shapes, accommodating a much wider range of shapes than does the polynomial family.
- Rational function models have better interpolatory properties than polynomial models. Rational functions are typically smoother and less oscillatory than polynomial models.
- Rational functions have excellent extrapolatory powers. Rational functions can typically be tailored to model the function not only within the domain of the data, but also so as to be in agreement with theoretical/asymptotic behavior outside the domain of interest.
- Rational function models have excellent asymptotic properties. Rational functions can be either finite or infinite for finite values, or finite or infinite for infinite x values. Thus, rational functions can easily be incorporated into a rational function model.
- Rational function models can often be used to model complicated structure with a fairly low degree in both the numerator and denominator. This in turn means that fewer coefficients will be required compared to the polynomial model.
- Rational function models are moderately easy to handle computationally. Although they are nonlinear modelsNonlinear regressionIn statistics, nonlinear regression is a form of regression analysis in which observational data are modeled by a function which is a nonlinear combination of the model parameters and depends on one or more independent variables...
, rational function models are particularly easy nonlinear models to fit.
Disadvantages
Rational function models have the following disadvantages:- The properties of the rational function family are not as well known to engineers and scientists as are those of the polynomial family. The literature on the rational function family is also more limited. Because the properties of the family are often not well understood, it can be difficult to answer the following modeling question: Given that data has a certain shape, what values should be chosen for the degree of the numerator and the degree on the denominator?
- Unconstrained rational function fitting can, at times, result in undesired vertical asymptoteAsymptoteIn analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s due to roots in the denominator polynomial. The range of x values affected by the function "blowing up" may be quite narrow, but such asymptotes, when they occur, are a nuisance for local interpolation in the neighborhood of the asymptote point. These asymptotes are easy to detect by a simple plot of the fitted function over the range of the data. These nuisance asymptotes occur occasionally and unpredictably, but practitioners argue that the gain in flexibility of shapes is well worth the chance that they may occur, and that such asymptotes should not discourage choosing rational function models for empirical modeling.
One common difficulty in fitting nonlinear models is finding adequate starting values. A major advantage of rational function models is the ability to compute starting values using a linear least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
fit. To do this, p points are chosen from the data set, with p denoting the number of parameters in the rational model. For example, given the linear/quadratic model
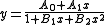
one would need to select four representative points, and perform a linear fit on the model
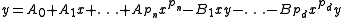
Here, pn and pd are the degrees of the numerator and denominator, respectively, and the x and y contain the subset of points, not the full data set. The estimated coefficients from this linear fit are used as the starting values for fitting the nonlinear model to the full data set.
Note: This type of fit, with the response variable appearing on both sides of the function, should only be used to obtain starting values for the nonlinear fit. The statistical properties of fits like this are not well understood.
The subset of points should be selected over the range of the data. It is not critical which points are selected, although obvious outliers should be avoided.

