Regular polyhedron
Encyclopedia
A regular polyhedron is a polyhedron
whose faces are congruent
regular polygons which are assembled in the same way around each vertex
. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive
and face-transitive - i.e. it is transitive on its flags. This last alone is a sufficient definition.
A regular polyhedron is identified by its Schläfli symbol of the form {n, m}, where n is the number of sides of each face and m the number of faces meeting at each vertex. There are 5 finite regular polyhedra, which are called the Platonic solid
s, the self-dual tetrahedron
{3,3}, dual-pair cube
/octahedron
{4,3}, and dual pair dodecahedron/icosahedron
{5,3}.
regular polyhedra, known as the Platonic solid
s:
, the Kepler-Poinsot polyhedra:
The property of having a similar arrangement of faces around each vertex can be replaced by any of the following equivalent conditions in the definition:
Concentric spheres
A regular polyhedron has all of three related spheres (other polyhedra lack at least one kind) which share its centre:
Symmetry
The regular polyhedra are the most symmetrical
of all the polyhedra. They lie in just three symmetry group
s, which are named after them:
Any shapes with icosahedral or octahedral symmetry will also contain tetrahedral symmetry.
Euler characteristic
The five Platonic solids have an Euler characteristic
of 2. Some of the regular stars have a different value.
to the other (i.e. the vertices of one polyhedron correspond to the faces of the other, and vice versa):
The Schläfli symbol of the dual is just the original written backwards, for example the dual of {5, 3} is {3, 5}.
For further information please see the individual articles or the general polyhedron
article.
and may be as much as 4,000 years old. These stones show not only the form of each of the five Platonic solids, but also the relations of duality amongst them (that is, that the centres of the faces of the cube gives the vertices of an octahedron, and so on). Examples of these stones are on display in the John Evans room of the Ashmolean Museum
at Oxford University. Why these objects were made, or how their creators gained the inspiration for them, is a mystery.
It is also possible that the Etruscans
preceded the Greeks in their awareness of at least some of the regular polyhedra, as evidenced by the discovery near Padua
(in Northern Italy
) in the late 19th century of a dodecahedron made of soapstone
, and dating back more than 2,500 years (Lindemann, 1987). Pyritohedric crystals are found in northern Italy.
, (an Athenian
), was the first to give a mathematical description of all five (Van der Waerden, 1954), (Euclid, book XIII). H.S.M. Coxeter (Coxeter, 1948, Section 1.9) credits Plato
(400 BC) with having made models of them, and mentions that one of the earlier Pythagoreans, Timaeus of Locri
, used all five in a correspondence between the polyhedra and the nature of the universe as it was then perceived - this correspondence is recorded in Plato's dialogue Timaeus
. Euclid's reference to Plato led to their common description as the Platonic solids.
One might characterise the Greek definition as follows:
This definition rules out, for example, the square pyramid
(since although all the faces are regular, the square base is not congruent to the triangular sides), or the shape formed by joining two tetrahedra together (since although all faces of that triangular bipyramid would be equilateral triangles, that is, congruent and regular, some vertices have 3 triangles and others have 4).
This concept of a regular polyhedron would remain unchallenged for almost 2000 years.
(star pentagon) were also known to the ancient Greeks - the pentagram
was used by the Pythagoreans as their secret sign, but they did not use them to construct polyhedra. It was not until the early 17th century that Johannes Kepler
realised that pentagrams could be used as the faces of regular star polyhedra
. Some of these star polyhedra may have been discovered by others before Kepler's time, but Kepler was the first to recognise that they could be considered "regular" if one removed the restriction that regular polyhedra be convex. Two hundred years later Louis Poinsot
also allowed star vertex figure
s (circuits around each corner), enabling him to discover two new regular star polyhedra along with rediscovering Kepler's. These four are the only regular star polyhedra, and have come to be known as the Kepler-Poinsot polyhedra. It was not until the mid-19th century, several decades after Poinsot published, that Cayley gave them their modern English names: (Kepler's) small stellated dodecahedron and great stellated dodecahedron, and (Poinsot's) great icosahedron and great dodecahedron.
The Kepler-Poinsot polyhedra may be constructed from the Platonic solids by a process called stellation
. The reciprocal process to stellation is called facetting
(or faceting). Every stellation of one polyhedron is dual
, or reciprocal, to some facetting of the dual polyhedron. The regular star polyhedra can also be obtained by facetting the Platonic solids. This was first done by Bertrand around the same time that Cayley named them.
By the end of the 19th century there were therefore nine regular polyhedra - five convex and four star.
The tetrahedron, cube, and octahedron all occur as crystal
s. These by no means exhaust the numbers of possible forms of crystals (Smith, 1982, p212), of which there are 48. Neither the regular icosahedron nor the regular dodecahedron are amongst them, although one of the forms, called the pyritohedron
, has twelve pentagonal faces arranged in the same pattern as the faces of the regular dodecahedron. The faces of the pyritohedron are, however, not regular, so the pyritohedron is also not regular.
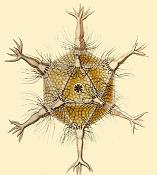Polyhedra appear in biology as well. In the early 20th century, Ernst Haeckel
described a number of species of Radiolaria, some of whose skeletons are shaped like various regular polyhedra. (Haeckel, 1904) Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra; the shapes of these creatures are indicated by their names. The outer protein shells of many virus
es form regular polyhedra. For example, HIV
is enclosed in a regular icosahedron.
A more recent discovery is of a series of new types of carbon
molecule, known as the fullerene
s (see (Curl, 1991) for an exposition of this discovery). Although C60, the most easily produced fullerene, looks more or less spherical, some of the larger varieties (such as C240, C480 and C960) are hypothesised to take on the form of slightly rounded icosahedra, a few nanometres across.
In ancient times the Pythagoreans
believed that there was a harmony between the regular polyhedra and the orbits of the planet
s. In the 17th century, Johannes Kepler
studied data on planetary motion compiled by Tycho Brahe
and for a decade tried to establish the Pythagorean ideal by finding a match between the sizes of the polyhedra and the sizes of the planets' orbits. His search failed in its original objective, but out of this research came Kepler's discoveries of the Kepler solids as regular polytopes, the realisation that the orbits of planets are not circles, and the laws of planetary motion
for which he is now famous. In Kepler's time only five planets (excluding the earth) were known, nicely matching the number of Platonic solids. Kepler's work, and the discovery since that time of Uranus
and Neptune
, have invalidated the Pythagorean idea.
Around the same time as the Pythagoreans, Plato described a theory of matter in which the five elements (earth, air, fire, water and spirit) each comprised tiny copies of one of the five regular solids. Matter was built up from a mixture of these polyhedra, with each substance having different proportions in the mix. Two thousand years later Dalton's atomic theory would show this idea to be along the right lines, though not related directly to the regular solids.
. Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure
, with m regular l-gons around a vertex. The n defines n-gonal holes. Their vertex figures are regular skew polygons, vertices zig-zagging between two planes.
Finite regular skew polyhedra exist in 4-space. These finite regular skew polyhedra in 4-space can be seen as a subset of the faces of uniform polychoron
s. Two dual solutions are related to the 5-cell, two dual solutions are related to the 24-cell, and an infinite set of self-dual duoprism
s generate regular skew polyhedra as {4, 4 | n}. In the infinite limit these approach a duocylinder and look like a torus
in their stereographic projection
s into 3-space.
, elliptic and complex
spaces, discovered over the preceding century, led to the discovery of more new polyhedra such as complex polyhedra
which could only take regular geometric form in those spaces.
s in any number of dimensions. The second half of the century saw the development of abstract algebraic ideas such as Polyhedral combinatorics
, culminating in the idea of an abstract polytope
as a partially ordered set
(poset) of elements. The elements of an abstract polyhedron are its body (the maximal element), its faces, edges, vertices and the null polytope or empty set. These abstract elements can be mapped into ordinary space or realised as geometrical figures. Some abstract polyhedra have well-formed or faithful realisations, others do not. A flag is a connected set of elements of each dimension - for a polyhedron that is the body, a face, an edge of the face, a vertex of the edge, and the null polytope. An abstract polytope is said to be regular if its combinatorial symmetries are transitive on its flags - that is to say, that any flag can be mapped onto any other under a symmetry of the polyhedron. Abstract regular polytopes remain an active area of research.
Five such regular abstract polyhedra, which can not be realised faithfully, were identified by H. S. M. Coxeter in his book Regular Polytopes (1977) and again by J. M. Wills in his paper "The combinatorially regular polyhedra of index 2" (1987). They are all topologically equivalent to toroid
s. Their construction, by arranging n faces around each vertex, can be repeated indefinitely as tilings of the hyperbolic plane
. In the diagrams below, the hyperbolic tiling images have colors corresponding to those of the polyhedra images (except for the ditrigonal dodecadodecahedron
, where the correct image is not available yet).
Another group of regular abstract polyhedra comprise tilings of the real projective plane
. These include the hemicube
, hemi-octahedron
, hemi-dodecahedron
, and hemi-icosahedron
. They are (globally) projective polyhedra, and are the projective counterparts of the Platonic solid
s.
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
whose faces are congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
regular polygons which are assembled in the same way around each vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
and face-transitive - i.e. it is transitive on its flags. This last alone is a sufficient definition.
A regular polyhedron is identified by its Schläfli symbol of the form {n, m}, where n is the number of sides of each face and m the number of faces meeting at each vertex. There are 5 finite regular polyhedra, which are called the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, the self-dual tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
{3,3}, dual-pair cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
/octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
{4,3}, and dual pair dodecahedron/icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
{5,3}.
The regular polyhedra
There are five convexConvex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
regular polyhedra, known as the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s:
Platonic solids
 |
 |
 |
 |
 |
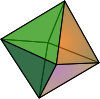
| Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... {3, 3} |
Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... {4, 3} |
Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... {3, 4} |
Dodecahedron {5, 3} | Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... {3, 5} |
Kepler-Poinsot polyhedra
and four regular star polyhedraStar polyhedron
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
, the Kepler-Poinsot polyhedra:
 |
 |
 |
 |
| Small stellated dodecahedron {5/2, 5} |
Great dodecahedron {5, 5/2} |
Great stellated dodecahedron {5/2, 3} |
Great icosahedron {3, 5/2} |
Characteristics
Equivalent propertiesThe property of having a similar arrangement of faces around each vertex can be replaced by any of the following equivalent conditions in the definition:
- The vertices of the polyhedron all lie on a sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. - All the dihedral angleDihedral angleIn geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
s of the polyhedron are equal. - All the vertex figureVertex figureIn geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s of the polyhedron are regular polygonRegular polygonA regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s. - All the solid angleSolid angleThe solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
s of the polyhedron are congruent. (Cromwell, 1997)
Concentric spheres
A regular polyhedron has all of three related spheres (other polyhedra lack at least one kind) which share its centre:
- An insphere, tangent to all faces.
- An intersphere or midsphereMidsphereIn geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point...
, tangent to all edges. - A circumsphere, tangent to all vertices.
Symmetry
The regular polyhedra are the most symmetrical
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of all the polyhedra. They lie in just three symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
s, which are named after them:
- Tetrahedral
- Octahedral (or cubic)
- Icosahedral (or dodecahedral)
Any shapes with icosahedral or octahedral symmetry will also contain tetrahedral symmetry.
Euler characteristic
The five Platonic solids have an Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of 2. Some of the regular stars have a different value.
Duality of the regular polyhedra
The regular polyhedra come in natural pairs, with each twin being dualDual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
to the other (i.e. the vertices of one polyhedron correspond to the faces of the other, and vice versa):
- The tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
is self-dual, i.e. it pairs with itself. - The cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
and octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
are dual to each other. - The icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
and dodecahedron are dual to each other. - The small stellated dodecahedron and great dodecahedron are dual to each other.
- The great stellated dodecahedron and great icosahedron are dual to each other.
The Schläfli symbol of the dual is just the original written backwards, for example the dual of {5, 3} is {3, 5}.
For further information please see the individual articles or the general polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
article.
History
See also Regular polytope: History of discovery.Prehistory
Stones carved in shapes showing the symmetry of all five of the Platonic solids have been found in ScotlandScotland
Scotland is a country that is part of the United Kingdom. Occupying the northern third of the island of Great Britain, it shares a border with England to the south and is bounded by the North Sea to the east, the Atlantic Ocean to the north and west, and the North Channel and Irish Sea to the...
and may be as much as 4,000 years old. These stones show not only the form of each of the five Platonic solids, but also the relations of duality amongst them (that is, that the centres of the faces of the cube gives the vertices of an octahedron, and so on). Examples of these stones are on display in the John Evans room of the Ashmolean Museum
Ashmolean Museum
The Ashmolean Museum on Beaumont Street, Oxford, England, is the world's first university museum...
at Oxford University. Why these objects were made, or how their creators gained the inspiration for them, is a mystery.
It is also possible that the Etruscans
Etruscan civilization
Etruscan civilization is the modern English name given to a civilization of ancient Italy in the area corresponding roughly to Tuscany. The ancient Romans called its creators the Tusci or Etrusci...
preceded the Greeks in their awareness of at least some of the regular polyhedra, as evidenced by the discovery near Padua
Padua
Padua is a city and comune in the Veneto, northern Italy. It is the capital of the province of Padua and the economic and communications hub of the area. Padua's population is 212,500 . The city is sometimes included, with Venice and Treviso, in the Padua-Treviso-Venice Metropolitan Area, having...
(in Northern Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
) in the late 19th century of a dodecahedron made of soapstone
Soapstone
Soapstone is a metamorphic rock, a talc-schist. It is largely composed of the mineral talc and is thus rich in magnesium. It is produced by dynamothermal metamorphism and metasomatism, which occurs in the areas where tectonic plates are subducted, changing rocks by heat and pressure, with influx...
, and dating back more than 2,500 years (Lindemann, 1987). Pyritohedric crystals are found in northern Italy.
Greeks
The earliest known written records of the regular convex solids originated from Classical Greece. When these solids were all discovered and who by is not known, but TheaetetusTheaetetus (mathematician)
Theaetetus, Theaitētos, of Athens, possibly son of Euphronius, of the Athenian deme Sunium, was a classical Greek mathematician...
, (an Athenian
Athens
Athens , is the capital and largest city of Greece. Athens dominates the Attica region and is one of the world's oldest cities, as its recorded history spans around 3,400 years. Classical Athens was a powerful city-state...
), was the first to give a mathematical description of all five (Van der Waerden, 1954), (Euclid, book XIII). H.S.M. Coxeter (Coxeter, 1948, Section 1.9) credits Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
(400 BC) with having made models of them, and mentions that one of the earlier Pythagoreans, Timaeus of Locri
Timaeus of Locri
Timaeus of Locri was a Greek Pythagorean philosopher living in the 5th century BC.He features in Plato's Timaeus, where he is said to come from Locri in Italy, thus of Locrian origin.He also appears as one of the speakers in Plato's Critias....
, used all five in a correspondence between the polyhedra and the nature of the universe as it was then perceived - this correspondence is recorded in Plato's dialogue Timaeus
Timaeus (dialogue)
Timaeus is one of Plato's dialogues, mostly in the form of a long monologue given by the title character, written circa 360 BC. The work puts forward speculation on the nature of the physical world and human beings. It is followed by the dialogue Critias.Speakers of the dialogue are Socrates,...
. Euclid's reference to Plato led to their common description as the Platonic solids.
One might characterise the Greek definition as follows:
- A regular polygon is a (convexConvex polygonIn geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
) planar figure with all edges equal and all corners equal - A regular polyhedron is a solid (convex) figure with all faces being congruent regular polygons, the same number arranged all alike around each vertex.
This definition rules out, for example, the square pyramid
Square pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
(since although all the faces are regular, the square base is not congruent to the triangular sides), or the shape formed by joining two tetrahedra together (since although all faces of that triangular bipyramid would be equilateral triangles, that is, congruent and regular, some vertices have 3 triangles and others have 4).
This concept of a regular polyhedron would remain unchallenged for almost 2000 years.
Regular star polyhedra
Regular star polygons such as the pentagramPentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
(star pentagon) were also known to the ancient Greeks - the pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
was used by the Pythagoreans as their secret sign, but they did not use them to construct polyhedra. It was not until the early 17th century that Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
realised that pentagrams could be used as the faces of regular star polyhedra
Star polyhedron
In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
. Some of these star polyhedra may have been discovered by others before Kepler's time, but Kepler was the first to recognise that they could be considered "regular" if one removed the restriction that regular polyhedra be convex. Two hundred years later Louis Poinsot
Louis Poinsot
Louis Poinsot was a French mathematician and physicist. Poinsot was the inventor of geometrical mechanics, showing how a system of forces acting on a rigid body could be resolved into a single force and a couple.-Life:...
also allowed star vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s (circuits around each corner), enabling him to discover two new regular star polyhedra along with rediscovering Kepler's. These four are the only regular star polyhedra, and have come to be known as the Kepler-Poinsot polyhedra. It was not until the mid-19th century, several decades after Poinsot published, that Cayley gave them their modern English names: (Kepler's) small stellated dodecahedron and great stellated dodecahedron, and (Poinsot's) great icosahedron and great dodecahedron.
The Kepler-Poinsot polyhedra may be constructed from the Platonic solids by a process called stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
. The reciprocal process to stellation is called facetting
Facetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
(or faceting). Every stellation of one polyhedron is dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
, or reciprocal, to some facetting of the dual polyhedron. The regular star polyhedra can also be obtained by facetting the Platonic solids. This was first done by Bertrand around the same time that Cayley named them.
By the end of the 19th century there were therefore nine regular polyhedra - five convex and four star.
Regular polyhedra in nature
Each of the Platonic solids occurs naturally in one form or another.The tetrahedron, cube, and octahedron all occur as crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s. These by no means exhaust the numbers of possible forms of crystals (Smith, 1982, p212), of which there are 48. Neither the regular icosahedron nor the regular dodecahedron are amongst them, although one of the forms, called the pyritohedron
Pyritohedron
In geometry, a pyritohedron is an irregular dodecahedron with pyritohedral symmetry. Like the regular dodecahedron, it has twelve identical pentagonal faces, with three meeting in each of the 20 vertices. However, the pentagons are not regular, and the structure has no fivefold symmetry axes...
, has twelve pentagonal faces arranged in the same pattern as the faces of the regular dodecahedron. The faces of the pyritohedron are, however, not regular, so the pyritohedron is also not regular.
Ernst Haeckel
The "European War" became known as "The Great War", and it was not until 1920, in the book "The First World War 1914-1918" by Charles à Court Repington, that the term "First World War" was used as the official name for the conflict.-Research:...
described a number of species of Radiolaria, some of whose skeletons are shaped like various regular polyhedra. (Haeckel, 1904) Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra; the shapes of these creatures are indicated by their names. The outer protein shells of many virus
Virus
A virus is a small infectious agent that can replicate only inside the living cells of organisms. Viruses infect all types of organisms, from animals and plants to bacteria and archaea...
es form regular polyhedra. For example, HIV
HIV
Human immunodeficiency virus is a lentivirus that causes acquired immunodeficiency syndrome , a condition in humans in which progressive failure of the immune system allows life-threatening opportunistic infections and cancers to thrive...
is enclosed in a regular icosahedron.
A more recent discovery is of a series of new types of carbon
Carbon
Carbon is the chemical element with symbol C and atomic number 6. As a member of group 14 on the periodic table, it is nonmetallic and tetravalent—making four electrons available to form covalent chemical bonds...
molecule, known as the fullerene
Fullerene
A fullerene is any molecule composed entirely of carbon, in the form of a hollow sphere, ellipsoid, or tube. Spherical fullerenes are also called buckyballs, and they resemble the balls used in association football. Cylindrical ones are called carbon nanotubes or buckytubes...
s (see (Curl, 1991) for an exposition of this discovery). Although C60, the most easily produced fullerene, looks more or less spherical, some of the larger varieties (such as C240, C480 and C960) are hypothesised to take on the form of slightly rounded icosahedra, a few nanometres across.
In ancient times the Pythagoreans
Pythagoreanism
Pythagoreanism was the system of esoteric and metaphysical beliefs held by Pythagoras and his followers, the Pythagoreans, who were considerably influenced by mathematics. Pythagoreanism originated in the 5th century BCE and greatly influenced Platonism...
believed that there was a harmony between the regular polyhedra and the orbits of the planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
s. In the 17th century, Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
studied data on planetary motion compiled by Tycho Brahe
Tycho Brahe
Tycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
and for a decade tried to establish the Pythagorean ideal by finding a match between the sizes of the polyhedra and the sizes of the planets' orbits. His search failed in its original objective, but out of this research came Kepler's discoveries of the Kepler solids as regular polytopes, the realisation that the orbits of planets are not circles, and the laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
for which he is now famous. In Kepler's time only five planets (excluding the earth) were known, nicely matching the number of Platonic solids. Kepler's work, and the discovery since that time of Uranus
Uranus
Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus...
and Neptune
Neptune
Neptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times...
, have invalidated the Pythagorean idea.
Around the same time as the Pythagoreans, Plato described a theory of matter in which the five elements (earth, air, fire, water and spirit) each comprised tiny copies of one of the five regular solids. Matter was built up from a mixture of these polyhedra, with each substance having different proportions in the mix. Two thousand years later Dalton's atomic theory would show this idea to be along the right lines, though not related directly to the regular solids.
Further generalisations
The 20th century saw a succession of generalisations of the idea of a regular polyhedron, leading to several new classes.Regular skew polyhedra
In the first decades, Coxeter and Petrie allowed "saddle" vertices with alternating ridges and valleys, enabling them to construct three infinite folded surfaces which they called regular skew polyhedraRegular skew polyhedron
In geometry, the regular skew polyhedra are generalizations to the set of regular polyhedron which include the possibility of nonplanar faces or vertex figures....
. Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
, with m regular l-gons around a vertex. The n defines n-gonal holes. Their vertex figures are regular skew polygons, vertices zig-zagging between two planes.
| Infinite regular skew polyhedra in 3-space (partially drawn) | ||
|---|---|---|
 {4,6|4} |
 {6,4|4} |
 {6,6|3} |
Finite regular skew polyhedra exist in 4-space. These finite regular skew polyhedra in 4-space can be seen as a subset of the faces of uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
s. Two dual solutions are related to the 5-cell, two dual solutions are related to the 24-cell, and an infinite set of self-dual duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
s generate regular skew polyhedra as {4, 4 | n}. In the infinite limit these approach a duocylinder and look like a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
in their stereographic projection
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
s into 3-space.
| Orthogonal Coxeter plane projections | Stereographic projection Stereographic projection The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it... |
|||
|---|---|---|---|---|
| A4 | F4 | |||
| {4, 6 | 3} | {6, 4 | 3} | {4, 8 | 3} | {8, 4 | 3} | {4, 4 | n} |
Regular polyhedra in non-Euclidean spaces
Studies of non-Euclidean hyperbolicHyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, elliptic and complex
Complex space
In mathematics, n-dimensional complex space is a multi-dimensional generalisation of the complex numbers, which have both real and imaginary parts or dimensions...
spaces, discovered over the preceding century, led to the discovery of more new polyhedra such as complex polyhedra
Complex polytope
A complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one....
which could only take regular geometric form in those spaces.
Abstract regular polyhedra
By now, polyhedra were firmly understood as three-dimensional examples of more general polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s in any number of dimensions. The second half of the century saw the development of abstract algebraic ideas such as Polyhedral combinatorics
Polyhedral combinatorics
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher dimensional convex polytopes....
, culminating in the idea of an abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
as a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
(poset) of elements. The elements of an abstract polyhedron are its body (the maximal element), its faces, edges, vertices and the null polytope or empty set. These abstract elements can be mapped into ordinary space or realised as geometrical figures. Some abstract polyhedra have well-formed or faithful realisations, others do not. A flag is a connected set of elements of each dimension - for a polyhedron that is the body, a face, an edge of the face, a vertex of the edge, and the null polytope. An abstract polytope is said to be regular if its combinatorial symmetries are transitive on its flags - that is to say, that any flag can be mapped onto any other under a symmetry of the polyhedron. Abstract regular polytopes remain an active area of research.
Five such regular abstract polyhedra, which can not be realised faithfully, were identified by H. S. M. Coxeter in his book Regular Polytopes (1977) and again by J. M. Wills in his paper "The combinatorially regular polyhedra of index 2" (1987). They are all topologically equivalent to toroid
Toroid
Toroid may refer to*Toroid , a doughnut-like solid whose surface is a torus.*Toroidal inductors and transformers which have wire windings on circular ring shaped magnetic cores.*Vortex ring, a toroidal flow in fluid mechanics....
s. Their construction, by arranging n faces around each vertex, can be repeated indefinitely as tilings of the hyperbolic plane
Hyperbolic plane
In mathematics, the term hyperbolic plane may refer to:* A two-dimensional plane in hyperbolic geometry* A two-dimensional plane in Minkowski space...
. In the diagrams below, the hyperbolic tiling images have colors corresponding to those of the polyhedra images (except for the ditrigonal dodecadodecahedron
Ditrigonal dodecadodecahedron
In geometry, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41.- Related polyhedra :Its convex hull is a regular dodecahedron...
, where the correct image is not available yet).
| Polyhedron | Medial rhombic triacontahedron Medial rhombic triacontahedron In geometry, the medial rhombic triacontahedron is a nonconvex isohedral polyhedron. It is the dual of the dodecadodecahedron. It has 30 intersecting rhombic faces.It can also be called the small stellated triacontahedron.... |
 Dodecadodecahedron |
Medial triambic icosahedron |
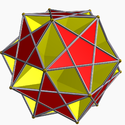 Ditrigonal dodecadodecahedron Ditrigonal dodecadodecahedron In geometry, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41.- Related polyhedra :Its convex hull is a regular dodecahedron... |
Excavated dodecahedron Excavated dodecahedron In geometry, the excavated dodecahedron is a star polyhedron. Its exterior surface represents the Ef1g1 stellation of the icosahedron. Magnus Wenninger list it in his Polyhedran models book as model 28, and calls it the third stellation of icosahedron.It is also a facetting of the dodecahedron... |
|---|---|---|---|---|---|
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... |
{5}, {5/2} |
(5.5/2)2 |
{5}, {5/2} |
(5.5/3)3 |
|
| Faces | 30 rhombi |
12 pentagons 12 pentagram |
20 hexagons |
12 pentagons 12 pentagrams |
20 hexagons |
| Tiling |  {4, 5} |
 {5, 4} |
{6, 5} |
 {5, 6} |
{6, 6} |
Another group of regular abstract polyhedra comprise tilings of the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
. These include the hemicube
Hemi-cube (geometry)
In abstract geometry, a hemi-cube is an abstract regular polyhedron, containing half the faces of a cube.It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing...
, hemi-octahedron
Hemi-octahedron
A hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron.It has 4 triangular faces, 6 edges, and 3 vertices...
, hemi-dodecahedron
Hemi-dodecahedron
A hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and...
, and hemi-icosahedron
Hemi-icosahedron
A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing...
. They are (globally) projective polyhedra, and are the projective counterparts of the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s.
 Hemi-cube {4,3} |
Hemi-octahedron Hemi-octahedron A hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron.It has 4 triangular faces, 6 edges, and 3 vertices... {3,4} |
Hemi-dodecahedron Hemi-dodecahedron A hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and... {3,5} |
Hemi-icosahedron Hemi-icosahedron A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing... {5,3} |
See also
- Quasiregular polyhedronQuasiregular polyhedronIn geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
- Semiregular polyhedronSemiregular polyhedronThe term semiregular polyhedron is used variously by different authors.In its original definition, it is a polyhedron with regular faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron...
- Uniform polyhedronUniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
- Regular polytopeRegular polytopeIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...