
Regular skew polyhedron
Encyclopedia
In geometry
, the regular skew polyhedra are generalizations to the set of regular polyhedron
which include the possibility of nonplanar faces
or vertex figure
s.
These polyhedra have two forms: infinite polyhedra that span 3-space, and finite polyhedra that close into 4-space.
Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure
, m l-gons around a vertex, and n-gonal holes. Their vertex figures are skew polygon
s, zig-zagging between two planes.
The regular skew polyhedra, reresented by {l,m|n}, follow this equation:
Also solutions to the equation above are the Euclidean regular tilings {3,6}, {6,3}, {4,4}, represented as {3,6|6}, {6,3|6}, and {4,4|∞}.
Here are some partial representations, vertical projected views of their skew vertex figures, and partial corresponding uniform honeycombs.
Coxeter also ennumerated the a larger set of finite regular polyhedra in his paper "regular skew polyhedra in three and four dimensions, and their topological analogues".
Just like the infinite skew polyhedra represent manifold surfaces between the cells of the convex uniform honeycomb
s, the finite forms all represent manifold surfaces within the cells of the uniform polychora
.
A first form, {l, m | n}, repeats the five convex Platonic solid
s, and one nonconvex Kepler-Poinsot solid
:
The remaining solutions of the first form, {l, m | n} exist in 4-space. Polyhedra of the form {l, m | n} have a cyclic Coxeter group
symmetry of [(l/2,n,m/2,n)], which reduces to the linear [n,l/2,n] when m is 4, and [n,m,/2,n] when l=4. {4,4|n} produces a double n-prism, or n-n duoprism
, and specifically {4,4|4} fits inside of a {4}x{4} tesseract
. {a,4|b} is represented by the {a} faces of the bitruncated {b,a/2,b} uniform polychoron
, and {4,a|b} is represented by square faces of the runcinated {b,a/2,b}.
A final set is based on Coxeter's further extended form {q1,m|q2,q3...} or with q2 unspecified: {l, m |, q}.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the regular skew polyhedra are generalizations to the set of regular polyhedron
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
which include the possibility of nonplanar faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
or vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s.
These polyhedra have two forms: infinite polyhedra that span 3-space, and finite polyhedra that close into 4-space.
History
According to Coxeter, in 1926 John Flinders Petrie generalized the concept of regular skew polygons (nonplanar polygons) to regular skew polyhedra.Coxeter offered a modified Schläfli symbol {l,m|n} for these figures, with {l,m} implying the vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
, m l-gons around a vertex, and n-gonal holes. Their vertex figures are skew polygon
Skew polygon
In geometry, a skew polygon is a polygon whose vertices do not lie in a plane. Skew polygons must have at least 4 vertices.A regular skew polygon is a skew polygon with equal edge lengths and which is vertex-transitive....
s, zig-zagging between two planes.
The regular skew polyhedra, reresented by {l,m|n}, follow this equation:
- 2*sin(π/l)*sin(π/m)=cos(π/n)
Infinite regular skew polyhedra
There are 3 regular skew polyhedra, the first two being duals:- {4,6|4}: 6 squareSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s on a vertex (related to cubic honeycombCubic honeycombThe cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
, constructed by cubic cells, removing two opposite faces from each, and linking sets of six together around a faceless cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
.) - {6,4|4}: 4 hexagons on a vertex (related to bitruncated cubic honeycombBitruncated cubic honeycombThe bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra.It is one of 28 uniform honeycombs. It has 4 truncated octahedra around each vertex....
, constructed by truncated octahedronTruncated octahedronIn geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....
with their square faces removed and linking hole pairs of holes together.) - {6,6|3}: 6 hexagons on a vertex (related to quarter cubic honeycombQuarter cubic honeycombThe quarter cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1...
, constructed by truncated tetrahedronTruncated tetrahedronIn geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :...
cells, removing triangle faces, and linking sets of four around a faceless tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
.)
Also solutions to the equation above are the Euclidean regular tilings {3,6}, {6,3}, {4,4}, represented as {3,6|6}, {6,3|6}, and {4,4|∞}.
Here are some partial representations, vertical projected views of their skew vertex figures, and partial corresponding uniform honeycombs.
| Partial polyhedra | ||
|---|---|---|
 {4,6|4} |
 {6,4|4} |
 {6,6|3} |
| Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:... s |
||
{4,6} |
{6,4} |
{6,6} |
| Related convex uniform honeycomb Convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;... s |
||
 Runcinated cubic honeycomb Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.... t0,3{4,3,4} |
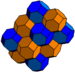 Bitruncated cubic Bitruncated cubic honeycomb The bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra.It is one of 28 uniform honeycombs. It has 4 truncated octahedra around each vertex.... t1,2{4,3,4} |
quarter cubic honeycomb Quarter cubic honeycomb The quarter cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1... t0,1{3[4]} |
Finite regular skew polyhedra of 4-space
| A4 Coxeter plane projections | |
|---|---|
| {4, 6 | 3} | {6, 4 | 3} |
| Runcinated 5-cell (60 edges, 20 vertices) |
Bitruncated 5-cell (60 edges, 30 vertices) |
| F4 Coxeter plane projections | |
| {4, 8 | 3} | {8, 4 | 3} |
| Runcinated 24-cell Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... (576 edges, 144 vertices) |
Bitruncated 24-cell (576 edges, 288 vertices) |
| Some of the 4-dimensional regular skew polyhedra fits inside the uniform polychora as shown in these projections. | |
Coxeter also ennumerated the a larger set of finite regular polyhedra in his paper "regular skew polyhedra in three and four dimensions, and their topological analogues".
Just like the infinite skew polyhedra represent manifold surfaces between the cells of the convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
s, the finite forms all represent manifold surfaces within the cells of the uniform polychora
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
.
A first form, {l, m | n}, repeats the five convex Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, and one nonconvex Kepler-Poinsot solid
Kepler-Poinsot solid
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures....
:
| {l, m | n} | Faces | Edges | Vertices | p | Polyhedron Polyhedron In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges... |
Symmetry order |
|---|---|---|---|---|---|---|
| {3,3| 3} = {3,3} | 4 | 6 | 4 | 0 | Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
12 |
| {3,4| 4} = {3,4} | 8 | 12 | 6 | 0 | Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
24 |
| {4,3| 4} = {4,3} | 6 | 12 | 8 | 0 | Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
24 |
| {3,5| 5} = {3,5} | 20 | 30 | 12 | 0 | Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
60 |
| {5,3| 5} = {5,3} | 12 | 30 | 20 | 0 | Dodecahedron | 60 |
| {5,5| 3} = {5,5/2} | 12 | 30 | 12 | 4 | Great dodecahedron | 60 |
The remaining solutions of the first form, {l, m | n} exist in 4-space. Polyhedra of the form {l, m | n} have a cyclic Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
symmetry of [(l/2,n,m/2,n)], which reduces to the linear [n,l/2,n] when m is 4, and [n,m,/2,n] when l=4. {4,4|n} produces a double n-prism, or n-n duoprism
Duoprism
In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher...
, and specifically {4,4|4} fits inside of a {4}x{4} tesseract
Tesseract
In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8...
. {a,4|b} is represented by the {a} faces of the bitruncated {b,a/2,b} uniform polychoron
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
, and {4,a|b} is represented by square faces of the runcinated {b,a/2,b}.
| {l, m | n} | Faces | Edges | Vertices | p | Structure | Symmetry | Order | Related uniform polychora Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
|---|---|---|---|---|---|---|---|---|
| {4,4| 3} | 9 | 18 | 9 | 1 | D3xD3 | [3,2,3] | 18 | 3-3 duoprism Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
| {4,4| 4} | 16 | 32 | 16 | 1 | D4xD4 | [4,2,4] | 32 | 4-4 duoprism or tesseract Tesseract In geometry, the tesseract, also called an 8-cell or regular octachoron or cubic prism, is the four-dimensional analog of the cube. The tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of 6 square faces, the hypersurface of the tesseract consists of 8... |
| {4,4| 5} | 25 | 50 | 25 | 1 | D5xD5 | [5,2,5] | 50 | 5-5 duoprism Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
| {4,4| 6} | 36 | 72 | 36 | 1 | D6xD6 | [6,2,6] | 72 | 6-6 duoprism Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
| {4,4| n} | n2 | 2n2 | n2 | 1 | DnxDn | [n,2,n] | 2n2 | n-n duoprism Duoprism In geometry of 4 dimensions or higher, a duoprism is a polytope resulting from the Cartesian product of two polytopes, each of two dimensions or higher... |
| {4,6| 3} | 30 | 60 | 20 | 6 | S5 Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... |
[3,3,3] | 120 | Runcinated 5-cell |
| {6,4| 3} | 20 | 60 | 30 | 6 | S5 Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... |
[3,3,3] | 120 | Bitruncated 5-cell |
| {4,8| 3} | 288 | 576 | 144 | 73 | [3,4,3] | 1152 | Runcinated 24-cell Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell.... |
|
| {8,4| 3} | 144 | 576 | 288 | 73 | [3,4,3] | 1152 | Bitruncated 24-cell |
| {l, m | n} | Faces | Edges | Vertices | p | Structure | Symmetry | Order | Related uniform polychora Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra.... |
|---|---|---|---|---|---|---|---|---|
| {4,5| 5} | 90 | 180 | 72 | 10 | A6 | [5,5/2,5] | 360 | Runcinated grand stellated 120-cell |
| {5,4| 5} | 72 | 180 | 90 | 10 | A6 | [5,5/2,5] | 360 | Bitruncated grand stellated 120-cell |
| {l, m | n} | Faces | Edges | Vertices | p | Structure | Order |
|---|---|---|---|---|---|---|
| {4,5| 4} | 40 | 80 | 32 | 5 | ? | 160 |
| {5,4| 4} | 32 | 80 | 40 | 5 | ? | 160 |
| {4,7| 3} | 42 | 84 | 24 | 10 | LF(2,7) | 168 |
| {7,4| 3} | 24 | 84 | 42 | 10 | LF(2,7) | 168 |
| {5,5| 4} | 72 | 180 | 72 | 19 | A6 | 360 |
| {6,7| 3} | 182 | 546 | 156 | 105 | LF(2,13) General linear group In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible... |
1092 |
| {7,6| 3} | 156 | 546 | 182 | 105 | LF(2,13) | 1092 |
| {7,7| 3} | 156 | 546 | 156 | 118 | LF(2,13) | 1092 |
| {4,9| 3} | 612 | 1224 | 272 | 171 | LF(2,17) | 2448 |
| {9,4| 3} | 272 | 1224 | 612 | 171 | LF(2,17) | 2448 |
| {7,8| 3} | 1536 | 5376 | 1344 | 1249 | ? | 10752 |
| {8,7| 3} | 1344 | 5376 | 1536 | 1249 | ? | 10752 |
A final set is based on Coxeter's further extended form {q1,m|q2,q3...} or with q2 unspecified: {l, m |, q}.
| {l, m |, q} | Faces | Edges | Vertices | p | Structure | Order |
|---|---|---|---|---|---|---|
| {3,6|,q} | 2q2 | 3q2 | q2 | 1 | ? | 2q2 |
| {3,2q|,3} | 2q2 | 3q2 | 3q | (q-1)*(q-2)/2 | ? | 2q2 |
| {3,7|,4} | 56 | 84 | 24 | 3 | LF(2,7) General linear group In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible... |
168 |
| {3,8|,4} | 112 | 168 | 42 | 8 | PGL(2,7) Projective linear group In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P... |
336 |
| {4,6|,3} | 84 | 168 | 56 | 15 | PGL(2,7) Projective linear group In mathematics, especially in the group theoretic area of algebra, the projective linear group is the induced action of the general linear group of a vector space V on the associated projective space P... |
336 |
| {3,7|,6} | 364 | 546 | 156 | 14 | LF(2,13) General linear group In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible... |
1092 |
| {3,7|,7} | 364 | 546 | 156 | 14 | LF(2,13) | 1092 |
| {3,8|,5} | 720 | 1080 | 270 | 46 | ? | 2160 |
| {3,10|,4} | 720 | 1080 | 216 | 73 | ? | 2160 |
| {4,6|,2} | 12 | 24 | 8 | 3 | S4 Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... xS2 |
48 |
| {5,6|,2} | 24 | 60 | 20 | 9 | A5xS2 | 120 |
| {3,11|,4} | 2024 | 3036 | 552 | 231 | LF(2,23) | 6072 |
| {3,7|,8} | 3584 | 5376 | 1536 | 129 | ? | 10752 |
| {3,9|,5} | 12180 | 18270 | 4060 | 1016 | LF(2,29)xA3 | 36540 |

