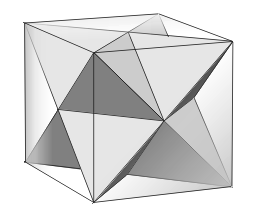
Stella octangula as a facetting of the cube

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, facetting (also spelled faceting) is the process of removing parts of a polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

, polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 or polytope

Polytope

In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...

, without creating any new vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

.

Facetting is the reciprocal or dual

Dual

Dual may refer to:* Dual , a notion of paired concepts that mirror one another** Dual , a formalization of mathematical duality** . . ...

 process to stellation

Stellation

Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...

. For every stellation of some convex polytope

Convex polytope

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

, there exists a dual facetting of the dual polytope.

For example the stellated dodecahedron and great icosahedron are two facettings of the icosahedron:

icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....	small stellated dodecahedron	great icosahedron

History

Facetting has not been studied as extensively as stellation

Stellation

Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...

.

• In 1619, Kepler
  Johannes Kepler
  Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
  
   described a regular
  Regular
  The term regular can mean normal or obeying rules. Regular may refer to:In organizations:* Regular Army for military usage* Regular clergy, members of a religious order subject to a rule of life* Regular Force for usage in the Canadian Forces...
  
   compound of two tetrahedra
  Tetrahedron
  In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
  
   which fits inside a cube, and which he called the Stella octangula
  Stella octangula
  The stellated octahedron, or stella octangula, is the only stellation of the octahedron. It was named by Johannes Kepler in 1609, though it was known to earlier geometers...
  
  . This seems to be the first known example of facetting.
• In 1858, Bertrand
  Joseph Louis François Bertrand
  Joseph Louis François Bertrand was a French mathematician who worked in the fields of number theory, differential geometry, probability theory, economics and thermodynamics....
  
   derived the regular star polyhedra
  Star polyhedron
  In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
  
   (Kepler-Poinsot polyhedra) by facetting the regular
  Regular
  The term regular can mean normal or obeying rules. Regular may refer to:In organizations:* Regular Army for military usage* Regular clergy, members of a religious order subject to a rule of life* Regular Force for usage in the Canadian Forces...
  
   convex
  Convex polytope
  A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
  
   icosahedron
  Icosahedron
  In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
  
   and dodecahedron.
• In 1974, Bridge enumerated the more straightforward facettings of the regular
  Regular
  The term regular can mean normal or obeying rules. Regular may refer to:In organizations:* Regular Army for military usage* Regular clergy, members of a religious order subject to a rule of life* Regular Force for usage in the Canadian Forces...
  
   polyhedra, including those of the dodecahedron.
• In 2006, Inchbald described the basic theory of facetting diagrams for polyhedra. For some vertex, the diagram shows all the possible edges and facets (new faces) which may be used to form facettings of the original hull. It is dual
  Dual
  Dual may refer to:* Dual , a notion of paired concepts that mirror one another** Dual , a formalization of mathematical duality** . . ...
  
   to the dual polyhedron
  Dual polyhedron
  In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
  
  's stellation diagram, which shows all the possible edges and vertices for some face plane of the original core.