
Semiregular polyhedron
Encyclopedia
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
The term semiregular polyhedron (or semiregular polytope) is used variously by different authors.
In its original definition, it is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with regular
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
faces and a symmetry group which is transitive on its vertices, which is more commonly referred to today as a uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
(this follows from Thorold Gosset
Thorold Gosset
Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...
's 1900 definition of the more general semiregular polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
). These polyhedra include:
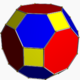
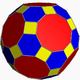
- The thirteen Archimedean solidArchimedean solidIn geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s. - An infinite series of convex prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s. - An infinite series of convex antiprismAntiprismIn geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s (their semiregular nature was first observed by Kepler).
These semiregular solids can be fully specified by a vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
, a listing of the faces by number of sides in order as they occur around a vertex. For example 3.5.3.5, represents the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
which alternates two triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s and two pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
s around each vertex. 3.3.3.5 in contrast is a pentagonal antiprism
Pentagonal antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
. These polyhedra are sometimes described as vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
.
Since Gosset
Thorold Gosset
Thorold Gosset was an English lawyer and an amateur mathematician. In mathematics, he is noted for discovering and classifying the semiregular polytopes in dimensions four and higher.According to H. S. M...
, other authors have used the term semiregular in different ways in relation to higher dimensional polytopes. E. L. Elte
E. L. Elte
Emanuel Lodewijk Elte was a Dutch mathematician. He is noted for discovering and classifying semiregular polytopes in dimensions four and higher....
provided a definition which Coxeter found too artificial. Coxeter himself dubbed Gosset's figures uniform
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
, with only a quite restricted subset classified as semiregular.
Yet others have taken the opposite path, categorising more polyhedra as semiregular. These include:
- Three sets of star polyhedraStar polyhedronIn geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....
which meet Gosset's definition, analogous to the three convex sets listed above. - The dualsDual polyhedronIn geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of the above semiregular solids, arguing that since the dual polyhedra share the same symmetries as the originals, they too should be regarded as semiregular. These duals include the Catalan solidCatalan solidIn mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s, the convex dipyramids and antidipyramids or trapezohedraTrapezohedronThe n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry...
, and their nonconvex analogues.
A further source of confusion lies in the way that the Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s are defined, again with different interpretations appearing.
Gosset's definition of semiregular includes figures of higher symmetry, the regular
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
and quasiregular
Quasiregular polyhedron
In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
polyhedra. Some later authors prefer to say that these are not semiregular, because they are more regular than that - the uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
are then said to include the regular, quasiregular and semiregular ones. This naming system works well, and reconciles many (but by no means all) of the confusions.
In practice even the most eminent authorities can get themselves confused, defining a given set of polyhedra as semiregular and/or Archimedean
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, and then assuming (or even stating) a different set in subsequent discussions. Assuming that one's stated definition applies only to convex polyhedra is probably the commonest failing. Coxeter, Cromwell and Cundy & Rollett are all guilty of such slips.
General remarks
In many works semiregular polyhedron is used as a synonym for Archimedean solidArchimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
. For example Cundy & Rollett (1961).
We can distinguish between the facially-regular and vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
figures based on Gosset, and their vertically-regular (or versi-regular) and facially-transitive duals.
Coxeter et al. (1954) use the term semiregular polyhedra to classify uniform polyhedra with Wythoff symbol
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
of the form p q | r, a definition encompassing only six of the Archimedean solids, as well as the regular prisms (but not the regular antiprisms) and numerous nonconvex solids. Later, Coxeter (1973) would quote Gosset's definition without comment, thus accepting it by implication.
Eric Weisstein, Robert Williams
Robert Williams (geometer)
Robert Edward Williams is an American designer, mathematician, and architect. He is noted for books on the geometry of natural structure, the discovery of a new space-filling polyhedron, the development of theoretical principles of Catenatic Geometry, and the invention of the Ars-Vivant Wild-life...
and others use the term to mean the convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
excluding the five regular polyhedra
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
-- including the Archimedean solids, the uniform prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
, and the uniform antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s (overlapping with the cube as a prism and regular octahedron as an antiprism).
Peter Cromwell (1997) writes in a footnote to Page 149 that, "in current terminology, 'semiregular polyhedra' refers to the Archimedean and Catalan
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
(Archimedean dual) solids". On Page 80 he describes the thirteen Archimedeans as semiregular, while on Pages 367 ff. he discusses the Catalans and their relationship to the 'semiregular' Archimedeans. By implication this treats the Catalans as not semiregular, thus effectively contradicting (or at least confusing) the definition he provided in the earlier footnote. He ignores nonconvex polyhedra.

