In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the dodecadodecahedron is a nonconvex uniform polyhedron

Nonconvex uniform polyhedron

In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...

, indexed as U₃₆. It is given a Schläfli symbol t₁{5/2,5}.

Net

A shape with the same exterior appearance as the dodecadodecahedron can be constructed by folding up these nets:
12 pentagrams and 20 rhombic

Rhombus

In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

 clusters are necessary. However, this construction replaces the crossing pentagonal faces of the dodecadodecahedron with non-crossing sets of rhombs, so it does not produce the same internal structure.

Related polyhedra

Its convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 is the icosidodecahedron

Icosidodecahedron

In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...

. It also shares its edge arrangement with the small dodecahemicosahedron

Small dodecahemicosahedron

In geometry, the small dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U62. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :...

 (having the pentagrammic faces in common), and with the great dodecahemicosahedron

Great dodecahemicosahedron

In geometry, the great dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U65. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :...

 (having the pentagonal faces in common).

Dodecadodecahedron	Small dodecahemicosahedron Small dodecahemicosahedron In geometry, the small dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U62. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :...	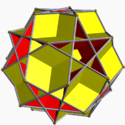Great dodecahemicosahedron Great dodecahemicosahedron In geometry, the great dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U65. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :...
Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...  (convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... )

This polyhedron can be considered a rectified

Rectification (geometry)

In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...

 great dodecahedron. It is center of a truncation sequence between a small stellated dodecahedron and great dodecahedron:

The truncated

Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...

 small stellated dodecahedron looks like a dodecahedron on the surface, but it has 24 faces: 12 pentagons from the truncated vertices and 12 overlapping as (truncated pentagrams). The truncation of the dodecadodecahedron itself is not uniform, but it has a uniform quasitruncation, the truncated dodecadodecahedron.

Name	Small stellated dodecahedron	Truncated small stellated dodecahedron	Dodecadodecahedron	Truncated great dodecahedron	Great dodecahedron
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
Picture

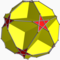
It is topologically equivalent to a quotient space

Quotient space

In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...

 of the hyperbolic

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

 order-4 pentagonal tiling, by distorting the pentagram

Pentagram

A pentagram is the shape of a five-pointed star drawn with five straight strokes...

s back into regular pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

s. As such, it is topologically a regular polyhedron

Regular polyhedron

A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

of index two:



The colours in the above image correspond to the red pentagrams and yellow pentagons of the dodecadodecahedron at the top of this article.

External links

• Uniform polyhedra and duals