In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron

Nonconvex uniform polyhedron

In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...

, indexed as U₄₁.

Related polyhedra

Its convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 is a regular dodecahedron. It additionally shares its edge arrangement with the small ditrigonal icosidodecahedron

Small ditrigonal icosidodecahedron

In geometry, the small ditrigonal icosidodecahedron is a nonconvex uniform polyhedron, indexed as U30.-Related polyhedra:Its convex hull is a regular dodecahedron...

 (having the pentagrammic faces in common), the great ditrigonal icosidodecahedron (having the pentagonal faces in common), and the regular compound of five cubes

Compound of five cubes

This polyhedral compound is a symmetric arrangement of five cubes. This compound was first described by Edmund Hess in 1876.It is one of five regular compounds, and dual to the compound of five octahedra....

.

Small ditrigonal icosidodecahedron Small ditrigonal icosidodecahedron In geometry, the small ditrigonal icosidodecahedron is a nonconvex uniform polyhedron, indexed as U30.-Related polyhedra:Its convex hull is a regular dodecahedron...	Great ditrigonal icosidodecahedron	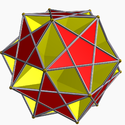Ditrigonal dodecadodecahedron
Dodecahedron (convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... )	Compound of five cubes Compound of five cubes This polyhedral compound is a symmetric arrangement of five cubes. This compound was first described by Edmund Hess in 1876.It is one of five regular compounds, and dual to the compound of five octahedra....

Furthermore, it may be viewed as a facetted

Facetting

In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...

 dodecahedron: the pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

al faces may be inscribed within the dodecahedron's pentagons. Its dual

Dual polyhedron

In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...

, the medial triambic icosahedron, is a stellation

Stellation

Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...

 of the icosahedron

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

.

It is topologically equivalent to the hyperbolic

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

 order-6 pentagonal tiling, by distorting the pentagram

Pentagram

A pentagram is the shape of a five-pointed star drawn with five straight strokes...

s back into regular pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

s. As such, it is a regular polyhedron

Regular polyhedron

A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...

of index two: