
Stellation
Encyclopedia
Stellation is a process of constructing new polygon
s (in two dimension
s), new polyhedra
in three dimensions, or, in general, new polytope
s in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again. The new figure is a stellation of the original.
A regular star polygon is represented by its Schläfli symbol {n/m}, where n is the number of vertices, m is the step used in sequencing the edges around it, and m and n are co-prime (i.e. have no common divisor
). Making m = 1 gives the convex {n}.
If n and m do have a common divisor, then a regular compound can be made. For example {6/2} leads to the regular compound of two triangles {3} or hexagram, while {10/4} leads to a compound of two pentagrams {5/2}.
Some authors use the Schläfli symbol for such regular compounds. Others regard the symbol as indicating a single path which is wound m times around n/m vertex points, such that one edge is superimposed upon another and each vertex point is visited m times. In this case a modified symbol may be used for the compound, for example 2{3} for the hexagram and 2{5/2) for the regular compound of two pentagrams.
A regular n-gon has (n-4)/2 stellations if n is even, and (n-3)/2 stellations if n is odd.
Like the heptagon, the octagon also has two octagram
mic stellations, one, {8/3} being a star polygon, and the other, {8/2}, being the compound of two squares
.
The face planes of a polyhedron divide space into many discrete cells. For a symmetrical polyhedron, these cells will fall into groups, or sets, of congruent cells - we say that the cells in such a congruent set are of the same type. A common method of finding stellations involves selecting one or more cell types.
This can lead to a huge number of possible forms, so further criteria are often imposed to reduce the set to those stellations that are significant and unique in some way.
A set of cells forming a closed layer around its core is called a shell. For a symmetrical polyhedron, a shell may be made up of one or more cell types.
Based on such ideas, several restrictive categories of interest have been identified.
We can also identify some other categories:
The Archimedean solids and their duals can also be stellated. Here we usually add the rule that all of the original face planes must be present in the stellation, i.e. we do not consider partial stellations. For example the cube
is not considered a stellation of the cuboctahedron
. There are:
Seventeen of the nonconvex uniform polyhedra are stellations of Archimedean solids.
, J.C.P. Miller proposed a set of rules for defining which stellation forms should be considered "properly significant and distinct".
These rules have been adapted for use with stellations of many other polyhedra. Under Miller's rules we find:
Many "Miller stellations" cannot be obtained directly by using Kepler's method. For example many have hollow centres where the original faces and edges of the core polyhedron are entirely missing: there is nothing left to be stellated. On the other hand, Kepler's method also yields stellations which are forbidden by Miller's rules since their cells are edge- or vertex-connected, even though their faces are single polygons. This discrepancy received no real attention until Inchbald (2002).
To the right is an example of a stellation. This one is a stellation of a Catalan solid
, the triakis icosahedron
.
As yet an alternative set of rules that takes this into account has not been fully developed. Most progress has been made based on the notion that stellation is the reciprocal process to facetting
, whereby parts are removed from a polyhedron without creating any new vertices. For every stellation of some polyhedron, there is a dual
facetting of the dual polyhedron
, and vice versa. By studying facettings of the dual, we gain insights into the stellations of the original. Bridge found his new stellation of the icosahedron by studying the facettings of its dual, the dodecahedron.
Some polyhedronists take the view that stellation is a two-way process, such that any two polyhedra sharing the same face planes are stellations of each other. This is understandable if one is devising a general algorithm suitable for use in a computer program, but is otherwise not particularly helpful.
Many examples of stellations can be found in the list of Wenninger's stellation models.
of an n-polytope exists in an (n-1)-dimensional hyperplane
of a given facet.
For example, in 4-space, the great grand stellated 120-cell is the final stellation of the Regular 4-polytope
120-cell.
's naming of the regular star polyhedra (nowadays known as the Kepler-Poinsot polyhedra). This system was widely, but not always systematically, adopted for other polyhedra and higher polytopes.
John Conway
devised a terminology for stellated polygon
s, polyhedra
and polychora
(Coxeter 1974). In this system the process of extending edges to create a new figure is called stellation, that of extending faces is called greatening and that of extending cells is called aggrandizement (this last does not apply to polyhedra). This allows a systematic use of words such as 'stellated', 'great, and 'grand' in devising names for the resulting figures. For example Conway proposed some minor variations to the names of the Kepler-Poinsot polyhedra.
of the uniform hemipolyhedra
.
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s (in two dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s), new polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
in three dimensions, or, in general, new polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again. The new figure is a stellation of the original.
Kepler's definition
In 1619 Kepler defined stellation for polygons and polyhedra, as the process of extending edges or faces until they meet to form a new polygon or polyhedron. He stellated the dodecahedron to obtain two of the regular star polyhedra (two of the Kepler-Poinsot polyhedra).Stellated polygons
A stellation of a regular polygon is a regular star polygon or polygonal compound.A regular star polygon is represented by its Schläfli symbol {n/m}, where n is the number of vertices, m is the step used in sequencing the edges around it, and m and n are co-prime (i.e. have no common divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
). Making m = 1 gives the convex {n}.
If n and m do have a common divisor, then a regular compound can be made. For example {6/2} leads to the regular compound of two triangles {3} or hexagram, while {10/4} leads to a compound of two pentagrams {5/2}.
Some authors use the Schläfli symbol for such regular compounds. Others regard the symbol as indicating a single path which is wound m times around n/m vertex points, such that one edge is superimposed upon another and each vertex point is visited m times. In this case a modified symbol may be used for the compound, for example 2{3} for the hexagram and 2{5/2) for the regular compound of two pentagrams.
A regular n-gon has (n-4)/2 stellations if n is even, and (n-3)/2 stellations if n is odd.
 The pentagram Pentagram A pentagram is the shape of a five-pointed star drawn with five straight strokes... , {5/2}, is the only stellation of a pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
 The hexagram, {6/2}, the stellation of a hexagon and a compound of two triangles. |
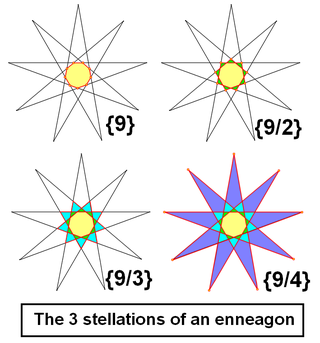 The enneagon Enneagon In geometry, a nonagon is a nine-sided polygon.The name "nonagon" is a prefix hybrid formation, from Latin , used equivalently, attested already in the 16th century in French nonogone and in English from the 17th century... (nonagon) has 3 enneagrammic Enneagram (geometry) In geometry, an enneagram is a nine-pointed geometric figure. It is sometimes called a nonagram.-Regular enneagram:A regular enneagram is constructed using the same points as the regular enneagon but connected in fixed steps... forms: {9/2}, {9/3}, {9/4}, with {9/3} being 3 triangles. |
  The heptagon has two heptagram Heptagram A heptagram or septegram is a seven-pointed star drawn with seven straight strokes.- Geometry :In general, a heptagram is any self-intersecting heptagon .... mic forms: {7/2}, {7/3} |
Like the heptagon, the octagon also has two octagram
Octagram
In geometry, an octagram is an eight-sided star polygon.- Geometry :In general, an octagram is any self-intersecting octagon ....
mic stellations, one, {8/3} being a star polygon, and the other, {8/2}, being the compound of two squares
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
.
Stellated polyhedra
 |
 |
 |
 |
 |
 |
 |
The face planes of a polyhedron divide space into many discrete cells. For a symmetrical polyhedron, these cells will fall into groups, or sets, of congruent cells - we say that the cells in such a congruent set are of the same type. A common method of finding stellations involves selecting one or more cell types.
This can lead to a huge number of possible forms, so further criteria are often imposed to reduce the set to those stellations that are significant and unique in some way.
A set of cells forming a closed layer around its core is called a shell. For a symmetrical polyhedron, a shell may be made up of one or more cell types.
Based on such ideas, several restrictive categories of interest have been identified.
- Main-line stellations. Adding successive shells to the core polyhedron leads to the set of main-line stellations.
- Fully supported stellations. The underside faces of a cell can appear externally as an "overhang." In a fully supported stellation there are no such overhangs, and all visible parts of a face are seen from the same side.
- Monoacral stellations. Literally "single-peaked." Where there is only one kind of peak, or vertex, in a stellation (i.e. all vertices are congruent within a single symmetry orbit), the stellation is monoacral. All such stellations are fully supported.
- Primary stellations. Where a polyhedron has planes of mirror symmetry, edges falling in these planes are said to lie in primary lines. If all edges lie in primary lines, the stellation is primary. All primary stellations are fully supported.
- Miller stellations. In "The Fifty-Nine Icosahedra" Coxeter, Du Val, Flather and Petrie record five rules suggested by MillerJ. C. P. MillerJeffrey Charles Percy Miller was an English mathematician and computing pioneer. He worked in number theory and on geometry, particularly polyhedra, where Miller's monster refers to the great dirhombicosidodecahedron....
. Although these rules refer specifically to the icosahedron's geometry, they can easily be adapted to work for arbitrary polyhedra. They ensure, among other things, that the rotational symmetry of the original polyhedron is preserved, and that each stellation is different in outward appearance. The four kinds of stellation just defined are all subsets of the Miller stellations.
We can also identify some other categories:
- A partial stellation is one where not all elements of a given dimensionality are extended.
- A sub-symmetric stellation is one where not all elements are extended symmetrically.
The Archimedean solids and their duals can also be stellated. Here we usually add the rule that all of the original face planes must be present in the stellation, i.e. we do not consider partial stellations. For example the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
is not considered a stellation of the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
. There are:
- 4 stellations of the rhombic dodecahedronRhombic dodecahedronIn geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
- 187 stellations of the triakis tetrahedronTriakis tetrahedronIn geometry, a triakis tetrahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated tetrahedron.It can be seen as a tetrahedron with triangular pyramids added to each face; that is, it is the Kleetope of the tetrahedron...
- 358,833,097 stellations of the rhombic triacontahedronRhombic triacontahedronIn geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
- 17 stellations of the cuboctahedronCuboctahedronIn geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
(4 are shown in Wenninger's "Polyhedron Models") - Unknown stellations of the icosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
, but many more than above! (19 are shown in Wenninger's "Polyhedron Models")
Seventeen of the nonconvex uniform polyhedra are stellations of Archimedean solids.
Miller's rules
In the book The fifty nine icosahedraThe fifty nine icosahedra
The Fifty Nine Icosahedra is a book written and illustrated by H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates the stellations of the regular convex or Platonic icosahedron, according to a set of rules put forward by J. C. P. Miller...
, J.C.P. Miller proposed a set of rules for defining which stellation forms should be considered "properly significant and distinct".
These rules have been adapted for use with stellations of many other polyhedra. Under Miller's rules we find:
- There are no stellations of the tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, because all faces are adjacent - There are no stellations of the cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, because non-adjacent faces are parallel and thus cannot be extended to meet in new edges - There is 1 stellation of the octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, the stella octangulaStella octangulaThe stellated octahedron, or stella octangula, is the only stellation of the octahedron. It was named by Johannes Kepler in 1609, though it was known to earlier geometers... - There are 3 stellations of the dodecahedron: the small stellated dodecahedron, the great dodecahedron and the great stellated dodecahedron, all of which are Kepler-Poinsot polyhedra.
- There are 58 stellations of the icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, including the great icosahedron (one of the Kepler-Poinsot polyhedra), and the second and finalFinal stellation of the icosahedronIn geometry, the complete or final stellation of the icosahedron is the outermost stellation of the icosahedron, and is "complete" and "final" because it includes all of the cells in the icosahedron's stellation diagram....
stellations of the icosahedron. The 59th model in "The fifty nine icosahedraThe fifty nine icosahedraThe Fifty Nine Icosahedra is a book written and illustrated by H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates the stellations of the regular convex or Platonic icosahedron, according to a set of rules put forward by J. C. P. Miller...
" is the original icosahedron itself.
Many "Miller stellations" cannot be obtained directly by using Kepler's method. For example many have hollow centres where the original faces and edges of the core polyhedron are entirely missing: there is nothing left to be stellated. On the other hand, Kepler's method also yields stellations which are forbidden by Miller's rules since their cells are edge- or vertex-connected, even though their faces are single polygons. This discrepancy received no real attention until Inchbald (2002).
To the right is an example of a stellation. This one is a stellation of a Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
, the triakis icosahedron
Triakis icosahedron
In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron...
.
Other rules for stellation
Miller's rules by no means represent the "correct" way to enumerate stellations. They are based on combining parts within the stellation diagram in certain ways, and don't take into account the topology of the resulting faces. As such there are some quite reasonable stellations of the icosahedron that are not part of their list - one was identified by James Bridge in 1974, while some "Miller stellations" are questionable as to whether they should be regarded as stellations at all - one of the icosahedral set comprises several quite disconnected cells floating symmetrically in space.As yet an alternative set of rules that takes this into account has not been fully developed. Most progress has been made based on the notion that stellation is the reciprocal process to facetting
Facetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
, whereby parts are removed from a polyhedron without creating any new vertices. For every stellation of some polyhedron, there is a dual
Dual
Dual may refer to:* Dual , a notion of paired concepts that mirror one another** Dual , a formalization of mathematical duality** . . ...
facetting of the dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
, and vice versa. By studying facettings of the dual, we gain insights into the stellations of the original. Bridge found his new stellation of the icosahedron by studying the facettings of its dual, the dodecahedron.
Some polyhedronists take the view that stellation is a two-way process, such that any two polyhedra sharing the same face planes are stellations of each other. This is understandable if one is devising a general algorithm suitable for use in a computer program, but is otherwise not particularly helpful.
Many examples of stellations can be found in the list of Wenninger's stellation models.
Stellated polytopes
The stellation process applies to higher dimensional polytopes as well. A stellation diagramStellation diagram
In geometry, a stellation diagram or stellation pattern is a two-dimensional diagram in the plane of some face of a polyhedron, showing lines where other face planes intersect with this one. The lines cause 2D space to be divided up into regions. Regions not intersected by any further lines are...
of an n-polytope exists in an (n-1)-dimensional hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
of a given facet.
For example, in 4-space, the great grand stellated 120-cell is the final stellation of the Regular 4-polytope
Regular 4-polytope
In geometry a regular 4-polytope can mean either a convex or nonconvex 4-polytope.See:* Convex regular 4-polytope - There are six convex regular polychora....
120-cell.
Naming stellations
The first systematic naming of stellated polyhedra was CayleyArthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
's naming of the regular star polyhedra (nowadays known as the Kepler-Poinsot polyhedra). This system was widely, but not always systematically, adopted for other polyhedra and higher polytopes.
John Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
devised a terminology for stellated polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s, polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
and polychora
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
(Coxeter 1974). In this system the process of extending edges to create a new figure is called stellation, that of extending faces is called greatening and that of extending cells is called aggrandizement (this last does not apply to polyhedra). This allows a systematic use of words such as 'stellated', 'great, and 'grand' in devising names for the resulting figures. For example Conway proposed some minor variations to the names of the Kepler-Poinsot polyhedra.
Stellation to infinity
Wenninger noticed that some polyhedra, such as the cube, do not have any finite stellations. The stellation cells are prisms which extend to infinity. The figure comprising these prisms is a stellation to infinity. By most definitions of a polyhedron, these stellations are not strictly polyhedra. They occur as dual polyhedraDual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of the uniform hemipolyhedra
Hemipolyhedron
In geometry, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron - hence the "hemi" prefix.The prefix "hemi"...
.
See also
- The fifty nine icosahedraThe fifty nine icosahedraThe Fifty Nine Icosahedra is a book written and illustrated by H. S. M. Coxeter, P. Du Val, H. T. Flather and J. F. Petrie. It enumerates the stellations of the regular convex or Platonic icosahedron, according to a set of rules put forward by J. C. P. Miller...
- List of Wenninger polyhedron models Includes 44 stellated forms of the octahedron, dodecahedron, icosahedron, and icosidodecahedron, enumerated the 1974 book "Polyhedron Models" by Magnus Wenninger
- Polyhedral compoundPolyhedral compoundA polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....
Includes 5 regular compounds and 4 dual regular compounds.
External links
- Stellating the Icosahedron and Facetting the Dodecahedron
- Stella: Polyhedron Navigator - Software for exploring polyhedra and printing nets for their physical construction. Includes uniform polyhedra, stellations, compounds, Johnson solids, etc.
- Enumeration of stellations
- Vladimir Bulatov Polyhedra Stellation.
- Stellation Applet
- An Interactive Creation of Polyhedra Stellations with Various Symmetries
- The Fifty-Nine Icosahedra - Applet
- 59 Stellations of the Icosahedron, George Hart
- Stellation: Beautiful Math
- Further Stellations of the Uniform Polyhedra, JOHN LAWRENCE HUDSON THE MATHEMATICAL INTELLIGENCER, Volume 31, Number 4, 2009

