Essential extension
Encyclopedia
In mathematics
, specifically module theory, given a ring
R and R-module
s M with a submodule N, the module M is said to be an essential extension of N (or N is said to be an essential submodule or large submodule of M) if for every submodule H of M,
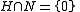implies that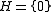 
The usual notations for essential extensions include the following two expressions: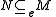
, and 
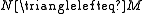
The dual
notion of an essential submodule is that of superfluous submodule (or small submodule). A submodule N is superfluous if for any other submodule H,
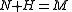implies that 
.
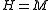The usual notations for superfluous submodules include: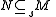
, and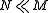 
Using Zorn's Lemma
it is possible to prove another useful fact:
For any submodule N of M, there exists a submodule C such that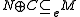
.
Furthermore, a module with no proper essential extension (that is, if the module is essential in another module, then it is equal to that module) is an injective module
. It is then possible to prove that every module M has a maximal essential extension E(M), called the injective hull
of M. The injective hull is necessarily an injective module, and is unique up to isomorphism. The injective hull is also minimal in the sense that any other injective module containing M contains a copy of E(M).
Many properties dualize to superfluous submodules, but not everything. Again with let M be a module, and K, N and H be submodules of M with K subset N.
Since every module can be mapped via a monomorphism
whose image is essential in an injective module (its injective hull), one might ask if the dual statement is true, i.e. for every module M, is there a projective module
P and an epimorphism
from P onto M whose kernel
is superfluous? (Such a P is called a projective cover
). The answer is "No" in general, and the special class of rings which provide their right modules projective covers is the class of right perfect ring
s.
C. An essential extension is a monomorphism
u : M → E such that for every non-zero subobject
s : N → E, the fibre product N ×E M ≠ 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically module theory, given a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R and R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s M with a submodule N, the module M is said to be an essential extension of N (or N is said to be an essential submodule or large submodule of M) if for every submodule H of M,
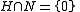implies that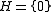 The usual notations for essential extensions include the following two expressions:
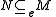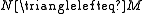
, and The dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
notion of an essential submodule is that of superfluous submodule (or small submodule). A submodule N is superfluous if for any other submodule H,
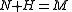implies that 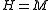.The usual notations for superfluous submodules include:
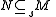, and 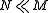Properties
Here are some of the elementary properties of essential extensions, given in the notation introduced above. Let M be a module, and K, N and H be submodules of M with K subset N- Clearly M is an essential submodule of M, and the zero submodule of a nonzero module is never essential.
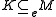if and only if 
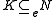and 
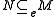
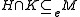if and only if 
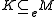and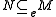 
Using Zorn's Lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
it is possible to prove another useful fact:
For any submodule N of M, there exists a submodule C such that
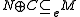.Furthermore, a module with no proper essential extension (that is, if the module is essential in another module, then it is equal to that module) is an injective module
Injective module
In mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
. It is then possible to prove that every module M has a maximal essential extension E(M), called the injective hull
Injective hull
In mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
of M. The injective hull is necessarily an injective module, and is unique up to isomorphism. The injective hull is also minimal in the sense that any other injective module containing M contains a copy of E(M).
Many properties dualize to superfluous submodules, but not everything. Again with let M be a module, and K, N and H be submodules of M with K subset N.
- The zero submodule is always superfluous, and a nonzero module M is never superfluous in itself.
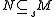if and only if 
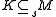and 
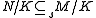
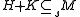if and only if 
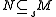and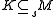 
.
Since every module can be mapped via a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
whose image is essential in an injective module (its injective hull), one might ask if the dual statement is true, i.e. for every module M, is there a projective module
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
P and an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
from P onto M whose kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
is superfluous? (Such a P is called a projective cover
Projective cover
In the branch of abstract mathematics called category theory, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual of injective envelopes.- Definition :...
). The answer is "No" in general, and the special class of rings which provide their right modules projective covers is the class of right perfect ring
Perfect ring
In the area of abstract algebra known as ring theory, a left perfect ring is a type of ring in which all left modules have projective covers. The right case is defined by analogy, and the condition is not left-right symmetric, that is, there exist rings which are perfect on one side but not the...
s.
Generalization
This definition can be generalized to an arbitrary abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
C. An essential extension is a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
u : M → E such that for every non-zero subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s : N → E, the fibre product N ×E M ≠ 0.