Derived category
Encyclopedia
In mathematics
, the derived category D(C) of an abelian category
C is a construction of homological algebra
introduced to refine and in a certain sense to simplify the theory of derived functor
s defined on C. The construction proceeds on the basis that the objects of D(C) should be chain complex
es in C, with two such chain complexes considered isomorphic
when there is a chain map that induces an isomorphism on the level of homology
of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hyper-derived functors
. The definitions lead to a significant simplification of formulas otherwise described (not completely faithfully) by complicated spectral sequence
s.
The development of the derived category, by Alexander Grothendieck
and his student Jean-Louis Verdier
shortly after 1960, now appears as one terminal point in the explosive development of homological algebra in the 1950s, a decade in which it had made remarkable strides and became close to appearing as a universal approach to mathematics. The basic theory of Verdier was written down in his dissertation, published finally in 1996 in Astérisque (a summary much earlier appeared in SGA4½
). The axiomatics required an innovation, the concept of triangulated category
, and the construction is based on localization of a category
, a generalisation of localization of a ring
. The original impulse to develop the "derived" formalism came from the need to find a suitable formulation of Grothendieck's coherent duality
theory. Derived categories have since become indispensable also outside of algebraic geometry
, for example in the formulation of the theory of D-module
s and microlocal analysis
.
theory, pushing to the limit of what could be done with Serre duality
without the assumption of a non-singular scheme
, the need to take a whole complex of sheaves in place of a single dualizing sheaf became apparent. In fact the Cohen-Macaulay ring
condition, a weakening of non-singularity, corresponds to the existence of a single dualizing sheaf; and this is far from the general case. From the top-down intellectual position, always assumed by Grothendieck, this signified a need to reformulate. With it came the idea that the 'real' tensor product
and Hom functors would be those existing on the derived level; with respect to those, Tor and Ext become more like computational devices.
Despite the level of abstraction, the derived category methodology established itself over the following decades; and perhaps began to impose itself with the formulation of the Riemann-Hilbert correspondence in dimensions greater than 1 in derived terms, around 1980. The Sato
school adopted it, and the subsequent history of D-module
s was of a theory expressed in those terms.
A parallel development, speaking in fact the same language, was that of spectrum
in homotopy theory. This was at the space level, rather than in the algebra
.
be an abelian category
. We obtain the derived category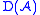
in several steps:
The second step may be bypassed since a homotopy equivalence is in particular a quasi-isomorphism. But then the simple roof definition of morphisms must be relaced by a more complicated one using finite strings of morphisms (technically, it is no longer a calculus of fractions), and the triangulated category
structure of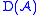
arises in the homotopy category. So the one step construction is more efficient in a way but more complicated and the result is less powerful.
If one adopts the classical point of view on categories, that morphisms have to be sets (not just classes
), then one has to give an additional argument, why this is true. If, for example, the abelian category
is small, i.e. has only a set of objects, then this issue will be no problem.
Composition of morphisms, i.e. roofs, in the derived category is accomplished by finding a third roof on top of the two roofs to be composed. It may be checked that this is possible and gives a well-defined, associative composition.
As the localization of K(A) (which is a triangulated category
), the derived category is triangulated as well. Distinguished triangles are those quasi-isomorphic to triangles of the form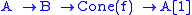
for two complexes A and B and a map f between them. This includes in particular triangles of the form 
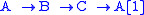for a short exact sequence
in
.
, so the second step in the above construction may be omitted. The definition is usually given in this way because it reveals the existence of a canonical functor
In concrete situations, it is very difficult or impossible to handle morphisms in the derived category directly. Therefore one looks for a more manageable category which is equivalent to the derived category. Classically, there are two (dual) approaches to this: projective and injective resolutions. In both cases, the restriction of the above canonical functor to an appropriate subcategory will be an equivalence of categories
.
In the following we will describe the role of injective resolutions in the context of the derived category, which is the basis for defining right derived functors, which in turn have important applications in cohomology
of sheaves
on topological space
s or more advanced cohomologies like étale cohomology
or group cohomology
.
In order to apply this technique, one has to assume that the abelian category in question has enough injectives which means that every object A of the category admits a monomorphism
to an injective object
I. (Neither the map nor the injective object has to be uniquely specified). This assumption is often satisfied. For example, it is true for the abelian category of R-modules
over a fixed ring
R or for sheaves
of abelian groups on a topological space
.
Embedding A into some injective object I0, the cokernel
of this map into some injective I1 etc., one constructs an injective resolution of A, i.e. an exact
(in general infinite) complex
where the I* are injective objects. This idea generalizes to give resolutions of bounded-below complexes A, i.e. An = 0 for sufficiently small n. As remarked above, injective resolutions are not uniquely defined, but it is a fact that any two resolutions are homotopy equivalent to each other, i.e. isomorphic in the homotopy category. Moreover, morphisms of complexes extend uniquely to a morphism of two given injective resolutions.
This is the point where the homotopy category comes into play again: mapping an object A of
to (any) injective resolution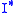 
of A extends to a functor
from the bounded below derived category to the bounded below homotopy category of complexes whose terms are injective objects in
.
It is not difficult to see that this functor is actually inverse to the restriction of the canonical localization functor mentioned in the beginning. In other words, morphisms Hom(A,B) in the derived category may be computed by resolving both A and B and computing the morphisms in the homotopy category, which is at least theoretically easier.
Dually, assuming that
has enough projectives, i.e. for every object A there is a epimorphism
map from a projective object P to A, one can use projective resolutions instead of injective ones.
In addition to these resolution techniques there are similar ones which apply to special cases, and which elegantly avoid the problem with bounded-above or -below restrictions: uses so-called K-injective and K-projective resolutions, and (in a slightly different language) introduced so called cell-modules and semi-free modules, respectively.
More generally, carefully adapting the definitions, it is possible to define the derived category of an exact category
.
be a functor of abelian categories. There are two dual concepts:
In the following we will describe right derived functors. So, assume that F is left exact. Typical examples are
, 
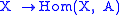or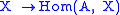 
for some fixed object A, or the global sections functor on sheaves
or the direct image functor
. Their right derived functors are Extn(–,A), Extn(A,–), Hn(X, F)
or Rnf∗ (F), respectively.
The derived category allows to encapsulate all derived functors RnF in one functor, namely the so-called total derived functor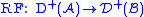
. It is the following composition: 
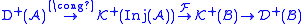, where the first equivalence of categories is described above. The classical derived functors are related to the total one via 
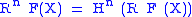. One might say that the RnF forget the chain complex and keep only the cohomologies, whereas R F does keep track of the complexes.
The derived categories is in a sense the "right" place to study these functors. For example, the Grothendieck spectral sequence
of a composition of two functors
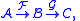
such that F maps injective object
s in A to G-acyclics (i.e. RiG(F(I)) = 0 for all i > 0 and injective I), is an expression of the following identity of total derived functors
J.-L. Verdier showed how derived functors associated with an abelian category A can be viewed as Kan extension
s along embeddings of A into suitable derived categories [Mac Lane].
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the derived category D(C) of an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
C is a construction of homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
introduced to refine and in a certain sense to simplify the theory of derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s defined on C. The construction proceeds on the basis that the objects of D(C) should be chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es in C, with two such chain complexes considered isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
when there is a chain map that induces an isomorphism on the level of homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of the chain complexes. Derived functors can then be defined for chain complexes, refining the concept of hyper-derived functors
Hyperhomology
In homological algebra, the hyperhomology or hypercohomology of a complexof objects of an abelian category is an extension of the usual homology of an object to complexes....
. The definitions lead to a significant simplification of formulas otherwise described (not completely faithfully) by complicated spectral sequence
Spectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
s.
The development of the derived category, by Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
and his student Jean-Louis Verdier
Jean-Louis Verdier
Jean-Louis Verdier was a French mathematician who worked, under the guidance of Alexander Grothendieck, on derived categories and Verdier duality...
shortly after 1960, now appears as one terminal point in the explosive development of homological algebra in the 1950s, a decade in which it had made remarkable strides and became close to appearing as a universal approach to mathematics. The basic theory of Verdier was written down in his dissertation, published finally in 1996 in Astérisque (a summary much earlier appeared in SGA4½
Grothendieck's Séminaire de géométrie algébrique
In mathematics, the Séminaire de Géométrie Algébrique du Bois Marie was an influential seminar run by Alexander Grothendieck. It was a unique phenomenon of research and publication outside of the main mathematical journals that ran from 1960 to 1969 at the IHÉS near Paris...
). The axiomatics required an innovation, the concept of triangulated category
Triangulated category
A triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
, and the construction is based on localization of a category
Localization of a category
In mathematics, localization of a category consists of adding to a category inverse morphisms for some collection of morphisms, constraining them to become isomorphisms. This is formally similar to the process of localization of a ring; it in general makes objects isomorphic that were not so before...
, a generalisation of localization of a ring
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
. The original impulse to develop the "derived" formalism came from the need to find a suitable formulation of Grothendieck's coherent duality
Coherent duality
In mathematics, coherent duality is any of a number of generalisations of Serre duality, applying to coherent sheaves, in algebraic geometry and complex manifold theory, as well as some aspects of commutative algebra that are part of the 'local' theory....
theory. Derived categories have since become indispensable also outside of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, for example in the formulation of the theory of D-module
D-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
s and microlocal analysis
Microlocal analysis
In mathematical analysis, microlocal analysis comprises techniques developed from the 1950s onwards based on Fourier transforms related to the study of variable-coefficients-linear and nonlinear partial differential equations...
.
Motivations
In coherent sheafCoherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
theory, pushing to the limit of what could be done with Serre duality
Serre duality
In algebraic geometry, a branch of mathematics, Serre duality is a duality present on non-singular projective algebraic varieties V of dimension n . It shows that a cohomology group Hi is the dual space of another one, Hn−i...
without the assumption of a non-singular scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
, the need to take a whole complex of sheaves in place of a single dualizing sheaf became apparent. In fact the Cohen-Macaulay ring
Cohen-Macaulay ring
In mathematics, a Cohen–Macaulay ring is a particular type of commutative ring, possessing some of the algebraic-geometric properties of a nonsingular variety, such as local equidimensionality....
condition, a weakening of non-singularity, corresponds to the existence of a single dualizing sheaf; and this is far from the general case. From the top-down intellectual position, always assumed by Grothendieck, this signified a need to reformulate. With it came the idea that the 'real' tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
and Hom functors would be those existing on the derived level; with respect to those, Tor and Ext become more like computational devices.
Despite the level of abstraction, the derived category methodology established itself over the following decades; and perhaps began to impose itself with the formulation of the Riemann-Hilbert correspondence in dimensions greater than 1 in derived terms, around 1980. The Sato
Mikio Sato
is a Japanese mathematician, who started the field of algebraic analysis. He studied at the University of Tokyo, and then did graduate study in physics as a student of Shin'ichiro Tomonaga...
school adopted it, and the subsequent history of D-module
D-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
s was of a theory expressed in those terms.
A parallel development, speaking in fact the same language, was that of spectrum
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
in homotopy theory. This was at the space level, rather than in the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
.
Definition
Let be an abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
. We obtain the derived category
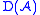in several steps:
- The basic object is the category
of chain complexes in 
. Its objects will be the objects of the derived category but its morphisms will be altered. - Pass to the homotopy category of chain complexesHomotopy category of chain complexesIn homological algebra in mathematics, the homotopy category K of chain complexes in an additive category A is a framework for working with chain homotopies and homotopy equivalences...
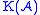by identifying morphisms which are chain homotopic. - Pass to the derived category
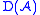by localizingLocalization of a categoryIn mathematics, localization of a category consists of adding to a category inverse morphisms for some collection of morphisms, constraining them to become isomorphisms. This is formally similar to the process of localization of a ring; it in general makes objects isomorphic that were not so before...
at the set of quasi-isomorphismQuasi-isomorphismIn homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
s. Morphisms in the derived category may be explicitly described as roofs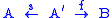
, where s is a quasi-isomorphism and f is any morphism of chain complexes.
The second step may be bypassed since a homotopy equivalence is in particular a quasi-isomorphism. But then the simple roof definition of morphisms must be relaced by a more complicated one using finite strings of morphisms (technically, it is no longer a calculus of fractions), and the triangulated category
Triangulated category
A triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
structure of
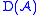arises in the homotopy category. So the one step construction is more efficient in a way but more complicated and the result is less powerful.Remarks
For certain purposes (see below) one uses bounded-below (An=0 for n<<0), bounded-above (An=0 for n>>0) or bounded (An=0 for |n|>>0) complexes instead of unbounded ones. The corresponding derived categories are usually denoted D+(A), D-(A) and Db(A), respectively.If one adopts the classical point of view on categories, that morphisms have to be sets (not just classes
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
), then one has to give an additional argument, why this is true. If, for example, the abelian category
is small, i.e. has only a set of objects, then this issue will be no problem.Composition of morphisms, i.e. roofs, in the derived category is accomplished by finding a third roof on top of the two roofs to be composed. It may be checked that this is possible and gives a well-defined, associative composition.
As the localization of K(A) (which is a triangulated category
Triangulated category
A triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
), the derived category is triangulated as well. Distinguished triangles are those quasi-isomorphic to triangles of the form
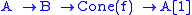for two complexes A and B and a map f between them. This includes in particular triangles of the form 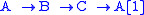for a short exact sequencein
.Projective and injective resolutions
One can easily show that a homotopy equivalence is a quasi-isomorphismQuasi-isomorphism
In homological algebra, a branch of mathematics, a quasi-isomorphism is a morphism A → B of chain complexes such that the induced morphisms...
, so the second step in the above construction may be omitted. The definition is usually given in this way because it reveals the existence of a canonical functor
In concrete situations, it is very difficult or impossible to handle morphisms in the derived category directly. Therefore one looks for a more manageable category which is equivalent to the derived category. Classically, there are two (dual) approaches to this: projective and injective resolutions. In both cases, the restriction of the above canonical functor to an appropriate subcategory will be an equivalence of categories
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
.
In the following we will describe the role of injective resolutions in the context of the derived category, which is the basis for defining right derived functors, which in turn have important applications in cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s or more advanced cohomologies like étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
or group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
.
In order to apply this technique, one has to assume that the abelian category in question has enough injectives which means that every object A of the category admits a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
to an injective object
Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
I. (Neither the map nor the injective object has to be uniquely specified). This assumption is often satisfied. For example, it is true for the abelian category of R-modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a fixed ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R or for sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of abelian groups on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.
Embedding A into some injective object I0, the cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of this map into some injective I1 etc., one constructs an injective resolution of A, i.e. an exact
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
(in general infinite) complex
where the I* are injective objects. This idea generalizes to give resolutions of bounded-below complexes A, i.e. An = 0 for sufficiently small n. As remarked above, injective resolutions are not uniquely defined, but it is a fact that any two resolutions are homotopy equivalent to each other, i.e. isomorphic in the homotopy category. Moreover, morphisms of complexes extend uniquely to a morphism of two given injective resolutions.
This is the point where the homotopy category comes into play again: mapping an object A of
to (any) injective resolution 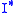of A extends to a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the bounded below derived category to the bounded below homotopy category of complexes whose terms are injective objects in
.It is not difficult to see that this functor is actually inverse to the restriction of the canonical localization functor mentioned in the beginning. In other words, morphisms Hom(A,B) in the derived category may be computed by resolving both A and B and computing the morphisms in the homotopy category, which is at least theoretically easier.
Dually, assuming that
has enough projectives, i.e. for every object A there is a epimorphismEpimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
map from a projective object P to A, one can use projective resolutions instead of injective ones.
In addition to these resolution techniques there are similar ones which apply to special cases, and which elegantly avoid the problem with bounded-above or -below restrictions: uses so-called K-injective and K-projective resolutions, and (in a slightly different language) introduced so called cell-modules and semi-free modules, respectively.
More generally, carefully adapting the definitions, it is possible to define the derived category of an exact category
Exact category
In mathematics, an exact category is a concept of category theory due to Daniel Quillen which is designed to encapsulate the properties of short exact sequences in abelian categories without requiring that morphisms actually possess kernels and cokernels, which is necessary for the usual definition...
.
The relation to derived functors
The derived category is a natural framework to define and study derived functors. In the following, let be a functor of abelian categories. There are two dual concepts:
- right derived functors are "deriving" left exact functors and are calculated via injective resolutions
- left derived functors come from right exact functors and are calculated via projective resolutions
In the following we will describe right derived functors. So, assume that F is left exact. Typical examples are
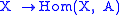, or 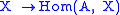for some fixed object A, or the global sections functor on sheavesSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
or the direct image functor
Direct image functor
In mathematics, in the field of sheaf theory and especially in algebraic geometry, the direct image functor generalizes the notion of a section of a sheaf to the relative case.-Definition:...
. Their right derived functors are Extn(–,A), Extn(A,–), Hn(X, F)
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
or Rnf∗ (F), respectively.
The derived category allows to encapsulate all derived functors RnF in one functor, namely the so-called total derived functor
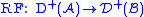. It is the following composition: 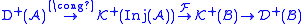, where the first equivalence of categories is described above. The classical derived functors are related to the total one via 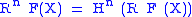. One might say that the RnF forget the chain complex and keep only the cohomologies, whereas R F does keep track of the complexes.The derived categories is in a sense the "right" place to study these functors. For example, the Grothendieck spectral sequence
Grothendieck spectral sequence
In mathematics, in the field of homological algebra, the Grothendieck spectral sequence is a technique that allows one to compute the derived functors of the composition of two functors G\circ F, from knowledge of the derived functors of F and G.If...
of a composition of two functors
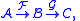
such that F maps injective object
Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
s in A to G-acyclics (i.e. RiG(F(I)) = 0 for all i > 0 and injective I), is an expression of the following identity of total derived functors
- R(G○F) ≅ RG○RF.
J.-L. Verdier showed how derived functors associated with an abelian category A can be viewed as Kan extension
Kan extension
Kan extensions are universal constructs in category theory, a branch of mathematics. They are closely related to adjoints, but are also related to limits and ends. They are named after Daniel M...
s along embeddings of A into suitable derived categories [Mac Lane].