.gif)
Product (category theory)
Encyclopedia
In category theory
, the product of two (or more) objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets
, the direct product of groups
, the direct product of rings and the product of topological spaces
. Essentially, the product of a family of objects is the "most general" object which admits a morphism to each of the given objects.
 be a category with some objects
be a category with some objects 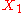 and
and 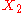 . An object
. An object  is the product of
is the product of 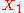 and
and 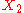 , denoted
, denoted 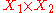 , iff it satisfies this universal property
, iff it satisfies this universal property
:
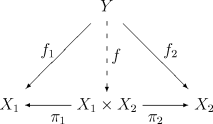 The unique morphism
The unique morphism  is called the product of morphisms
is called the product of morphisms 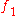 and
and 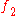 and is denoted
and is denoted 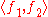 .
.
Above we defined the binary product. Instead of two objects we can take an arbitrary family
of objects indexed by some set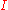 . Then we obtain the definition of a product.
. Then we obtain the definition of a product.
An object is the product of a family
is the product of a family 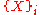 of objects iff there exist morphisms
of objects iff there exist morphisms 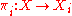 , such that for every object
, such that for every object  and a
and a 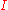 -indexed family of morphisms
-indexed family of morphisms 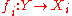 there exists a unique morphism
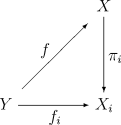
there exists a unique morphism 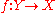 such that the following diagrams commute for all
such that the following diagrams commute for all  :
:
 The product is denoted
The product is denoted 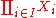 ; if
; if 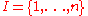 , then denoted
, then denoted  and the product of morphisms is denoted
and the product of morphisms is denoted  .
.
Alternatively, product may be defined totally by equations, here is an example for binary product:
Also product may be derived from limit
. A family of objects is a diagram
without morphisms. If we regard our diagram as a functor, it is a functor from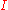 considered as a discrete category
considered as a discrete category
. Then the definition of product coincides with the definition of limit,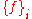 being a cone
being a cone
and projections being the limit (limiting cone).
As well as limit, product may be defined via universal property. For comparison see Limit#Universal property. Lets unfold that definition for binary product. In our case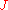 is a discrete category with two objects,
is a discrete category with two objects, 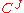 is simply the product category
is simply the product category
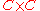 , diagonal functor
, diagonal functor  assigns to each object
assigns to each object  the ordered pair
the ordered pair
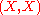 and to each morphism
and to each morphism  the pair
the pair 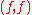 . The product
. The product 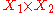 in
in  is given by a universal morphism from the functor
is given by a universal morphism from the functor  to the object
to the object 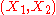 in
in 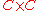 . This universal morphism consists of an object
. This universal morphism consists of an object  of
of  and a morphism
and a morphism 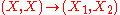 which contains projections.
which contains projections.
with the canonical projections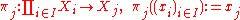
Given any set Y with a family of functions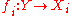
the universal arrow f is defined as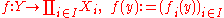
(i.e.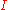 is the empty set
is the empty set
) is the same as a terminal object, and some categories, such as the category of infinite groups, do not have a terminal object: given any infinite group there are infinitely many morphisms
there are infinitely many morphisms  , so
, so  cannot be terminal.
cannot be terminal.
If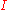 is a set such that all products for families indexed with
is a set such that all products for families indexed with 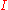 exist, then it is possible to choose the products in a compatible fashion so that the product turns into a functor
exist, then it is possible to choose the products in a compatible fashion so that the product turns into a functor
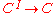 . How this functor maps objects is obvious. Mapping of morphisms is subtle, because product of morphisms defined above does not fit. First, consider binary product functor, which is a bifunctor. For
. How this functor maps objects is obvious. Mapping of morphisms is subtle, because product of morphisms defined above does not fit. First, consider binary product functor, which is a bifunctor. For 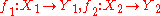 we should find a morphism
we should find a morphism  . We choose
. We choose 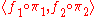 . This operation on morphisms is called cartesian product of morphisms. Second, consider product functor. For families
. This operation on morphisms is called cartesian product of morphisms. Second, consider product functor. For families 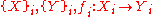 we should find a morphism
we should find a morphism  . We choose the product of morphisms
. We choose the product of morphisms 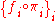 .
.
A category where every finite set of objects has a product is sometimes called a cartesian category
(although some authors use this phrase to mean "a category with all finite limits").
Suppose is a cartesian category, product functors have been chosen as above, and
is a cartesian category, product functors have been chosen as above, and 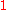 denotes the terminal object of
denotes the terminal object of  . We then have natural isomorphisms
. We then have natural isomorphisms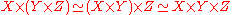
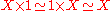

These properties are formally similar to those of a commutative monoid
; a category with its finite products constitutes a symmetric monoidal category
.
. To see this, note that we have various canonical projections and injections which fill out the diagram
The universal property for X×(Y+Z) then guarantees a unique morphism X×Y+X×Z → X×(Y+Z). A distributive category
is one in which this morphism is actually an isomorphism. Thus in a distributive category, one has the canonical isomorphism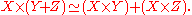
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the product of two (or more) objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, the direct product of groups
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
, the direct product of rings and the product of topological spaces
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
. Essentially, the product of a family of objects is the "most general" object which admits a morphism to each of the given objects.
Definition
Let be a category with some objects
be a category with some objects 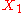 and
and 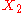 . An object
. An object  is the product of
is the product of 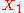 and
and 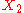 , denoted
, denoted 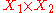 , iff it satisfies this universal property
, iff it satisfies this universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
:
- there exist morphisms
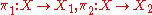 , called the canonical projections or projection morphisms, such that for every object
, called the canonical projections or projection morphisms, such that for every object  and pair of morphisms
and pair of morphisms 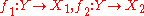 there exists a unique morphism
there exists a unique morphism 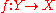 such that the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
such that the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:

 is called the product of morphisms
is called the product of morphisms 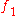 and
and 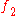 and is denoted
and is denoted 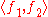 .
.Above we defined the binary product. Instead of two objects we can take an arbitrary family
Indexed family
In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of objects indexed by some set
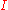 . Then we obtain the definition of a product.
. Then we obtain the definition of a product.An object
 is the product of a family
is the product of a family 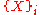 of objects iff there exist morphisms
of objects iff there exist morphisms 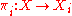 , such that for every object
, such that for every object  and a
and a 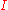 -indexed family of morphisms
-indexed family of morphisms 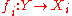 there exists a unique morphism
there exists a unique morphism 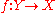 such that the following diagrams commute for all
such that the following diagrams commute for all  :
:
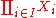 ; if
; if 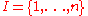 , then denoted
, then denoted  and the product of morphisms is denoted
and the product of morphisms is denoted  .
.Alternatively, product may be defined totally by equations, here is an example for binary product:
- Existence of
 is guaranteed by the operation
is guaranteed by the operation 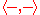 .
. - Commutativity of diagrams above are guaranteed by the equality
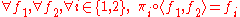 .
. - Uniqueness of
 is guaranteed by the equality
is guaranteed by the equality 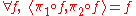 .
.
Also product may be derived from limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
. A family of objects is a diagram
Diagram (category theory)
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
without morphisms. If we regard our diagram as a functor, it is a functor from
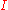 considered as a discrete category
considered as a discrete categoryDiscrete category
In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
. Then the definition of product coincides with the definition of limit,
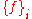 being a cone
being a coneCone (category theory)
In category theory, a branch of mathematics, the cone of a functor is an abstract notion used to define the limit of that functor. Cones make other appearances in category theory as well.-Definition:...
and projections being the limit (limiting cone).
As well as limit, product may be defined via universal property. For comparison see Limit#Universal property. Lets unfold that definition for binary product. In our case
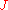 is a discrete category with two objects,
is a discrete category with two objects, 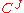 is simply the product category
is simply the product categoryProduct category
In the mathematical field of category theory, the product of two categories C and D, denoted and called a product category, is a straightforward extension of the concept of the Cartesian product of two sets.-Definition:...
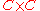 , diagonal functor
, diagonal functor  assigns to each object
assigns to each object  the ordered pair
the ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
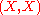 and to each morphism
and to each morphism  the pair
the pair 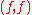 . The product
. The product 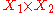 in
in  is given by a universal morphism from the functor
is given by a universal morphism from the functor  to the object
to the object 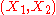 in
in 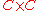 . This universal morphism consists of an object
. This universal morphism consists of an object  of
of  and a morphism
and a morphism 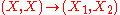 which contains projections.
which contains projections.Examples
- In the category Set (the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
), the product in the category theoretic sense is the cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
. Given a family of sets Xi the product is defined as
with the canonical projections
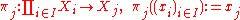
Given any set Y with a family of functions
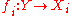
the universal arrow f is defined as
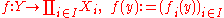
- In the category of topological spacesCategory of topological spacesIn mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, the product is the space whose underlying set is the cartesian product and which carries the product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
.
- In the category of modules over some ring R, the product is the cartesian product with addition defined componentwise and distributive multiplication.
- In the category of groupsCategory of groupsIn mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, the product is given by the cartesian product with multiplication defined componentwise.
- In the category of algebraic varietiesAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, the categorical product is given by the Segre embeddingSegre embeddingIn mathematics, the Segre embedding is used in projective geometry to consider the cartesian product of two or more projective spaces as a projective variety...
.
- In the category of semi-abelian monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s, the categorical product is given by the history monoidHistory monoidIn mathematics and computer science, a history monoid is a way of representing the histories of concurrently running computer processes as a collection of strings, each string representing the individual history of a process...
.
- A partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
can be treated as a category, using the order relation as the morphisms. In this case the products and coproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s correspond to greatest lower bounds (meetsMeet (mathematics)In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
) and least upper bounds (joins).
Discussion
The product does not necessarily exist. For example, an empty productEmpty product
In mathematics, an empty product, or nullary product, is the result of multiplying no factors. It is equal to the multiplicative identity 1, given that it exists for the multiplication operation in question, just as the empty sum—the result of adding no numbers—is zero, or the additive...
(i.e.
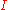 is the empty set
is the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
) is the same as a terminal object, and some categories, such as the category of infinite groups, do not have a terminal object: given any infinite group
 there are infinitely many morphisms
there are infinitely many morphisms  , so
, so  cannot be terminal.
cannot be terminal.If
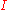 is a set such that all products for families indexed with
is a set such that all products for families indexed with 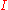 exist, then it is possible to choose the products in a compatible fashion so that the product turns into a functor
exist, then it is possible to choose the products in a compatible fashion so that the product turns into a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
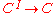 . How this functor maps objects is obvious. Mapping of morphisms is subtle, because product of morphisms defined above does not fit. First, consider binary product functor, which is a bifunctor. For
. How this functor maps objects is obvious. Mapping of morphisms is subtle, because product of morphisms defined above does not fit. First, consider binary product functor, which is a bifunctor. For 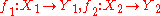 we should find a morphism
we should find a morphism  . We choose
. We choose 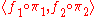 . This operation on morphisms is called cartesian product of morphisms. Second, consider product functor. For families
. This operation on morphisms is called cartesian product of morphisms. Second, consider product functor. For families 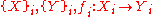 we should find a morphism
we should find a morphism  . We choose the product of morphisms
. We choose the product of morphisms 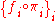 .
.A category where every finite set of objects has a product is sometimes called a cartesian category
(although some authors use this phrase to mean "a category with all finite limits").
Suppose
 is a cartesian category, product functors have been chosen as above, and
is a cartesian category, product functors have been chosen as above, and 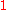 denotes the terminal object of
denotes the terminal object of  . We then have natural isomorphisms
. We then have natural isomorphisms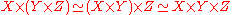
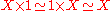

These properties are formally similar to those of a commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
; a category with its finite products constitutes a symmetric monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
.
Distributivity
In a category with finite products and coproducts, there is a canonical morphism X×Y+X×Z → X×(Y+Z), where the plus sign here denotes the coproductCoproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
. To see this, note that we have various canonical projections and injections which fill out the diagram
The universal property for X×(Y+Z) then guarantees a unique morphism X×Y+X×Z → X×(Y+Z). A distributive category
Distributive category
In mathematics, a category is distributive if it has finite products and finite coproducts such that for every choice of objects A,B,C, the canonical map...
is one in which this morphism is actually an isomorphism. Thus in a distributive category, one has the canonical isomorphism
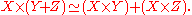
See also
- CoproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
– the dualDual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of the product - Limit and colimitsLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
- Equalizer
- Inverse limitInverse limitIn mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
- Cartesian closed categoryCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
- Categorical pullback
External links
- Interactive Web page which generates examples of products in the category of finite sets. Written by Jocelyn Paine.

