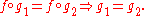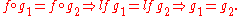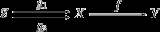
Monomorphism
Encyclopedia
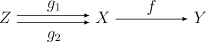
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
or universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, a monomorphism is an injective
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
. A monomorphism from X to Y is often denoted with the notation
 .
.In the more general setting of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a monomorphism (also called a monic morphism or a mono) is a left-cancellative morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
, that is, an arrow such that, for all morphisms ,
Monomorphisms are a categorical generalization of injective function
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
s; in some categories the notions coincide, but monomorphisms are more general, as in the examples below.
The categorical dual of a monomorphism is an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, i.e. a monomorphism in a category C is an epimorphism in the dual category Cop. Every section
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
is a monomorphism, and every retraction is an epimorphism.
Terminology
The companion terms monomorphism and epimorphism were originally introduced by Nicolas BourbakiNicolas Bourbaki
Nicolas Bourbaki is the collective pseudonym under which a group of 20th-century mathematicians wrote a series of books presenting an exposition of modern advanced mathematics, beginning in 1935. With the goal of founding all of mathematics on set theory, the group strove for rigour and generality...
; Bourbaki uses monomorphism as shorthand for an injective function. Early category theorists believed that the correct generalization of injectivity to the context of categories was the cancellation property given above. While this is not exactly true for monic maps, it is very close, so this has caused little trouble, unlike the case of epimorphisms. Saunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
attempted to make a distinction between what he called monomorphisms, which were maps in a concrete category whose underlying maps of sets were injective, and monic maps, which are monomorphisms in the categorical sense of the word. This distinction never came into general use.
Another name for monomorphism is extension, although this has other uses too.
Relation to invertibility
Left invertible maps are necessarily monic: if l is a left inverse for f (meaning ), then f is monic, as
), then f is monic, as
A left invertible map is called a split mono
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
.
A map f : X → Y is monic if and only if the induced map f∗ : Hom(Z, X) → Hom(Z, Y), defined by
 for all morphisms h : Z → X , is injective for all Z.
for all morphisms h : Z → X , is injective for all Z.Examples
Every morphism in a concrete categoryConcrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
whose underlying function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is injective is a monomorphism. In the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, the converse also holds so the monomorphisms are exactly the injective morphisms. The converse also holds in most naturally occurring categories of algebras because of the existence of a free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
on one generator. In particular, it is true in the categories of groups and rings, and in any abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.
It is not true in general, however, that all monomorphisms must be injective in other categories. For example, in the category Div of divisible
Divisible group
In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s and group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s between them there are monomorphisms that are not injective: consider the quotient map q : Q → Q/Z. This is clearly not an injective map; nevertheless, it is a monomorphism in this category. To see this, note that if q ∘ f = q ∘ g for some morphisms f,g : G → Q where G is some divisible abelian group then q ∘ h = 0 where h = f − g (this makes sense as this is an additive category
Additive category
In mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
). This implies that h(x) is an integer if x ∈ G. If h(x) is not 0 then, for instance,
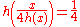
so that
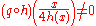 ,
,contradicting q ∘ h = 0, so h(x) = 0 and q is therefore a monomorphism.
Properties
- In a toposToposIn mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
, every monic is an equalizer, and any map that is both monic and epi is an isomorphism. - Every isomorphism is monic.