
Quasi-Frobenius ring
Encyclopedia
In ring theory
, the class of Frobenius rings and their generalizations are the extension of work done on Frobenius algebra
s. Perhaps the most important generalization is that of quasi-Frobenius rings (QF rings), which are in turn generalized by right pseudo-Frobenius rings (PF rings) and right finitely pseudo-Frobenius rings (FPF rings). Other diverse generalizations of quasi-Frobenius rings include QF-1, QF-2 and QF-3 rings.
These types of rings can be viewed as descendants of algebras examined by Georg Frobenius. A partial list of pioneers in quasi-Frobenius rings includes R. Brauer
, K. Morita
, T. Nakayama
, J. Nesbitt
, and R.M. Thrall.
A ring R is quasi-Frobenius if and only if R satisfies any of the following equivalent conditions:
A Frobenius ring R is one satisfying any of the following equivalent conditions. Let J=J(R) be the Jacobson radical
of R.
For a commutative ring R, the following are equivalent:
A ring R is right pseudo-Frobenius if any of the following equivalent conditions are met:
A ring R is right finitely pseudo-Frobenius if and only if every finitely generated
faithful right R module is a generator of Mod-R.
and H. Tachikawa.
Following , let R be a left or right Artinian ring:
(In other words, R = End(M) = End(N). In general, it is possible for an endomorphism ring to strictly contain R.)
The numbering scheme does not necessarily outline a hierarchy. Under more lax conditions, these three classes of rings may not contain each other. Under the assumption that R is left or right Artinian however, QF-2 rings are QF-3. There is even an example of a QF-1 and QF-3 ring which is not QF-2.
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, the class of Frobenius rings and their generalizations are the extension of work done on Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
s. Perhaps the most important generalization is that of quasi-Frobenius rings (QF rings), which are in turn generalized by right pseudo-Frobenius rings (PF rings) and right finitely pseudo-Frobenius rings (FPF rings). Other diverse generalizations of quasi-Frobenius rings include QF-1, QF-2 and QF-3 rings.
These types of rings can be viewed as descendants of algebras examined by Georg Frobenius. A partial list of pioneers in quasi-Frobenius rings includes R. Brauer
Richard Brauer
Richard Dagobert Brauer was a leading German and American mathematician. He worked mainly in abstract algebra, but made important contributions to number theory...
, K. Morita
Kiiti Morita
was a Japanese mathematician working in algebra and topology.He received his Ph.D. from the University of Osaka in 1950 and was professor at the University of Tsukuba....
, T. Nakayama
Tadashi Nakayama (mathematician)
was a mathematician who made important contributions to representation theory. He received his degrees from Tokyo University and Osaka University and held permanent positions at Osaka University and Nagoya University. He had visiting positions at Princeton University, Illinois University, and...
, J. Nesbitt
Cecil J. Nesbitt
Cecil James Nesbitt, Ph.D., F.S.A., M.A.A.A. was a mathematician who was a Ph.D. student of Richard Brauer and wrote many influential papers in the early history of modular representation theory. He taught actuarial mathematics at the University of Michigan from 1938 to 1980. Nesbitt was born in...
, and R.M. Thrall.
Definitions
For the sake of presentation, it will be easier to define quasi-Frobenius rings first. In the following characterizations of each type of ring, many properties of the ring will be revealed.A ring R is quasi-Frobenius if and only if R satisfies any of the following equivalent conditions:
- R is NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
on one side and self-injective on one side. - R is ArtinianArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
on a side and self-injective on a side. - All right (or all left) R modules which are projectiveProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
are also injectiveInjective moduleIn mathematics, especially in the area of abstract algebra known as module theory, an injective module is a module Q that shares certain desirable properties with the Z-module Q of all rational numbers...
. - All right (or all left) R modules which are injective are also projective.
A Frobenius ring R is one satisfying any of the following equivalent conditions. Let J=J(R) be the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of R.
- R is quasi-Frobenius and the socleSocleSocle may refer to:* Socle * Socle...
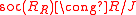 as right R modules.
as right R modules. - R is quasi-Frobenius and
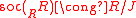 as left R modules.
as left R modules. - As right R modules
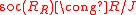 , and as left R modules
, and as left R modules 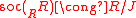 .
.
For a commutative ring R, the following are equivalent:
- R is Frobenius
- R is QF
- R is a finite direct sum of localLocal ringIn abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
artinian rings with simpleSimple moduleIn mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
socles. (Such rings are examples of "zero-dimensional Gorenstein local ringsGorenstein ringIn commutative algebra, a Gorenstein local ring is a Noetherian commutative local ring R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition....
".)
A ring R is right pseudo-Frobenius if any of the following equivalent conditions are met:
- Every faithful right R module is a generatorGenerator (category theory)In category theory in mathematics a generator of a category \mathcal C is an object G of the category, such that for any two different morphisms f, g: X \rightarrow Y in \mathcal C, there is a morphism h : G \rightarrow X, such that the compositions f \circ h \neq g \circ h.Generators are central...
for the category of right R modules. - R is right self-injective and is a cogenerator of Mod-R.
- R is right self-injective and is finitely cogenerated as a right R module.
- R is right self-injective and a right Kasch ring.
- R is right self-injective, semilocal and the socleSocleSocle may refer to:* Socle * Socle...
soc(RR) is an essential submodule of R. - R is a cogenerator of Mod-R and is a left Kasch ring.
A ring R is right finitely pseudo-Frobenius if and only if every finitely generated
Finitely generated
In mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
faithful right R module is a generator of Mod-R.
Thrall's QF-1,2,3 generalizations
In the seminal article , R. M. Thrall focused on three specific properties of (finite dimensional) QF algebras and studied them in isolation. With additional assumptions, these definitions can also be used to generalize QF rings. A few other mathematicians pioneering these generalizations included K. MoritaKiiti Morita
was a Japanese mathematician working in algebra and topology.He received his Ph.D. from the University of Osaka in 1950 and was professor at the University of Tsukuba....
and H. Tachikawa.
Following , let R be a left or right Artinian ring:
- R is QF-1 if for every faithful left R module M and faithful right R module N satisfy the following conditions on endomorphisms:
- If
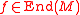 , then for all x in M,
, then for all x in M,  for some r in R.
for some r in R. - If
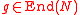 , then for all x in N,
, then for all x in N,  for some r in R.
for some r in R.
- If
(In other words, R = End(M) = End(N). In general, it is possible for an endomorphism ring to strictly contain R.)
- R is QF-2 if each indecomposable projective right module and each indecomposable projective left module has a unique minimal submodule. (I.e. they have simple socles.)
- R is QF-3 if the injective hullInjective hullIn mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
s E(RR) and E(RR) are both projective modules.
The numbering scheme does not necessarily outline a hierarchy. Under more lax conditions, these three classes of rings may not contain each other. Under the assumption that R is left or right Artinian however, QF-2 rings are QF-3. There is even an example of a QF-1 and QF-3 ring which is not QF-2.
Examples
- Every Frobenius k algebra is a Frobenius ring.
- Every semisimple ring is clearly quasi-Frobenius, since all modules are projective and injective. Even more is true however: semisimple rings are all Frobenius. This is easily verified by the definition, since for semisimple rings
 and J = rad(R) = 0.
and J = rad(R) = 0. - The quotient ringQuotient ringIn ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
 is QF for any positive integer n>1.
is QF for any positive integer n>1. - Commutative Artinian serial ringsSerial moduleIn abstract algebra, a uniserial module M is a module over a ring R, whose submodules are totally ordered by inclusion. This means simply that for any two submodules N1 and N2 of M, either N_1\subseteq N_2 or N_2\subseteq N_1. A module is called a serial module if it is a direct sum of uniserial...
are all Frobenius, and in fact have the additional property that every quotient ring R/I is also Frobenius. It turns out that among commutative Artinian rings, the serial rings are exactly the rings whose (nonzero) quotients are all Frobenius. - Many exotic PF and FPF rings can be found as examples in

