Transfer operator
Encyclopedia
In mathematics
, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics
, quantum chaos
and fractals. The transfer operator is sometimes called the Ruelle operator, after David Ruelle
, or the Ruelle–Perron–Frobenius operator in reference to the applicability of the Frobenius–Perron theorem to the determination of the eigenvalues of the operator.
The iterated function to be studied is a map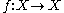
for an arbitrary set 
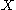. The transfer operator is defined as an operator 
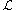acting on the space of functions 
as
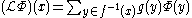
where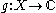
is an auxiliary valuation function. When 
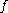has a Jacobian determinant, then 
is usually taken to be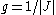 
.
The above definition of the transfer operator can be shown to be the point-set limit of the measure-theoretic pushforward
of g: in essence, the transfer operator is the direct image functor
in the category of measurable spaces. The left-adjoint of the Frobenius–Perron operator is the Koopman operator or composition operator
.
naturally leads to a study of the orbits of points of X under iteration (the study of point dynamics
), the transfer operator defines how (smooth) maps evolve under iteration. Thus, transfer operators typically appear in physics
problems, such as quantum chaos
and statistical mechanics
, where attention is focused on the time evolution of smooth functions.
It is often the case that the transfer operator is positive, has discrete positive real-valued eigenvalues, with the largest eigenvalue being equal to one. For this reason, the transfer operator is sometimes called the Frobenius–Perron operator.
The eigenfunction
s of the transfer operator are usually fractals. When the logarithm of the transfer operator corresponds to a quantum Hamiltonian, the eigenvalues will typically be very closely spaced, and thus even a very narrow and carefully selected ensemble of quantum states will encompass a large number of very different fractal eigenstates with non-zero support
over the entire volume. This can be used to explain many results from classical statistical mechanics, including the irreversibility of time and the increase of entropy
.
The transfer operator of the Bernoulli map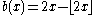
is exactly solvable and is a classic example of deterministic chaos
; the discrete eigenvalues correspond to the Bernoulli polynomials
. This operator also has a continuous spectrum consisting of the Hurwitz zeta function.
The transfer operator of the Gauss map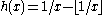
is called the Gauss–Kuzmin–Wirsing (GKW) operator and due to its extraordinary difficulty, has not been fully solved. The theory of the GKW dates back to a hypothesis by Gauss on continued fraction
s and is closely related to the Riemann zeta function.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, quantum chaos
Quantum chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
and fractals. The transfer operator is sometimes called the Ruelle operator, after David Ruelle
David Ruelle
David Pierre Ruelle is a Belgian-French mathematical physicist. He has worked on statistical physics and dynamical systems. With Floris Takens he coined the term strange attractor, and founded a new theory of turbulence...
, or the Ruelle–Perron–Frobenius operator in reference to the applicability of the Frobenius–Perron theorem to the determination of the eigenvalues of the operator.
The iterated function to be studied is a map
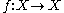for an arbitrary set 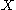. The transfer operator is defined as an operator 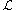acting on the space of functions as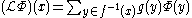where
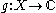is an auxiliary valuation function. When 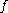has a Jacobian determinant, then is usually taken to be 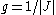.The above definition of the transfer operator can be shown to be the point-set limit of the measure-theoretic pushforward
Pushforward
The notion of pushforward in mathematics is "dual" to the notion of pullback, and can mean a number of different, but closely related things.*Pushforward : the differential of a smooth map between manifolds, and the "pushforward" operations it defines.**Pushforward #Pushforward of vector...
of g: in essence, the transfer operator is the direct image functor
Direct image functor
In mathematics, in the field of sheaf theory and especially in algebraic geometry, the direct image functor generalizes the notion of a section of a sheaf to the relative case.-Definition:...
in the category of measurable spaces. The left-adjoint of the Frobenius–Perron operator is the Koopman operator or composition operator
Composition operator
In mathematics, the composition operator C_\phi with symbol \phi is a linear operator defined by the ruleC_\phi = f \circ\phiwhere f \circ\phi denotes function composition. In physics, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman...
.
Applications
Whereas the iteration of a function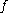 naturally leads to a study of the orbits of points of X under iteration (the study of point dynamicsChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
), the transfer operator defines how (smooth) maps evolve under iteration. Thus, transfer operators typically appear in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
problems, such as quantum chaos
Quantum chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, where attention is focused on the time evolution of smooth functions.
It is often the case that the transfer operator is positive, has discrete positive real-valued eigenvalues, with the largest eigenvalue being equal to one. For this reason, the transfer operator is sometimes called the Frobenius–Perron operator.
The eigenfunction
Eigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s of the transfer operator are usually fractals. When the logarithm of the transfer operator corresponds to a quantum Hamiltonian, the eigenvalues will typically be very closely spaced, and thus even a very narrow and carefully selected ensemble of quantum states will encompass a large number of very different fractal eigenstates with non-zero support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
over the entire volume. This can be used to explain many results from classical statistical mechanics, including the irreversibility of time and the increase of entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
.
The transfer operator of the Bernoulli map
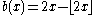is exactly solvable and is a classic example of deterministic chaosChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
; the discrete eigenvalues correspond to the Bernoulli polynomials
Bernoulli polynomials
In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
. This operator also has a continuous spectrum consisting of the Hurwitz zeta function.
The transfer operator of the Gauss map
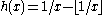is called the Gauss–Kuzmin–Wirsing (GKW) operator and due to its extraordinary difficulty, has not been fully solved. The theory of the GKW dates back to a hypothesis by Gauss on continued fractionContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s and is closely related to the Riemann zeta function.