
Dynamical outer billiards
Encyclopedia
Outer Billiards is a dynamical system
based on a convex
shape in the plane.
Classically, this system is defined for the Euclidean plane but one can
also consider the system in the hyperbolic plane
or in other spaces that
suitably generalize the plane.
Outer billiards differs from a usual dynamical billiard
in that it deals with a discrete sequence of moves outside the shape rather than inside of it.
shape in the plane.
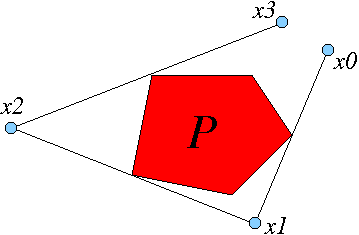
Given a point x0 outside P, there is typically a unique
point x1 (also outside P) so that the line segment connecting x0 to x1 is tangent
to P at its midpoint
and
a person walking from x0 to x1 would see P on the right. (See Figure.) The map
F: x0 -> x1 is called the outer billiards map.
 The inverse
The inverse
(or backwards) outer billiards map is also defined, as the map x1 -> x0.
One gets the inverse map simply by replacing the word right by the word left in the definition given above.
The figure shows the situation in the Euclidean plane, but the definition in the
hyperbolic plane
is essentially the same.
is the set of all iterations
of the point, namely ... x0 <--> x1 <--> x2 <--> x3 ... That is, start at x0 and
iteratively apply both the outer billiards map and the backwards outer billiards map.
When P is a strictly convex shape, such as an ellipse
,
every point in the exterior of P has a well defined orbit. When P
is a polygon
, some points might not have well-defined orbits, on account of the
potential ambiguity of choosing the midpoint of the relevant tangent line. Nevertheless, in
the polygonal case, almost every point has a well-defined orbit.
the scope of this article.
Unlike the case of ordinary billiards
, the definition
is not straightforward. One natural setting for the map is a
complex vector space
. In this case, there is a natural choice of line
tangent to a convex
body at each point. One obtains these tangents
by starting with the normals and using the
complex structure to rotate 90 degrees.
These distinguished tangent lines can be used
to define the outer billiards map roughly as above.
See S. Tabachnikov's book (cited in the references)
for details.
in the late 1950s,
though it seems
that a few people cite an earlier construction in 1945, due to M. Day. Jurgen Moser
popularized the system in the 1970s as a toy model for
celestial mechanics
. This system has been studied classically in the Euclidean plane, and more recently in
the hyperbolic plane
. One can also consider higher dimensional spaces, though no serious study has yet been made.
Bernhard Neumann
informally posed the question as to whether or not one can
have unbounded orbits in an outer billiards system, and Moser put it in writing in 1973.
Sometimes this basic question has been called the Moser-Neumann question.
This question, originally posed for shapes in the Euclidean plane and
solved only recently, has been a
guiding problem in the field.
sketched a proof, based on K.A.M. theory, that outer
billiards relative to a
6-times-differentiable shape of positive curvature has all orbits bounded.
In 1982, R. Douady gave the full proof of this result.
A big advance in the polygonal case came over a period of several years when
three teams of authors, Vivaldi-Shaidenko (1987) , Kolodziej (1989), and Gutkin-Simanyi (1991), each
using different methods,
showed that outer
billiards relative to a quasirational polygon has all orbits bounded. The notion of quasirational is technical
(see references) but it includes the class of regular polygons and convex rational polygons,
namely those convex polygon
s whose vertices have rational
coordinates. In the case of rational polygons, all the orbits are
periodic. In 1995, Tabachnikov showed that outer billiards for the regular pentagon has some aperiodic orbits,
thus clarifying the distinction between the dynamics in the rational and regular cases.
In 1996, Boyland showed that outer billiards relative to some shapes can have orbits which accumulate on
the shape.
In 2005, D. Genin showed that all orbits are bounded when the table is a trapezoid
, thus
showing that quasirationality is not a necessary condition for the system to have all orbits bounded.
(Not all trapezoids are quasirational.)
relative to the Penrose
Kite, thus answering the original Moser-Neumann question in the affirmative.
The Penrose kite is the convex
quadrilateral
from the kites-and-darts Penrose tilings.
Subsequently, Schwartz showed that outer billiards has unbounded orbits when defined relative
to any irrational kite. An
irrational kite is a quadrilateral
with the following property:
One of the diagonals of the quadrilateral
divides the region into two triangles of equal area
and the other diagonal
divides the region into two triangles whose areas are not rational
multiples
of each other.
In 2008, Dolgopyat-Fayad showed that outer billiards defined relative to the semidisk has
unbounded orbits. The semidisk is the region one gets by cutting a disk
in half.
The proof of Dolgopyat-Fayad is robust, and also works for regions obtained by
cutting a disk nearly in half, when the word nearly is suitably interpreted.
for a certain class of convex polygon
s in the hyperbolic plane
.
The authors call such polygons large.
(See the reference for the definition.)
, the existence of periodic
orbits is a major unsolved problem. For instance, it is unknown if every
triangular shaped table has a periodic billiard path. More progress has
been made for outer billiards, though the situation is far from well-understood.
As mentioned above, all the orbits are periodic when the system is defined
relative to a convex rational polygon in the Euclidean plane. Moreover, it is a
recent theorem of C. Culter (written up by S. Tabachnikov) that outer
billiards relative to any convex polygon
has periodic orbits—in fact a
periodic orbit outside of any given bounded region.
Here are some open problems in the area.
only cases known.
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
based on a convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
shape in the plane.
Classically, this system is defined for the Euclidean plane but one can
also consider the system in the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
or in other spaces that
suitably generalize the plane.
Outer billiards differs from a usual dynamical billiard
Dynamical billiards
A billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
in that it deals with a discrete sequence of moves outside the shape rather than inside of it.
The Outer Billiards Map
Let P be a convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
shape in the plane.
Given a point x0 outside P, there is typically a unique
point x1 (also outside P) so that the line segment connecting x0 to x1 is tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to P at its midpoint
Midpoint
The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
and
a person walking from x0 to x1 would see P on the right. (See Figure.) The map
F: x0 -> x1 is called the outer billiards map.

Inverse (mathematics)
In many contexts in mathematics the term inverse indicates the opposite of something. This word and its derivatives are used widely in mathematics, as illustrated below....
(or backwards) outer billiards map is also defined, as the map x1 -> x0.
One gets the inverse map simply by replacing the word right by the word left in the definition given above.
The figure shows the situation in the Euclidean plane, but the definition in the
hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
is essentially the same.
orbits
An outer billiards orbitOrbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
is the set of all iterations
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of the point, namely ... x0 <--> x1 <--> x2 <--> x3 ... That is, start at x0 and
iteratively apply both the outer billiards map and the backwards outer billiards map.
When P is a strictly convex shape, such as an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
,
every point in the exterior of P has a well defined orbit. When P
is a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
, some points might not have well-defined orbits, on account of the
potential ambiguity of choosing the midpoint of the relevant tangent line. Nevertheless, in
the polygonal case, almost every point has a well-defined orbit.
- An orbit is called periodic if it eventually repeats.
- An orbit is called aperiodic (or non-periodic) if it is not periodic.
- An orbit is called bounded (or stable) if some bounded region in the plane contains the whole orbit.
- An orbit is called unbounded (or unstable) if it is not bounded.
higher dimensional spaces
Defining an outer billiards system in a higher dimensional space is beyondthe scope of this article.
Unlike the case of ordinary billiards
Dynamical billiards
A billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
, the definition
is not straightforward. One natural setting for the map is a
complex vector space
Complex vector space
A complex vector space is a vector space over the complex numbers. It can also refer to:* a vector space over the real numbers with a linear complex structure...
. In this case, there is a natural choice of line
tangent to a convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
body at each point. One obtains these tangents
by starting with the normals and using the
complex structure to rotate 90 degrees.
These distinguished tangent lines can be used
to define the outer billiards map roughly as above.
See S. Tabachnikov's book (cited in the references)
for details.
History
Most people attribute the introduction of outer billiards to Bernhard NeumannBernhard Neumann
Bernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
in the late 1950s,
though it seems
that a few people cite an earlier construction in 1945, due to M. Day. Jurgen Moser
Jürgen Moser
Jürgen Kurt Moser or Juergen Kurt Moser was a German-American mathematician.-Professional biography:...
popularized the system in the 1970s as a toy model for
celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
. This system has been studied classically in the Euclidean plane, and more recently in
the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. One can also consider higher dimensional spaces, though no serious study has yet been made.
Bernhard Neumann
Bernhard Neumann
Bernhard Hermann Neumann AC FRS was a German-born British mathematician who was one of the leading figures in group theory, greatly influencing the direction of the subject....
informally posed the question as to whether or not one can
have unbounded orbits in an outer billiards system, and Moser put it in writing in 1973.
Sometimes this basic question has been called the Moser-Neumann question.
This question, originally posed for shapes in the Euclidean plane and
solved only recently, has been a
guiding problem in the field.
bounded orbits in the Euclidean plane
In the 70's, Jurgen MoserJürgen Moser
Jürgen Kurt Moser or Juergen Kurt Moser was a German-American mathematician.-Professional biography:...
sketched a proof, based on K.A.M. theory, that outer
billiards relative to a
6-times-differentiable shape of positive curvature has all orbits bounded.
In 1982, R. Douady gave the full proof of this result.
A big advance in the polygonal case came over a period of several years when
three teams of authors, Vivaldi-Shaidenko (1987) , Kolodziej (1989), and Gutkin-Simanyi (1991), each
using different methods,
showed that outer
billiards relative to a quasirational polygon has all orbits bounded. The notion of quasirational is technical
(see references) but it includes the class of regular polygons and convex rational polygons,
namely those convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
s whose vertices have rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
coordinates. In the case of rational polygons, all the orbits are
periodic. In 1995, Tabachnikov showed that outer billiards for the regular pentagon has some aperiodic orbits,
thus clarifying the distinction between the dynamics in the rational and regular cases.
In 1996, Boyland showed that outer billiards relative to some shapes can have orbits which accumulate on
the shape.
In 2005, D. Genin showed that all orbits are bounded when the table is a trapezoid
Trapezoid
In Euclidean geometry, a convex quadrilateral with one pair of parallel sides is referred to as a trapezoid in American English and as a trapezium in English outside North America. A trapezoid with vertices ABCD is denoted...
, thus
showing that quasirationality is not a necessary condition for the system to have all orbits bounded.
(Not all trapezoids are quasirational.)
unbounded orbits in the Euclidean plane
In 2007, R. E. Schwartz showed that outer billiards has some unbounded orbits when definedrelative to the Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
Kite, thus answering the original Moser-Neumann question in the affirmative.
The Penrose kite is the convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
from the kites-and-darts Penrose tilings.
Subsequently, Schwartz showed that outer billiards has unbounded orbits when defined relative
to any irrational kite. An
irrational kite is a quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
with the following property:
One of the diagonals of the quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
divides the region into two triangles of equal area
and the other diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
divides the region into two triangles whose areas are not rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
multiples
of each other.
In 2008, Dolgopyat-Fayad showed that outer billiards defined relative to the semidisk has
unbounded orbits. The semidisk is the region one gets by cutting a disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
in half.
The proof of Dolgopyat-Fayad is robust, and also works for regions obtained by
cutting a disk nearly in half, when the word nearly is suitably interpreted.
unbounded orbits in the hyperbolic plane
In 2003, Dogru and Tabachnikov showed that all orbits are unboundedfor a certain class of convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
s in the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
.
The authors call such polygons large.
(See the reference for the definition.)
Existence of Periodic Orbits
In ordinary polygonal billiardsDynamical billiards
A billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
, the existence of periodic
orbits is a major unsolved problem. For instance, it is unknown if every
triangular shaped table has a periodic billiard path. More progress has
been made for outer billiards, though the situation is far from well-understood.
As mentioned above, all the orbits are periodic when the system is defined
relative to a convex rational polygon in the Euclidean plane. Moreover, it is a
recent theorem of C. Culter (written up by S. Tabachnikov) that outer
billiards relative to any convex polygon
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
has periodic orbits—in fact a
periodic orbit outside of any given bounded region.
Open Questions
Outer billiards is a subject still in its beginning phase. Most problems are still unsolved.Here are some open problems in the area.
- Show that outer billiards relative to almost every convex polygonConvex polygonIn geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
has unbounded orbits.
- Show that outer billiards relative to a regular polygonRegular polygonA regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
has almost every orbit periodic. The cases of the equilaterial triangle and the square are trivial, and Tabachnikov answered this for the regular pentagon. These are the
only cases known.
- more broadly, characterize the structure of the set of periodic orbits relative to the typical convex polygonConvex polygonIn geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
.
- understand the structure of periodic orbits relative to simple shapes in the hyperbolic plane, such as small equilateral triangles.

