
Linear dynamical system
Encyclopedia
Linear dynamical systems are a special type of dynamical system
where the equation governing the system's evolution is linear
. While dynamical systems in general do not have closed-form solutions, linear dynamical systems can be solved exactly, and they have a rich set of mathematical properties. Linear systems can also be used to understand the qualitative behavior of general linear systems, by calculating the equilibrium points of the system and approximating it as a linear system around each such point.
(an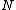 -dimensional vector
-dimensional vector
denoted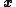 ) equals a constant matrix
) equals a constant matrix
(denoted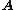 ) multiplied by
) multiplied by
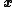 . This variation can take two forms: either
. This variation can take two forms: either
as a flow
, in which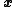 varies
varies
continuously with time
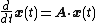
or as a mapping, in which
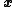 varies in discrete
varies in discrete
steps
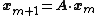
These equations are linear in the following sense: if
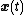 and
and 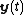
are two valid solutions, then so is any linear combination
of the two solutions, e.g.,
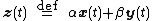
where and
and 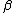
are any two scalars
. The matrix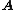
need not be symmetric.
Linear dynamical systems can be solved exactly, in contrast to most nonlinear ones. Occasionally, a nonlinear system can be solved exactly by a change of variables to a linear system. Moreover, the solutions of (almost) any nonlinear system can be well-approximated by an equivalent linear system near its fixed points
. Hence, understanding linear systems and their solutions is a crucial first step to understanding the more complex nonlinear systems.
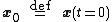
is aligned with a right eigenvector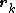 of
of
the matrix
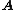 , the dynamics are simple
, the dynamics are simple
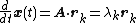
where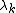 is the corresponding eigenvalue;
is the corresponding eigenvalue;
the solution of this equation is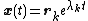
as may be confirmed by substitution.
If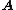 is diagonalizable
is diagonalizable
, then any vector in an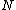 -dimensional space can be represented by a linear combination of the right and left eigenvectors (denoted
-dimensional space can be represented by a linear combination of the right and left eigenvectors (denoted 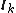 ) of the matrix
) of the matrix 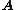 .
.
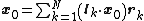
Therefore, the general solution for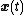 is
is
a linear combination of the individual solutions for the right
eigenvectors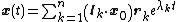
Similar considerations apply to the discrete mappings.
det(A - λI) are the eigenvalues of A. The sign and relation of these roots,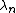 , to each other may be used to determine the stability of the dynamical system
, to each other may be used to determine the stability of the dynamical system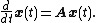
For a 2-dimensional system, the characteristic polynomial is of the form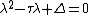 where
where  is the trace
is the trace
and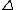 is the determinant
is the determinant
of A. Thus the two roots are in the form: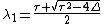
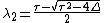
Note also that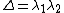 and
and 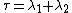 . Thus if
. Thus if 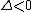 then the eigenvalues are of opposite sign, and the fixed point is a saddle. If
then the eigenvalues are of opposite sign, and the fixed point is a saddle. If 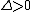 then the eigenvalues are of the same sign. Therefore if
then the eigenvalues are of the same sign. Therefore if 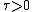 both are positive and the point is unstable, and if
both are positive and the point is unstable, and if 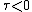 then both are negative and the point is stable. The discriminant
then both are negative and the point is stable. The discriminant
will tell you if the point is nodal or spiral (i.e. if the eigenvalues are real or complex).
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
where the equation governing the system's evolution is linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
. While dynamical systems in general do not have closed-form solutions, linear dynamical systems can be solved exactly, and they have a rich set of mathematical properties. Linear systems can also be used to understand the qualitative behavior of general linear systems, by calculating the equilibrium points of the system and approximating it as a linear system around each such point.
Introduction
In a linear dynamical system, the variation of a state vector(an
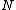 -dimensional vector
-dimensional vectorVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
denoted
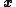 ) equals a constant matrix
) equals a constant matrix(denoted
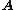 ) multiplied by
) multiplied by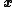 . This variation can take two forms: either
. This variation can take two forms: eitheras a flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
, in which
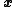 varies
variescontinuously with time
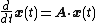
or as a mapping, in which
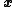 varies in discrete
varies in discreteDiscrete time
Discrete time is the discontinuity of a function's time domain that results from sampling a variable at a finite interval. For example, consider a newspaper that reports the price of crude oil once every day at 6:00AM. The newspaper is described as sampling the cost at a frequency of once per 24...
steps
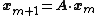
These equations are linear in the following sense: if
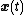 and
and 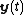
are two valid solutions, then so is any linear combination
of the two solutions, e.g.,
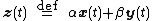
where
 and
and 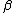
are any two scalars
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
. The matrix
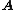
need not be symmetric.
Linear dynamical systems can be solved exactly, in contrast to most nonlinear ones. Occasionally, a nonlinear system can be solved exactly by a change of variables to a linear system. Moreover, the solutions of (almost) any nonlinear system can be well-approximated by an equivalent linear system near its fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
. Hence, understanding linear systems and their solutions is a crucial first step to understanding the more complex nonlinear systems.
Solution of linear dynamical systems
If the initial vector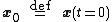
is aligned with a right eigenvector
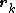 of
ofthe matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
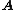 , the dynamics are simple
, the dynamics are simple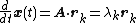
where
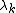 is the corresponding eigenvalue;
is the corresponding eigenvalue;the solution of this equation is
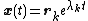
as may be confirmed by substitution.
If
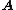 is diagonalizable
is diagonalizableDiagonalizable matrix
In linear algebra, a square matrix A is called diagonalizable if it is similar to a diagonal matrix, i.e., if there exists an invertible matrix P such that P −1AP is a diagonal matrix...
, then any vector in an
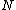 -dimensional space can be represented by a linear combination of the right and left eigenvectors (denoted
-dimensional space can be represented by a linear combination of the right and left eigenvectors (denoted 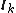 ) of the matrix
) of the matrix 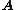 .
.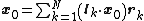
Therefore, the general solution for
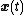 is
isa linear combination of the individual solutions for the right
eigenvectors
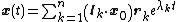
Similar considerations apply to the discrete mappings.
Classification in two dimensions
The roots of the characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
det(A - λI) are the eigenvalues of A. The sign and relation of these roots,
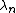 , to each other may be used to determine the stability of the dynamical system
, to each other may be used to determine the stability of the dynamical system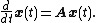
For a 2-dimensional system, the characteristic polynomial is of the form
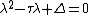 where
where  is the trace
is the traceTrace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
and
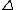 is the determinant
is the determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of A. Thus the two roots are in the form:
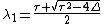
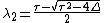
Note also that
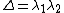 and
and 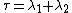 . Thus if
. Thus if 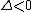 then the eigenvalues are of opposite sign, and the fixed point is a saddle. If
then the eigenvalues are of opposite sign, and the fixed point is a saddle. If 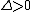 then the eigenvalues are of the same sign. Therefore if
then the eigenvalues are of the same sign. Therefore if 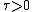 both are positive and the point is unstable, and if
both are positive and the point is unstable, and if 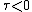 then both are negative and the point is stable. The discriminant
then both are negative and the point is stable. The discriminantDiscriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
will tell you if the point is nodal or spiral (i.e. if the eigenvalues are real or complex).

