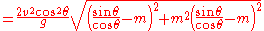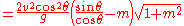Trajectory
Encyclopedia
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile
or a satellite
, for example. It thus includes the meaning of orbit
—the path of a planet
, an asteroid
or a comet
as it travels around a central mass. A trajectory can be described mathematically either by the geometry of the path, or as the position of the object over time.
In control theory
a trajectory is a time-ordered set of states of a dynamical system
(see e.g. Poincaré map
). In discrete mathematics
, a trajectory is a sequence
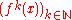 of values calculated by the iterated application of a mapping
of values calculated by the iterated application of a mapping
 to an element
to an element  of its source.
of its source.
. In this simple approximation the trajectory takes the shape of a parabola
. Generally, when determining trajectories it may be necessary to account for nonuniform gravitational forces, air resistance (drag
and aerodynamics
). This is the focus of the discipline of ballistics
.
One of the remarkable achievements of Newtonian mechanics was the derivation of the laws of Kepler, in the case of the gravitational field of a single point mass (representing the Sun
). The trajectory is a conic section
, like an ellipse
or a parabola
. This agrees with the observed orbits of planets and comets, to a reasonably good approximation, although if a comet passes close to the Sun, then it is also influenced by other force
s, such as the solar wind
and radiation pressure
, which modify the orbit, and cause the comet to eject material into space.
Newton's theory later developed into the branch of theoretical physics
known as classical mechanics
. It employs the mathematics of differential calculus
(which was, in fact, also initiated by Newton, in his youth). Over the centuries, countless scientists contributed to the development of these two disciplines. Classical mechanics became a most prominent demonstration of the power of rational thought, i.e. reason
, in science as well as technology. It helps to understand and predict an enormous range of phenomena. Trajectories are but one example.
Consider a particle of mass
 , moving in a potential field
, moving in a potential field  . Physically speaking, mass represents inertia
. Physically speaking, mass represents inertia
, and the field represents external forces, of a particular kind known as "conservative". That is, given
represents external forces, of a particular kind known as "conservative". That is, given  at every relevant position, there is a way to infer the associated force that would act at that position, say from gravity. Not all forces can be expressed in this way, however.
at every relevant position, there is a way to infer the associated force that would act at that position, say from gravity. Not all forces can be expressed in this way, however.
The motion of the particle is described by the second-order differential equation
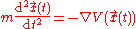 with
with 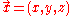
On the right-hand side, the force is given in terms of , the gradient
, the gradient
of the potential, taken at positions along the trajectory. This is the mathematical form of Newton's second law of motion: force equals mass times acceleration, for such situations.
 The ideal case of motion of a projectile in a uniform gravitational field, in the absence of other forces(such as air drag), was first investigated by Galileo Galilei
The ideal case of motion of a projectile in a uniform gravitational field, in the absence of other forces(such as air drag), was first investigated by Galileo Galilei
. To neglect the action of the atmosphere, in shaping a trajectory, would have been considered a futile hypothesis by practical minded investigators, all through the Middle Ages
in Europe
. Nevertheless, by anticipating the existence of the vacuum
, later to be demonstrated on Earth by his collaborator Evangelista Torricelli
, Galileo was able to initiate the future science of mechanics
. And in a near vacuum, as it turns out for instance on the Moon
, his simplified parabolic trajectory proves essentially correct.
In the analysis that follows we derive the equation of motion of a projectile as measured from an inertial frame, at rest with respect to the ground, to which frame is associated a right-hand co-ordinate system - the origin of which coincides with the point of launch of the projectile. The x-axis is parallel to the ground and the y axis perpendicular to it ( parallel to the gravitational field lines ). Let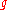 be the acceleration of gravity
be the acceleration of gravity
. Relative to the flat terrain, let the initial horizontal speed be and the initial vertical speed be
and the initial vertical speed be  . It will also be shown that, the range
. It will also be shown that, the range
is , and the maximum altitude is
, and the maximum altitude is  ; The maximum range, for a given initial speed
; The maximum range, for a given initial speed  , is obtained when
, is obtained when  , i.e. the initial angle is 45 degrees. This range is
, i.e. the initial angle is 45 degrees. This range is 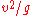 , and the maximum altitude at the maximum range is a quarter of that.
, and the maximum altitude at the maximum range is a quarter of that.
frame which happens to be at (x,y)=(0,0) at t=0. The equation of motion of the projectile in this frame ( by the principle of equivalence) would be . The co-ordinates of this free-fall frame, with respect to our inertial frame would be
. The co-ordinates of this free-fall frame, with respect to our inertial frame would be 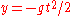 . That is,
. That is,  .
.
Now translating back to the inertial frame the co-ordinates of the projectile becomes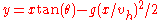 That is:
That is:
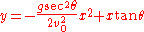 ,
,
(where v0 is the initial velocity,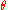 is the angle of elevation, and g is the acceleration due to gravity).
is the angle of elevation, and g is the acceleration due to gravity).

The height, h, is the greatest parabolic height said object reaches within its trajectory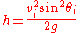
 and initial speed
and initial speed  :
:
giving the range as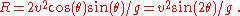
This equation can be rearranged to find the angle for a required range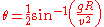 (Equation II: angle of projectile launch)
(Equation II: angle of projectile launch)
Note that the sine
function is such that there are two solutions for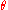 for a given range
for a given range  . The angle
. The angle 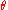 giving the maximum range can be found by considering the derivative or
giving the maximum range can be found by considering the derivative or  with respect to
with respect to  and setting it to zero.
and setting it to zero.
which has a non trivial solution at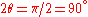 , or
, or  .
.
The maximum range is then . At this angle
. At this angle 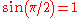 , so the maximum height obtained is
, so the maximum height obtained is 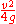 .
.
To find the angle giving the maximum height for a given speed calculate the derivative of the maximum height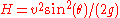 with respect to
with respect to 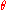 , that is
, that is
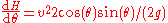
which is zero when . So the maximum height
. So the maximum height 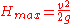 is obtained when the projectile is fired straight up.
is obtained when the projectile is fired straight up.
 and launch angle
and launch angle 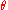 as before, it can be shown that the range along the hill
as before, it can be shown that the range along the hill  forms a ratio with the original range
forms a ratio with the original range  along the imaginary horizontal, such that:
along the imaginary horizontal, such that: (Equation 11)
(Equation 11)
In this equation, downhill occurs when is between 0 and -90 degrees. For this range of
is between 0 and -90 degrees. For this range of  we know:
we know: 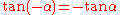 and
and 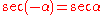 . Thus for this range of
. Thus for this range of  ,
,
 . Thus
. Thus 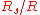 is a positive value meaning the range downhill is always further than along level terrain. The lower level of terrain causes the projectile to remain in the air longer, allowing it to travel further horizontally before hitting the ground.
is a positive value meaning the range downhill is always further than along level terrain. The lower level of terrain causes the projectile to remain in the air longer, allowing it to travel further horizontally before hitting the ground.
While the same equation applies to projectiles fired uphill, the interpretation is more complex as sometimes the uphill range may be shorter or longer than the equivalent range along level terrain. Equation 11 may be set to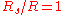 (i.e. the slant range is equal to the level terrain range) and solving for the "critical angle"
(i.e. the slant range is equal to the level terrain range) and solving for the "critical angle" 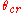 :
:
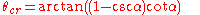
Equation 11 may also be used to develop the "rifleman's rule
" for small values of and
and 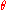 (i.e. close to horizontal firing, which is the case for many firearm situations). For small values, both
(i.e. close to horizontal firing, which is the case for many firearm situations). For small values, both  and
and  have a small value and thus when multiplied together (as in equation 11), the result is almost zero. Thus equation 11 may be approximated as:
have a small value and thus when multiplied together (as in equation 11), the result is almost zero. Thus equation 11 may be approximated as:
And solving for level terrain range,
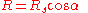 "Rifleman's rule"
"Rifleman's rule"
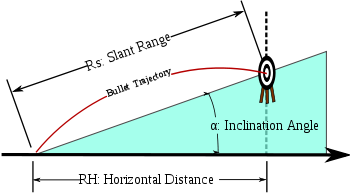
Thus if the shooter attempts to hit the level distance R, s/he will actually hit the slant target. "In other words, pretend that the inclined target is at a horizontal distance equal to the slant range distance multiplied by the cosine of the inclination angle, and aim as if the target were really at that horizontal position."http://www.snipertools.com/article4.htm
 in standard linear form at coordinates
in standard linear form at coordinates  :
: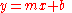 (Equation 12) where in this case,
(Equation 12) where in this case,  ,
,  and
and 
Substituting the value of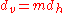 into Equation 10:
into Equation 10: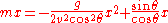
 (Solving above x)
(Solving above x)
This value of x may be substituted back into the linear equation 12 to get the corresponding y coordinate at the intercept: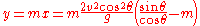
Now the slant range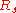 is the distance of the intercept from the origin, which is just the hypotenuse
is the distance of the intercept from the origin, which is just the hypotenuse
of x and y: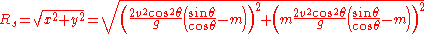
Now is defined as the angle of the hill, so by definition of tangent,
is defined as the angle of the hill, so by definition of tangent,  . This can be substituted into the equation for
. This can be substituted into the equation for 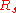 :
: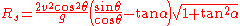
Now this can be refactored and the trigonometric identity for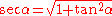 may be used:
may be used: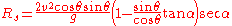
Now the flat range by the previously used trigonometric identity and
by the previously used trigonometric identity and  so:
so:

two bodies orbiting with the mutual gravitation between them, we obtain
Kepler's laws of planetary motion
. The derivation of these was one of the major works of Isaac Newton
and provided much of the motivation for the development of differential calculus
.
Projectile
A projectile is any object projected into space by the exertion of a force. Although a thrown baseball is technically a projectile too, the term more commonly refers to a weapon....
or a satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
, for example. It thus includes the meaning of orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
—the path of a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
, an asteroid
Asteroid
Asteroids are a class of small Solar System bodies in orbit around the Sun. They have also been called planetoids, especially the larger ones...
or a comet
Comet
A comet is an icy small Solar System body that, when close enough to the Sun, displays a visible coma and sometimes also a tail. These phenomena are both due to the effects of solar radiation and the solar wind upon the nucleus of the comet...
as it travels around a central mass. A trajectory can be described mathematically either by the geometry of the path, or as the position of the object over time.
In control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
a trajectory is a time-ordered set of states of a dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
(see e.g. Poincaré map
Poincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
). In discrete mathematics
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
, a trajectory is a sequence
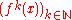 of values calculated by the iterated application of a mapping
of values calculated by the iterated application of a mapping to an element
to an element  of its source.
of its source.
Physics of trajectories
A familiar example of a trajectory is is the path of a projectile such as a thrown ball or rock. In a greatly simplified model the object moves only under the influence of a uniform homogenous gravitational force field. This can be a good approximation for a rock that is thrown for short distances for example, at the surface of the moonMoon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
. In this simple approximation the trajectory takes the shape of a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. Generally, when determining trajectories it may be necessary to account for nonuniform gravitational forces, air resistance (drag
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
and aerodynamics
Aerodynamics
Aerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
). This is the focus of the discipline of ballistics
Ballistics
Ballistics is the science of mechanics that deals with the flight, behavior, and effects of projectiles, especially bullets, gravity bombs, rockets, or the like; the science or art of designing and accelerating projectiles so as to achieve a desired performance.A ballistic body is a body which is...
.
One of the remarkable achievements of Newtonian mechanics was the derivation of the laws of Kepler, in the case of the gravitational field of a single point mass (representing the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
). The trajectory is a conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
, like an ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
or a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. This agrees with the observed orbits of planets and comets, to a reasonably good approximation, although if a comet passes close to the Sun, then it is also influenced by other force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s, such as the solar wind
Solar wind
The solar wind is a stream of charged particles ejected from the upper atmosphere of the Sun. It mostly consists of electrons and protons with energies usually between 1.5 and 10 keV. The stream of particles varies in temperature and speed over time...
and radiation pressure
Radiation pressure
Radiation pressure is the pressure exerted upon any surface exposed to electromagnetic radiation. If absorbed, the pressure is the power flux density divided by the speed of light...
, which modify the orbit, and cause the comet to eject material into space.
Newton's theory later developed into the branch of theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
known as classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
. It employs the mathematics of differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
(which was, in fact, also initiated by Newton, in his youth). Over the centuries, countless scientists contributed to the development of these two disciplines. Classical mechanics became a most prominent demonstration of the power of rational thought, i.e. reason
Reason
Reason is a term that refers to the capacity human beings have to make sense of things, to establish and verify facts, and to change or justify practices, institutions, and beliefs. It is closely associated with such characteristically human activities as philosophy, science, language, ...
, in science as well as technology. It helps to understand and predict an enormous range of phenomena. Trajectories are but one example.
Consider a particle of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
 , moving in a potential field
, moving in a potential field  . Physically speaking, mass represents inertia
. Physically speaking, mass represents inertiaInertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
, and the field
 represents external forces, of a particular kind known as "conservative". That is, given
represents external forces, of a particular kind known as "conservative". That is, given  at every relevant position, there is a way to infer the associated force that would act at that position, say from gravity. Not all forces can be expressed in this way, however.
at every relevant position, there is a way to infer the associated force that would act at that position, say from gravity. Not all forces can be expressed in this way, however.The motion of the particle is described by the second-order differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
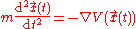 with
with 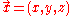
On the right-hand side, the force is given in terms of
 , the gradient
, the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the potential, taken at positions along the trajectory. This is the mathematical form of Newton's second law of motion: force equals mass times acceleration, for such situations.
Uniform gravity, no drag or wind

Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
. To neglect the action of the atmosphere, in shaping a trajectory, would have been considered a futile hypothesis by practical minded investigators, all through the Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
in Europe
Europe
Europe is, by convention, one of the world's seven continents. Comprising the westernmost peninsula of Eurasia, Europe is generally 'divided' from Asia to its east by the watershed divides of the Ural and Caucasus Mountains, the Ural River, the Caspian and Black Seas, and the waterways connecting...
. Nevertheless, by anticipating the existence of the vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
, later to be demonstrated on Earth by his collaborator Evangelista Torricelli
Evangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
, Galileo was able to initiate the future science of mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
. And in a near vacuum, as it turns out for instance on the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
, his simplified parabolic trajectory proves essentially correct.
In the analysis that follows we derive the equation of motion of a projectile as measured from an inertial frame, at rest with respect to the ground, to which frame is associated a right-hand co-ordinate system - the origin of which coincides with the point of launch of the projectile. The x-axis is parallel to the ground and the y axis perpendicular to it ( parallel to the gravitational field lines ). Let
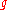 be the acceleration of gravity
be the acceleration of gravityStandard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
. Relative to the flat terrain, let the initial horizontal speed be
 and the initial vertical speed be
and the initial vertical speed be  . It will also be shown that, the range
. It will also be shown that, the rangeRange of a projectile
right|thumb|250 px|The path of this projectile launched from a height y0 has a range d.In physics, assuming a flat Earth with a uniform gravity field, a projectile launched with specific initial conditions will have a predictable range. As in Trajectory of a projectile, we will use:The following...
is
 , and the maximum altitude is
, and the maximum altitude is  ; The maximum range, for a given initial speed
; The maximum range, for a given initial speed  , is obtained when
, is obtained when  , i.e. the initial angle is 45 degrees. This range is
, i.e. the initial angle is 45 degrees. This range is 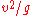 , and the maximum altitude at the maximum range is a quarter of that.
, and the maximum altitude at the maximum range is a quarter of that.Derivation of the equation of motion
Assume the motion of the projectile is being measured from a Free fallFree fall
Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
frame which happens to be at (x,y)=(0,0) at t=0. The equation of motion of the projectile in this frame ( by the principle of equivalence) would be
 . The co-ordinates of this free-fall frame, with respect to our inertial frame would be
. The co-ordinates of this free-fall frame, with respect to our inertial frame would be 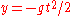 . That is,
. That is,  .
.Now translating back to the inertial frame the co-ordinates of the projectile becomes
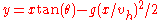 That is:
That is: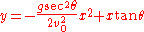 ,
,(where v0 is the initial velocity,
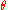 is the angle of elevation, and g is the acceleration due to gravity).
is the angle of elevation, and g is the acceleration due to gravity).Range and height
The range, R, is the greatest distance the object travels along the x-axis in the I sector. The initial velocity, vi, is the speed at which said object is launched from the point of origin. The initial angle, θi, is the angle at which said object is released. The g is the respective gravitational pull on the object within a null-medium.
The height, h, is the greatest parabolic height said object reaches within its trajectory
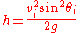
Angle of elevation
In terms of angle of elevation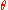 and initial speed
and initial speed  :
:
giving the range as
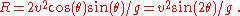
This equation can be rearranged to find the angle for a required range
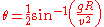 (Equation II: angle of projectile launch)
(Equation II: angle of projectile launch)Note that the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
function is such that there are two solutions for
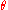 for a given range
for a given range  . The angle
. The angle 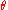 giving the maximum range can be found by considering the derivative or
giving the maximum range can be found by considering the derivative or  with respect to
with respect to  and setting it to zero.
and setting it to zero.
which has a non trivial solution at
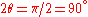 , or
, or  .
.The maximum range is then
 . At this angle
. At this angle 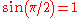 , so the maximum height obtained is
, so the maximum height obtained is 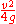 .
.To find the angle giving the maximum height for a given speed calculate the derivative of the maximum height
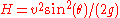 with respect to
with respect to 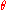 , that is
, that is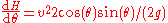
which is zero when
 . So the maximum height
. So the maximum height 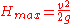 is obtained when the projectile is fired straight up.
is obtained when the projectile is fired straight up.Uphill/downhill in uniform gravity in a vacuum
Given a hill angle and launch angle
and launch angle 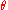 as before, it can be shown that the range along the hill
as before, it can be shown that the range along the hill  forms a ratio with the original range
forms a ratio with the original range  along the imaginary horizontal, such that:
along the imaginary horizontal, such that: (Equation 11)
(Equation 11)In this equation, downhill occurs when
 is between 0 and -90 degrees. For this range of
is between 0 and -90 degrees. For this range of  we know:
we know: 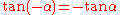 and
and 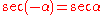 . Thus for this range of
. Thus for this range of  ,
, . Thus
. Thus 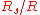 is a positive value meaning the range downhill is always further than along level terrain. The lower level of terrain causes the projectile to remain in the air longer, allowing it to travel further horizontally before hitting the ground.
is a positive value meaning the range downhill is always further than along level terrain. The lower level of terrain causes the projectile to remain in the air longer, allowing it to travel further horizontally before hitting the ground.While the same equation applies to projectiles fired uphill, the interpretation is more complex as sometimes the uphill range may be shorter or longer than the equivalent range along level terrain. Equation 11 may be set to
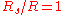 (i.e. the slant range is equal to the level terrain range) and solving for the "critical angle"
(i.e. the slant range is equal to the level terrain range) and solving for the "critical angle" 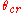 :
:
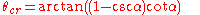
Equation 11 may also be used to develop the "rifleman's rule
Rifleman's rule
Rifleman's rule is a "rule of thumb" that allows a rifleman to accurately fire a rifle that has been calibrated for horizontal targets at uphill or downhill targets. The rule provides an equivalent horizontal range setting for engaging a target at a known uphill or downhill distance from the rifle...
" for small values of
 and
and 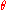 (i.e. close to horizontal firing, which is the case for many firearm situations). For small values, both
(i.e. close to horizontal firing, which is the case for many firearm situations). For small values, both  and
and  have a small value and thus when multiplied together (as in equation 11), the result is almost zero. Thus equation 11 may be approximated as:
have a small value and thus when multiplied together (as in equation 11), the result is almost zero. Thus equation 11 may be approximated as:
And solving for level terrain range,

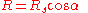 "Rifleman's rule"
"Rifleman's rule"Thus if the shooter attempts to hit the level distance R, s/he will actually hit the slant target. "In other words, pretend that the inclined target is at a horizontal distance equal to the slant range distance multiplied by the cosine of the inclination angle, and aim as if the target were really at that horizontal position."http://www.snipertools.com/article4.htm
Derivation based on equations of a parabola
The intersect of the projectile trajectory with a hill may most easily be derived using the trajectory in parabolic form in Cartesian coordinates (Equation 10) intersecting the hill of slope in standard linear form at coordinates
in standard linear form at coordinates  :
: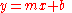 (Equation 12) where in this case,
(Equation 12) where in this case,  ,
,  and
and 
Substituting the value of
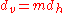 into Equation 10:
into Equation 10: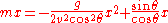
 (Solving above x)
(Solving above x)This value of x may be substituted back into the linear equation 12 to get the corresponding y coordinate at the intercept:
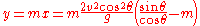
Now the slant range
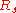 is the distance of the intercept from the origin, which is just the hypotenuse
is the distance of the intercept from the origin, which is just the hypotenuseHypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
of x and y:
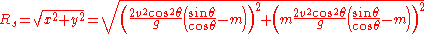
Now
 is defined as the angle of the hill, so by definition of tangent,
is defined as the angle of the hill, so by definition of tangent,  . This can be substituted into the equation for
. This can be substituted into the equation for 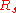 :
: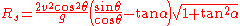
Now this can be refactored and the trigonometric identity for
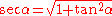 may be used:
may be used: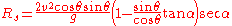
Now the flat range
 by the previously used trigonometric identity and
by the previously used trigonometric identity and  so:
so:

Orbiting objects
If instead of a uniform downwards gravitational force we considertwo bodies orbiting with the mutual gravitation between them, we obtain
Kepler's laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
. The derivation of these was one of the major works of Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and provided much of the motivation for the development of differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
.
See also
- Aft-crossing trajectoryAft-crossing trajectoryIn 2005, a new trajectory that an air-launched rocket could take to put satellites into orbit was tested. Until this time, launch vehicles such as the Pegasus rocket, or rocket planes such as the X-1, X-15, or SpaceShipOne, which were carried under an aircraft pointing in the same direction as the...
- Orbit (dynamics)Orbit (dynamics)In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
- Orbit (group theory)
- Planetary orbitPlanetary orbitIn physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
- Porkchop plotPorkchop plotPorkchop plot is a chart that shows contours of equal characteristic energy against combinations of launch date and arrival date for a particular interplanetary flight....
- Range of a projectileRange of a projectileright|thumb|250 px|The path of this projectile launched from a height y0 has a range d.In physics, assuming a flat Earth with a uniform gravity field, a projectile launched with specific initial conditions will have a predictable range. As in Trajectory of a projectile, we will use:The following...
- Rigid bodyRigid bodyIn physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
- Trajectory of a projectileTrajectory of a projectileIn physics, the ballistic trajectory of a projectile is the path that a thrown or launched projectile will take under the action of gravity, neglecting all other forces, such as friction from air resistance, without propulsion....
External links
- Projectile Motion Flash Applet
- Trajectory calculator
- An interactive simulation on projectile motion
- Projectile Motion Simulator, java applet
- Projectile Lab, JavaScript trajectory simulator
- Parabolic Projectile Motion: Shooting a Harmless Tranquilizer Dart at a Falling Monkey by Roberto Castilla-Meléndez, Roxana Ramírez-Herrera, and José Luis Gómez-Muñoz, The Wolfram Demonstrations Project.
- Trajectory, ScienceWorld.
- Java projectile-motion simulation, with first-order air resistance.
- Java projectile-motion simulation; targeting solutions, parabola of safety.