
Poincaré recurrence theorem
Encyclopedia
In mathematics
, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which energy
is conserved. The theorem is commonly discussed in the context of ergodic theory
, dynamical systems and statistical mechanics
.
The theorem is named after Henri Poincaré
, who published it in 1890.
defined by an ordinary differential equation
determines a flow map
f t mapping phase space
on itself. The system is said to be volume-preserving if the volume of a set in phase space is invariant under the flow. For instance, all Hamiltonian system
s are volume-preserving because of Liouville's theorem
. The theorem is then: If a flow
preserves volume and has only bounded orbits, then for each open set there exist orbits that intersect the set infinitely often.
As an example, the deterministic baker's map
exhibits Poincaré recurrence which can be demonstrated in a particularly dramatic fashion when acting on 2D images. A given image, when sliced and squashed hundreds of times, turns into a snow of apparent "random noise". However, when the process is repeated thousands of times, the image reappears, although at times marred with greater or lesser bits of noise.
Imagine an arbitrary small neighborhood of any point in the phase space
and follow its path under dynamics of the system (usually called a "phase tube"). The volume "sweeps" points of phase space as it moves. It can never cross the regions that are already "swept", because phase trajectories do not intersect. Hence, the total volume accessible to it constantly decreases, and since the total volume is finite by assumption, in a finite time, all volume will be exhausted. At that point, the only way to continue would be for the phase tube to connect to its own starting point, which is QED.
Note that individual trajectories included in the phase tube need not connect to their respective starting points, most likely they will all be mixed up within the tube. This is why recurrence is only approximate up to the diameter of the tube. To achieve greater accuracy of recurrence, we need to take smaller initial volume, which means longer recurrence time.
Note also that nothing prevents the system from returning to its starting point before all the phase volume is exhausted. A trivial example of this is the harmonic oscillator
. Systems that do cover all available phase volume are called ergodic
.
 be a finite measure space and let
be a finite measure space and let 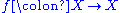
be a measure-preserving transformation. Below are two alternative statements of the theorem.
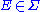 , the set of those points
, the set of those points  of
of  such that
such that  for all
for all  has zero measure. That is, almost every point of
has zero measure. That is, almost every point of  returns to
returns to  . In fact, almost every point returns infinitely often; i.e.
. In fact, almost every point returns infinitely often; i.e.
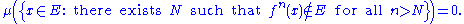
For a proof, see .
If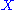 is a second-countable Hausdorff space
is a second-countable Hausdorff space
and contains the Borel sigma-algebra, then the set of recurrent points of
contains the Borel sigma-algebra, then the set of recurrent points of 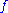 has full measure. That is, almost every point is recurrent.
has full measure. That is, almost every point is recurrent.
For a proof, see
 and
and 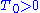 there exists a time T larger than
there exists a time T larger than  , such that
, such that  , where
, where 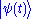 denotes the state vector of the system at time t.
denotes the state vector of the system at time t.
The essential elements of the proof are as follows. The system evolves in time according to:
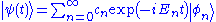
where the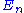 are the energy eigenvalues (we use natural units, so
are the energy eigenvalues (we use natural units, so  ), and the
), and the 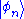 are the energy eigenstates. The squared norm of the difference of the state vector at time T and time zero, can be written as:
are the energy eigenstates. The squared norm of the difference of the state vector at time T and time zero, can be written as:
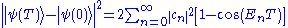
We can truncate the summation at some n = N independent of T, because
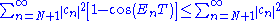
which can be made arbitrarily small because the summation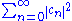 , being the squared norm of the initial state, converges to 1.
, being the squared norm of the initial state, converges to 1.
That the finite sum
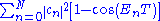
can be made arbitrarily small, follows from the existense of integers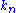 such that
such that 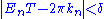 for arbitrary
for arbitrary  . This implies that there exists intervals for T on which
. This implies that there exists intervals for T on which  . On such intervals, we have:
. On such intervals, we have:
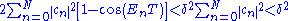
The state vector thus returns arbitrarily closely to the initial state, infinitely often.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
is conserved. The theorem is commonly discussed in the context of ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, dynamical systems and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
The theorem is named after Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, who published it in 1890.
Precise formulation
Any dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
defined by an ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
determines a flow map
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
f t mapping phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
on itself. The system is said to be volume-preserving if the volume of a set in phase space is invariant under the flow. For instance, all Hamiltonian system
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
s are volume-preserving because of Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
. The theorem is then: If a flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
preserves volume and has only bounded orbits, then for each open set there exist orbits that intersect the set infinitely often.
As an example, the deterministic baker's map
Baker's map
In dynamical systems theory, the baker's map is a chaotic map from the unit square into itself. It is named after a kneading operation that bakers apply to dough: the dough is cut in half, and the two halves are stacked on one-another, and compressed...
exhibits Poincaré recurrence which can be demonstrated in a particularly dramatic fashion when acting on 2D images. A given image, when sliced and squashed hundreds of times, turns into a snow of apparent "random noise". However, when the process is repeated thousands of times, the image reappears, although at times marred with greater or lesser bits of noise.
Discussion of proof
The proof, speaking qualitatively, hinges on two premises:- The phase trajectories of closed dynamical systemDynamical systemA dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s do not intersect. - The phase volume of a finite element under dynamics is conserved.
Imagine an arbitrary small neighborhood of any point in the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
and follow its path under dynamics of the system (usually called a "phase tube"). The volume "sweeps" points of phase space as it moves. It can never cross the regions that are already "swept", because phase trajectories do not intersect. Hence, the total volume accessible to it constantly decreases, and since the total volume is finite by assumption, in a finite time, all volume will be exhausted. At that point, the only way to continue would be for the phase tube to connect to its own starting point, which is QED.
Note that individual trajectories included in the phase tube need not connect to their respective starting points, most likely they will all be mixed up within the tube. This is why recurrence is only approximate up to the diameter of the tube. To achieve greater accuracy of recurrence, we need to take smaller initial volume, which means longer recurrence time.
Note also that nothing prevents the system from returning to its starting point before all the phase volume is exhausted. A trivial example of this is the harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
. Systems that do cover all available phase volume are called ergodic
Ergodic hypothesis
In physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...
.
Formal statement of the theorem
Let be a finite measure space and let
be a finite measure space and let 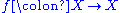
be a measure-preserving transformation. Below are two alternative statements of the theorem.
Theorem 1
For any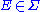 , the set of those points
, the set of those points  of
of  such that
such that  for all
for all  has zero measure. That is, almost every point of
has zero measure. That is, almost every point of  returns to
returns to  . In fact, almost every point returns infinitely often; i.e.
. In fact, almost every point returns infinitely often; i.e.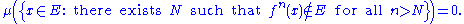
For a proof, see .
Theorem 2
The following is a topological version of this theorem:If
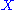 is a second-countable Hausdorff space
is a second-countable Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
and
 contains the Borel sigma-algebra, then the set of recurrent points of
contains the Borel sigma-algebra, then the set of recurrent points of 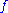 has full measure. That is, almost every point is recurrent.
has full measure. That is, almost every point is recurrent.For a proof, see
Quantum mechanical version
For quantum mechanical systems with discrete energy eigenstates, a similar theorem holds. For every and
and 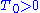 there exists a time T larger than
there exists a time T larger than  , such that
, such that  , where
, where 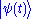 denotes the state vector of the system at time t.
denotes the state vector of the system at time t.The essential elements of the proof are as follows. The system evolves in time according to:
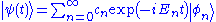
where the
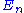 are the energy eigenvalues (we use natural units, so
are the energy eigenvalues (we use natural units, so  ), and the
), and the 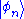 are the energy eigenstates. The squared norm of the difference of the state vector at time T and time zero, can be written as:
are the energy eigenstates. The squared norm of the difference of the state vector at time T and time zero, can be written as: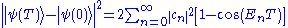
We can truncate the summation at some n = N independent of T, because
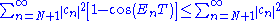
which can be made arbitrarily small because the summation
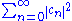 , being the squared norm of the initial state, converges to 1.
, being the squared norm of the initial state, converges to 1.That the finite sum
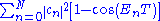
can be made arbitrarily small, follows from the existense of integers
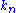 such that
such that 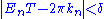 for arbitrary
for arbitrary  . This implies that there exists intervals for T on which
. This implies that there exists intervals for T on which  . On such intervals, we have:
. On such intervals, we have: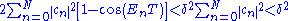
The state vector thus returns arbitrarily closely to the initial state, infinitely often.
See also
- Ergodic hypothesisErgodic hypothesisIn physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...
- Recurrence plotRecurrence plotIn descriptive statistics and chaos theory, a recurrence plot is a plot showing, for a given moment in time, the times at which a phase space trajectory visits roughly the same area in the phase space...
- Recurrence period density entropyRecurrence period density entropyRecurrence period density entropy is a method, in the fields of dynamical systems, stochastic processes, and time series analysis, for determining the periodicity, or repetitiveness of a signal.- Overview :...
- Wandering setWandering setIn those branches of mathematics called dynamical systems and ergodic theory, the concept of a wandering set formalizes a certain idea of movement and mixing in such systems. When a dynamical system has a wandering set of non-zero measure, then the system is a dissipative system...

