
Anosov diffeomorphism
Encyclopedia
In mathematics
, more particularly in the fields of dynamical systems and geometric topology
, an Anosov map on a manifold
M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A
systems.
Anosov diffeomorphisms were introduced by D. V. Anosov, who proved that their behaviour was in an appropriate sense generic (when they exist at all).
A classical example of Anosov diffeomorphism is the Arnold's cat map
.
Anosov proved that Anosov diffeomorphisms are structurally stable and form an open subset of mappings (flows) with the C1 topology.
Not every manifold admits an Anosov diffeomorphism; for example, there are no such diffeomorphisms on the sphere
. The simplest examples of compact manifolds admitting them are the tori: they admit the so-called linear Anosov diffeomorphisms, which are isomorphisms having no eigenvalue of modulus 1. It was proved that any other Anosov diffeomorphism on a torus is topologically conjugate to one of this kind.
The problem of classifying manifolds that admit Anosov diffeomorphisms turned out to be very difficult, and still has no answer. The only known examples are infranil manifolds, and it is conjectured that they are the only ones.
Another open problem is whether every Anosov diffeomorphism is transitive. All known Anosov diffeomorphisms are transitive. A sufficient condition for transitivity is nonwandering: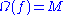 .
.
Also it is unknown if every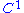 volume preserving Anosov diffeomorphism is ergodic. Anosov proved it under
volume preserving Anosov diffeomorphism is ergodic. Anosov proved it under 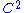 assumption. It is also true for
assumption. It is also true for 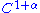 volume preserving Anosov diffeomorphisms.
volume preserving Anosov diffeomorphisms.
For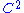 transitive Anosov diffeomorphism
transitive Anosov diffeomorphism 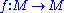 there exists a unique SRB measure (stand for Sinai, Ruelle and Bowen)
there exists a unique SRB measure (stand for Sinai, Ruelle and Bowen) 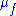 supported on
supported on  such that its basin
such that its basin 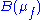 is of full volume, where
is of full volume, where 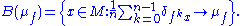
of a Riemann surface
of negative curvature
. This flow can be understood in terms of the flow on the tangent bundle of the Poincare half-plane model
of hyperbolic geometry. Riemann surfaces of negative curvature may be defined as Fuchsian model
s, that is, as the quotients of the upper half-plane and a Fuchsian group
. For the following, let H be the upper half-plane; let Γ be a Fuchsian group; let M=H\Γ be a Riemann surface of negative curvature, and let T1M be the tangent bundle of unit-length vectors on the manifold M, and let T1H be the tangent bundle of unit-length vectors on H. Note that a bundle of unit-length vectors on a surface is the principal bundle
of a complex line bundle
.
PSL(2,R). This group is the group of orientation-preserving isometries of the upper half-plane. The Lie algebra
of PSL(2,R) is sl(2,R), and is represented by the matrices
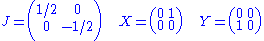
which have the algebra

The exponential map
s
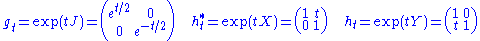
define right-invariant flow
s on the manifold of T1H=PSL(2,R), and likewise on T1M. Defining P=T1H and Q=T1M, these flows define vector fields on P and Q, whose vectors lie in TP and TQ. These are just the standard, ordinary Lie vector fields on the manifold of a Lie group, and the presentation above is a standard exposition of a Lie vector field.
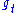 is the geodesic flow on P and Q. Lie vector fields being (by definition) left invariant under the action of a group element, one has that these fields are left invariant under the specific elements
is the geodesic flow on P and Q. Lie vector fields being (by definition) left invariant under the action of a group element, one has that these fields are left invariant under the specific elements 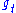 of the geodesic flow. In other words, the spaces TP and TQ are split into three one-dimensional spaces, or subbundle
of the geodesic flow. In other words, the spaces TP and TQ are split into three one-dimensional spaces, or subbundle
s, each of which are invariant under the geodesic flow. The final step is to notice that vector fields in one subbundle expand (and expand exponentially), those in another are unchanged, and those in a third shrink (and do so exponentially).
More precisely, the tangent bundle TQ may be written as the direct sum
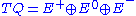
or, at a point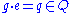 , the direct sum
, the direct sum
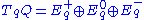
corresponding to the Lie algebra generators Y, J and X, respectively, carried, by the left action of group element g, from the origin e to the point q. That is, one has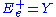 ,
, 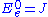 and
and 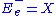 . These spaces are each subbundle
. These spaces are each subbundle
s, and are preserved (are invariant) under the action of the geodesic flow; that is, under the action of group elements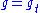 .
.
To compare the lengths of vectors in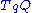 at different points q, one needs a metric. Any inner product at
at different points q, one needs a metric. Any inner product at 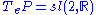 extends to a left-invariant Riemannian metric on P, and thus to a Riemannian metric on Q. The length of a vector
extends to a left-invariant Riemannian metric on P, and thus to a Riemannian metric on Q. The length of a vector 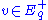 expands exponentially as exp(t) under the action of
expands exponentially as exp(t) under the action of 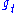 . The length of a vector
. The length of a vector 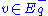 shrinks exponentially as exp(-t) under the action of
shrinks exponentially as exp(-t) under the action of 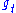 . Vectors in
. Vectors in 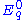 are unchanged. This may be seen by examining how the group elements commute. The geodesic flow is invariant,
are unchanged. This may be seen by examining how the group elements commute. The geodesic flow is invariant,
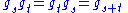
but the other two shrink and expand:

and
where we recall that a tangent vector in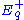 is given by the derivative
is given by the derivative
, with respect to t, of the curve
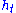 , the setting t=0.
, the setting t=0.
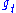 corresponds to a geodesic
corresponds to a geodesic
on the upper half plane, passing through the point z=i. The action is the standard Möbius transformation action of SL(2,R) on the upper half-plane, so that

A general geodesic is given by
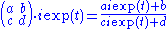
with a, b, c and d real, with ad-bc=1. The curves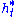 and
and 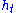 are called horocycles
are called horocycles
. Horocycles correspond to the motion of the normal vectors of a horosphere on the upper half-plane.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more particularly in the fields of dynamical systems and geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, an Anosov map on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A
Axiom A
In mathematics, Smale's axiom A defines a class of dynamical systems which have been extensively studied and whose dynamics is relatively well understood. A prominent example is the Smale horseshoe map. The term "axiom A" originates with Stephen Smale...
systems.
Anosov diffeomorphisms were introduced by D. V. Anosov, who proved that their behaviour was in an appropriate sense generic (when they exist at all).
Overview
Three closely related definitions must be distinguished:- If a differentiable mapMap (mathematics)In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
f on M has a hyperbolic structureHyperbolic setIn dynamical systems theory, a subset Λ of a smooth manifold M is said to have a hyperbolic structure with respect to a smooth map f if its tangent bundle may be split into two invariant subbundles, one of which is contracting and the other is expanding under f, with respect to some...
on the tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
, then it is called an Anosov map. Examples include the Bernoulli map, and Arnold's cat mapArnold's cat mapIn mathematics, Arnold's cat map is a chaotic map from the torus into itself, named after Vladimir Arnold, who demonstrated its effects in the 1960s using an image of a cat, hence the name....
.
- If the map is a diffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
, then it is called an Anosov diffeomorphism.
- If a flowFlow (mathematics)In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
on a manifold splits the tangent bundle into three invariant subbundleSubbundleIn mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
s, with one subbundle that is exponentially contracting, and one that is exponentially expanding, and a third, non-expanding, non-contracting one-dimensional sub-bundle (spanned by the flow direction), then the flow is called an Anosov flow.
A classical example of Anosov diffeomorphism is the Arnold's cat map
Arnold's cat map
In mathematics, Arnold's cat map is a chaotic map from the torus into itself, named after Vladimir Arnold, who demonstrated its effects in the 1960s using an image of a cat, hence the name....
.
Anosov proved that Anosov diffeomorphisms are structurally stable and form an open subset of mappings (flows) with the C1 topology.
Not every manifold admits an Anosov diffeomorphism; for example, there are no such diffeomorphisms on the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. The simplest examples of compact manifolds admitting them are the tori: they admit the so-called linear Anosov diffeomorphisms, which are isomorphisms having no eigenvalue of modulus 1. It was proved that any other Anosov diffeomorphism on a torus is topologically conjugate to one of this kind.
The problem of classifying manifolds that admit Anosov diffeomorphisms turned out to be very difficult, and still has no answer. The only known examples are infranil manifolds, and it is conjectured that they are the only ones.
Another open problem is whether every Anosov diffeomorphism is transitive. All known Anosov diffeomorphisms are transitive. A sufficient condition for transitivity is nonwandering:
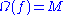 .
.Also it is unknown if every
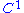 volume preserving Anosov diffeomorphism is ergodic. Anosov proved it under
volume preserving Anosov diffeomorphism is ergodic. Anosov proved it under 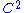 assumption. It is also true for
assumption. It is also true for 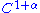 volume preserving Anosov diffeomorphisms.
volume preserving Anosov diffeomorphisms.For
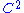 transitive Anosov diffeomorphism
transitive Anosov diffeomorphism 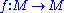 there exists a unique SRB measure (stand for Sinai, Ruelle and Bowen)
there exists a unique SRB measure (stand for Sinai, Ruelle and Bowen) 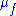 supported on
supported on  such that its basin
such that its basin 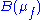 is of full volume, where
is of full volume, where 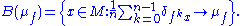
Anosov flow on (tangent bundles of) Riemann surfaces
As an example, this section develops the case of the Anosov flow on the tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
of negative curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
. This flow can be understood in terms of the flow on the tangent bundle of the Poincare half-plane model
Poincaré half-plane model
In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
of hyperbolic geometry. Riemann surfaces of negative curvature may be defined as Fuchsian model
Fuchsian model
In mathematics, a Fuchsian model is a construction of a hyperbolic Riemann surface R as a quotient of the upper half-plane H. By the uniformization theorem, every Riemann surface is either elliptic, parabolic or hyperbolic. Every hyperbolic Riemann surface has a non-trivial fundamental group \pi_1...
s, that is, as the quotients of the upper half-plane and a Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
. For the following, let H be the upper half-plane; let Γ be a Fuchsian group; let M=H\Γ be a Riemann surface of negative curvature, and let T1M be the tangent bundle of unit-length vectors on the manifold M, and let T1H be the tangent bundle of unit-length vectors on H. Note that a bundle of unit-length vectors on a surface is the principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
of a complex line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
.
Lie vector fields
One starts by noting that T1H is isomorphic to the Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
PSL(2,R). This group is the group of orientation-preserving isometries of the upper half-plane. The Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of PSL(2,R) is sl(2,R), and is represented by the matrices
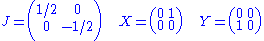
which have the algebra

The exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
s
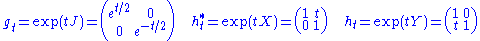
define right-invariant flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
s on the manifold of T1H=PSL(2,R), and likewise on T1M. Defining P=T1H and Q=T1M, these flows define vector fields on P and Q, whose vectors lie in TP and TQ. These are just the standard, ordinary Lie vector fields on the manifold of a Lie group, and the presentation above is a standard exposition of a Lie vector field.
Anosov flow
The connection to the Anosov flow comes from the realization that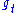 is the geodesic flow on P and Q. Lie vector fields being (by definition) left invariant under the action of a group element, one has that these fields are left invariant under the specific elements
is the geodesic flow on P and Q. Lie vector fields being (by definition) left invariant under the action of a group element, one has that these fields are left invariant under the specific elements 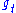 of the geodesic flow. In other words, the spaces TP and TQ are split into three one-dimensional spaces, or subbundle
of the geodesic flow. In other words, the spaces TP and TQ are split into three one-dimensional spaces, or subbundleSubbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
s, each of which are invariant under the geodesic flow. The final step is to notice that vector fields in one subbundle expand (and expand exponentially), those in another are unchanged, and those in a third shrink (and do so exponentially).
More precisely, the tangent bundle TQ may be written as the direct sum
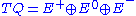
or, at a point
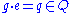 , the direct sum
, the direct sum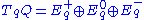
corresponding to the Lie algebra generators Y, J and X, respectively, carried, by the left action of group element g, from the origin e to the point q. That is, one has
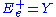 ,
, 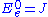 and
and 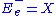 . These spaces are each subbundle
. These spaces are each subbundleSubbundle
In mathematics, a subbundle U of a vector bundle V on a topological space X is a collection of linear subspaces Ux of the fibers Vx of V at x in X, that make up a vector bundle in their own right....
s, and are preserved (are invariant) under the action of the geodesic flow; that is, under the action of group elements
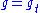 .
.To compare the lengths of vectors in
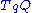 at different points q, one needs a metric. Any inner product at
at different points q, one needs a metric. Any inner product at 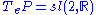 extends to a left-invariant Riemannian metric on P, and thus to a Riemannian metric on Q. The length of a vector
extends to a left-invariant Riemannian metric on P, and thus to a Riemannian metric on Q. The length of a vector 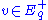 expands exponentially as exp(t) under the action of
expands exponentially as exp(t) under the action of 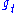 . The length of a vector
. The length of a vector 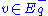 shrinks exponentially as exp(-t) under the action of
shrinks exponentially as exp(-t) under the action of 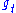 . Vectors in
. Vectors in 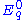 are unchanged. This may be seen by examining how the group elements commute. The geodesic flow is invariant,
are unchanged. This may be seen by examining how the group elements commute. The geodesic flow is invariant,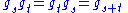
but the other two shrink and expand:

and

where we recall that a tangent vector in
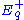 is given by the derivative
is given by the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
, with respect to t, of the curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
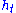 , the setting t=0.
, the setting t=0.Geometric interpretation of the Anosov flow
When acting on the point z=i of the upper half-plane,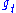 corresponds to a geodesic
corresponds to a geodesicGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
on the upper half plane, passing through the point z=i. The action is the standard Möbius transformation action of SL(2,R) on the upper half-plane, so that

A general geodesic is given by
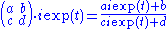
with a, b, c and d real, with ad-bc=1. The curves
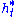 and
and 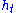 are called horocycles
are called horocyclesHorocycle
In hyperbolic geometry, a horocycle is a curve whose normals all converge asymptotically. It is the two-dimensional example of a horosphere ....
. Horocycles correspond to the motion of the normal vectors of a horosphere on the upper half-plane.

