Covering map
Encyclopedia
In mathematics
, more specifically algebraic topology
, a covering map is a continuous
surjective function
p from a topological space
, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p. This means that for each point x in X, there is associated an ordered pair
, (K, U), where U is a neighborhood of x and where K is a collection of disjoint open sets in C, each of which gets mapped homeomorphically
, via p, to U (as shown in the image). In particular, this means that every covering map is necessarily a local homeomorphism
. Under this definition, C is called a covering space of X.
Covering spaces play an important role in homotopy theory, harmonic analysis
, Riemannian geometry
and differential topology
. In Riemannian geometry for example, ramification is a generalization of the notion of covering maps. Covering spaces are also deeply intertwined with the study of homotopy groups and, in particular, the fundamental group
. An important application comes from the result that, if X is a "sufficiently good" topological space
, there is a bijection
from the collection of all isomorphism classes of connected coverings
of X and subgroups of the fundamental group
of X.
. A covering space of X is a space C together with a continuous surjective map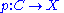
such that for every x ∈ X, there exists an open
neighborhood U of x, such that p−1(U) (the inverse image of U under p) is a disjoint union
of open sets in C, each of which is mapped homeomorphically
onto U by p.
The map p is called the covering map: the space X is often called the base space of the covering and the space C is called the total space of the covering. For any point x in the base the inverse image of x in C is necessarily a discrete space
called the fiber over x.
The special open neighborhoods U of x given in the definition are called evenly-covered neighborhoods. The evenly-covered neighborhoods form an open cover of the space X. The homeomorphic copies in C of an evenly-covered neighborhood U are called the sheets over U. One generally pictures C as "hovering above" X, with p mapping "downwards", the sheets over U being horizontally stacked above each other and above U, and the fiber over x consisting of those points of C that lie "vertically above" x. In particular, covering maps are locally trivial. This means that locally, each covering map is 'isomorphic' to a projection in the sense that there is a homeomorphism from the pre-image of an evenly covered neighbourhood U, to U X F, where F is the fiber, satisfying the local trivialization condition. That is, if we project this homeomorphism onto U (and thus the composition of the projection with this homeomorphism will be a map from the pre-image of U to U), the derived composition will equal p.
conditions on the spaces X and C in the definition of a covering map. In particular, many authors require both spaces to be path-connected and locally path-connected. This can prove helpful because many theorems hold only if the spaces in question have these properties. Some authors omit the assumption of surjectivity, for if X is connected and C is nonempty then surjectivity of the covering map actually follows from the other axioms.
S1 in R2. Then the map p : R → S1 with
is a cover where each point of S1 is covered infinitely often.
Consider the complex plane
with the origin removed, denoted by C×, and pick a non-zero integer
n. Then qn : C× → C× given by
is a cover. Here every fiber has n elements. The map qn leaves the unit circle S1 invariant and the restriction of this map to S1 is an n-fold cover of the circle by itself.
In fact, S1 and R are the only connected covering spaces of the circle. To prove this, we first note that the fundamental group of the circle is isomorphic to the additive group of integers Z. As follows from the correspondence between equivalence classes of connected coverings and conjugacy classes of subgroups of the fundamental group of the base space discussed below, a connected covering f : C →S1 is determined by a subgroup f#(π1(C)) of π1(S1) = Z, where f# is the induced homomorphism
. The group Z is abelian and it only has two kinds of subgroups: the trivial subgroup (which has infinite subgroup index
in Z) and the subgroups Hn = { kn | k ∈ Z } for n =1, 2, 3...., where Hn has index n in Z. Each of the subgroups Hn of Z is realized by the covering qn : S1 → S1 since one can check that (qn)# : Z → Z maps an integer k to kn and hence (qn)#(Z) = Hn. The trivial subgroup of Z is realized by the covering p : R → S1 since R is simply connected and has trivial fundamental group
and hence p#(π1(R)) = {0}, the trivial subgroup of Z. Since the total space of the coverings qn is S1 and since the total space of the covering p is R, this shows that every connected cover of S1 is either S1 or R.
A further example, originating from physics (see quantum mechanics
), is the special orthogonal group SO(3) of rotations of R3, which has the "double" covering group SU(2) of unitary rotations of C2 (in quantum mechanics acting as the group of spinor
rotations). Both groups have identical Lie algebra
s, but only SU(2) is simply connected
.
(i.e. to every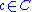
there exists an open set A in C containing c and an open set B in X such that the restriction of p to A yields a homeomorphism
between A and B). This implies that C and X share all local properties. If X is simply connected and C is connected, then this holds globally as well, and the covering p is a homeomorphism.
Homeomorphism of the fibres: For every x in X, the fiber over x is a discrete
subset of C. On every connected component
of X, the fibers are homeomorphic.
If X is connected, there is a discrete space F such that for every x in X the fiber over x is homeomorphic
to F and, moreover, for every x in X there is a neighborhood U of x such that its full pre-image p−1(U) is homeomorphic to U x F. In particular, the cardinality of the fiber over x is equal to the cardinality of F and it is called the degree of the cover p : C → X. Thus, if every fiber has n elements, we speak of an n-fold covering (for the case n = 1, the covering is trivial; when n = 2, the covering is a double cover; when n = 3, the covering is a triple cover and so on).
The lifting property: If p : C → X is a cover and γ is a path in X (i.e. a continuous map from the unit interval
[0,1] into X) and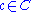
is a point "lying over" γ(0) (i.e. p(c) = γ(0)), then there exists a unique path Γ in C lying over γ (i.e. p o Γ = γ) and with Γ(0) = c. The curve Γ is called the lift of γ. If x and y are two points in X connected by a path, then that path furnishes a bijection
between the fiber over x and the fiber over y via the lifting property.
A more general lifting property is described as follows:
Let p : C → X be a cover and let f be a continuous map from Z to X where Z is path connected and locally path connected. Let z in Z be a base-point, let x = f(z) and let c in C be in the fiber over x, that is such that p(c)=x.
Then there exists a lift of f (that is, a continuous map g : Z → C such that p o g = f and g(z)=c) if and only if for the induced homomorphism
s at the level of the fundamental group
s we have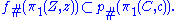
(♠)
Moreover, if such a lift g of f exists, it is unique.
In particular, if the space Z is assumed to be simply connected (so that π1(Z,z) = 1), condition (♠) is automatically satisfied and every continuous map from Z to X can be lifted. Since the unit interval [0,1] is simply connected, the lifting property for paths is a special case of the lifting property for maps stated above.
If p : C → X is a covering and c ∈ C and x ∈ X are such that p(c) = x, then the induced homomorphism
p# : π1(C,c) → π1(X,x) is injective and the induced homomorphisms p# : πn(C,c) → πn(X,x) are isomorphisms
for all n ≥ 2. Both of these statements can be deduced from the lifting property for continuous maps. Surjectivity of p# for n ≥ 2 follows from the fact that for n ≥ 2 the sphere Sn is simply connected and hence every continuous map from Sn to X can be lifted to C.
Equivalence: Let p1 : C1 → X and p2 : C2 → X be two coverings. One says that the two coverings p1 and p2 are equivalent if there exists a homeomorphism p21 : C2 → C1 and such that p2 = p1 o p21. Equivalence classes of coverings correspond to conjugacy classes of subgroups of the fundamental group
of X, as discussed below. If p21 : C2 → C1 is a covering (rather than a homeomorphism) and p2 = p1 o p21, then one says that p2 dominates p1.
Since coverings are local homeomorphism
s, a covering of a topological n-manifold
is an n-manifold. However a space covered by an n-manifold may be a non-Hausdorff manifold
. An example is given by letting C be the plane with the origin
deleted and X the quotient space obtained by identifying every point (x,y) with (2x, y/2). If p:C → X is the quotient map then it is a covering since the action of Z on C generated by f(x,y) = (2x,y/2) is properly discontinuous
. The points p(1,0) and p(0,1) do not have disjoint neighborhoods in X.
Any covering space of a differentiable manifold may be equipped with a (natural) differentiable structure that turns p (the covering map in question) into a local diffeomorphism
– a map with constant rank n.
cover comes from the following important property: if the mapping is a universal cover of the space and the mapping is any cover of the space where the covering space is connected, then there exists a covering map such that . This can be phrased as
The map is unique in the following sense: if we fix a point in the space and a point in the space with and a point in the space with , then there exists a unique covering map such that and .
If the space has a universal cover then that universal cover is essentially unique: if the mappings and are two universal covers of the space then there exists a homeomorphism such that .
The space has a universal cover if it is connected
, locally path-connected and semi-locally simply connected
. The universal cover of the space can be constructed as a certain space of paths in the space .
The example given above is a universal cover. The map from unit quaternions
to rotation
s of 3D space described in quaternions and spatial rotation
is also a universal cover.
If the space carries some additional structure, then its universal cover normally inherits that structure:
The universal cover first arose in the theory of analytic functions as the natural domain of an analytic continuation
.
acting
on the topological space
X. It is natural to ask under what conditions the projection,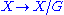
, from X to the orbit space, X/G, is a covering map. This is not always true since the action may have fixed points. An example for this is the cyclic group of order 2 acting on a product $Y \times Y$ by the twist action. Thus the study of the relation between the fundamental groups of X and X/G is not so straightforward. However the group G does act on the fundamental groupoid of X, and so the study is best handled by considering groups acting on groupoids, and the corresponding orbit groupoids. The theory for this is set down in Chapter 11 of the book Topology and groupoids referred to below.
f : C → C such that p o f = p. The set of all deck transformations of p forms a group under composition
, the deck transformation group Aut(p). Deck transformations are also called covering transformations. Every deck transformation permutes
the elements of each fiber. This defines a group action
of the deck transformation group on each fiber. Note that by the unique lifting property, if f is not the identity and C is path connected, then f has no fixed points
.
Now suppose p : C → X is a covering map and C (and therefore also X) is connected and locally path connected. The action of Aut(p) on each fiber is free
. If this action is transitive
on some fiber, then it is transitive on all fibers, and we call the cover regular. Every such regular cover is a principal G-bundle
, where G = Aut(p) is considered as a discrete topological group.
Every universal cover p : D → X is regular, with deck transformation group being isomorphic to the fundamental group
.
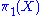The example p : C× → C× with p(z) = zn from above is a regular cover. The deck transformations are multiplications with n-th roots of unity
and the deck transformation group is therefore isomorphic to the cyclic group
Cn.
Another example: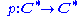
with 
from above is regular. Here one has a hierarchy of deck transformation groups. In fact Cx! is a subgroup of Cy!, for 
.
in C with starting point c. The end point of this lifted path need not be c, but it must lie in the fiber over x. It turns out that this end point only depends on the class of γ in the fundamental group
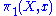, and in this fashion we obtain a right group action
of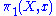
on the fiber over x. This is known as the monodromy
action.
So there are two actions on the fiber over x: Aut(p) acts on the left and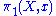
acts on the right. These two actions are compatible in the following sense:
for all f in Aut(p), c in p -1(x) and γ in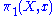
.
If p is a universal cover, then Aut(p) can be naturally identified with the opposite
group of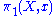
so that the left action of the opposite group of 
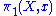coincides with the action of Aut(p) on the fiber over x. Note that Aut(p) and 
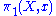are naturally isomorphic in this case (as a group is always naturally isomorphic to its opposite through 
).
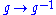If p is a regular cover, then Aut(p) is naturally isomorphic to a quotient of
.
In general (for good spaces), Aut(p) is naturally isomorphic to the quotient of the normalizer
of
in 
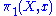over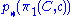 
, where 
.
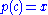There is an induced homomorphism
of fundamental group
s p# : π1(C,c) → π1(X,x) which is injective by the lifting property of coverings. Specifically if γ is a closed loop at c such that p#([γ]) = 1, that is p o γ is null-homotopic in X, then consider a null-homotopy of p o γ as a map f : D2 → X from the 2-disc D2 to X such that the restriction of f to the boundary S1 of D2 is equal to p o γ. By the lifting property the map f lifts to a continuous map g : D2 → C such that the restriction of f to the boundary S1 of D2 is equal to γ. Therefore γ is null-homotopic in C, so that the kernel
of p# : π1(C,c) → π1(X,x) is trivial and thus p# : π1(C,c) → π1(X,x) is an injective homomorphism.
Therefore π1(C,c) is isomorphic to the subgroup p# (π1(C,c)) of π1(X,x). If c1 ∈ C is another pre-image of x in C then the subgroup
s p# (π1(C,c)) and p# (π1(C,c1)) are conjugate
in π1(X,x) by p-image of a curve in C connecting c to c1. Thus a covering map p : C → X defines a conjugacy class of subgroups of π1(X,x) and one can show that equivalent covers of X define the same conjugacy class of subgroups of π1(X,x).
For a covering p : C → X the group p#(π1(C,c)) can also be seen to be equal to
,
the set of homotopy classes of those closed curves γ based at x whose lifts γC in C, starting at c, are closed curves at c. If X and C are path-connected, the degree of the cover p (that is, the cardinality of any fiber of p) is equal to the index
[π1(X,x):p# (π1(C,c))] of the subgroup
p# (π1(C,c)) in π1(X,x).
A key result of the covering space theory says that for a "sufficiently good" space X (namely, if X is path-connected, locally path-connected and semi-locally simply connected
) there is in fact a bijection between equivalence classes of path-connected covers of X and the conjugacy classes of subgroups of the fundamental group π1(X,x). The main step in proving this result is establishing the existence of a universal cover, that is a cover corresponding to the trivial subgroup of π1(X,x). Once the existence of a universal cover C of X is established, if H ≤ π1(X,x) is an arbitrary subgroup, the space C/H is the covering of X corresponding to H. One also needs to check that two covers of C corresponding to the same (conjugacy class of) subgroup of π1(X,x) are equivalent. Connected cell complexes and connected manifold
s are examples of "sufficiently good" spaces.
Let N(Γp) be the normalizer of Γp in π1(X,x). The deck transformation group Aut(p) is isomorphic to the quotient group
N(Γp)/Γp. If p is a universal covering, then Γp is the trivial group
, and Aut(p) is isomorphic to π1(X).
Let us reverse this argument. Let N be a normal subgroup
of π1(X,x). By the above arguments, this defines a (regular) covering p : C → X . Let c1 in C be in the fiber of x. Then for every other c2 in the fiber of x, there is precisely one deck transformation that takes c1 to c2. This deck transformation corresponds to a curve g in C connecting c1 to c2.
. Thus a particular kind of map of spaces is well modelled by a particular kind of morphism of groupoids. The category of covering morphisms of a groupoid G is also equivalent to the category of actions of G on sets, and this allows the recovery of more traditional classifications of coverings. Proofs of these facts are given in the book `Topology and Groupoids' referenced below.
s πn(X) =0 for all n ≥ 2, then the universal covering space T of X is contractible, as follows from applying the Whitehead theorem
to T. In this case X is a classifying space
or K(G,1) for G = π1(X).
Moreover, for every n ≥ 0 the group of cellular n-chains Cn(T) (that is, a free abelian group
with basis given by n-cells in T) also has a natural ZG-module
structure. Here for an n-cell σ in T and for g in G the cell g σ is exactly the translate of σ by a covering transformation of T corresponding to g. Moreover, Cn(T) is a free
ZG-module with free ZG-basis given by representatives of G-orbits of n-cells in T. In this case the standard topological chain complex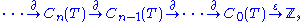
where ε is the augmentation map, is a free ZG-resolution of Z (where Z is equipped with the trivial ZG-module structure, g m = m for every g ∈ G and every m ∈ Z).
This resolution can be used to compute group cohomology
of G with arbitrary coefficients.
whose topology is not discrete, difficulties arise. Some progress has been made for more complex spaces, such as the Hawaiian earring
; see the references there for further information.
An important practical application of covering spaces occurs in charts on SO(3)
, the rotation group
. This group occurs widely in engineering, due to 3-dimensional rotations being heavily used in navigation
, nautical engineering, and aerospace engineering
, among many other uses. Topologically, SO(3) is the real projective space
RP3, with fundamental group Z/2, and only (non-trivial) covering space the hypersphere S3, which is the group Spin(3), and represented by the unit quaternions. Thus quaternions are a preferred method for representing spatial rotations – see quaternions and spatial rotation
.
However, it is often desirable to represent rotations by a set of three numbers, known as Euler angles
(in numerous variants), both because this is conceptually simpler, and because one can build a combination of three gimbal
s to produce rotations in three dimensions. Topologically this corresponds to a map from the 3-torus T3 of three angles to the real projective space RP3 of rotations, and the resulting map has imperfections due to this map being unable to be a covering map. Specifically, the failure of the map to be a local homeomorphism at certain points is referred to as gimbal lock
, and is demonstrated in the animation at the right – at some points (when the axes are coplanar) the rank of the map is 2, rather than 3, meaning that only 2 dimensions of rotations can be realized from that point by changing the angles. This causes problems in applications, and is formalized by the notion of a covering space.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a covering map is a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
surjective function
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
p from a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p. This means that for each point x in X, there is associated an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
, (K, U), where U is a neighborhood of x and where K is a collection of disjoint open sets in C, each of which gets mapped homeomorphically
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
, via p, to U (as shown in the image). In particular, this means that every covering map is necessarily a local homeomorphism
Local homeomorphism
In mathematics, more specifically topology, a local homeomorphism is intuitively a function, f, between topological spaces that preserves local structure. Equivalently, one can cover the domain of this function by open sets, such that f restricted to each such open set is a homeomorphism onto its...
. Under this definition, C is called a covering space of X.
Covering spaces play an important role in homotopy theory, harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
. In Riemannian geometry for example, ramification is a generalization of the notion of covering maps. Covering spaces are also deeply intertwined with the study of homotopy groups and, in particular, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
. An important application comes from the result that, if X is a "sufficiently good" topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from the collection of all isomorphism classes of connected coverings
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of X and subgroups of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of X.
Formal definition
Let X be a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. A covering space of X is a space C together with a continuous surjective map
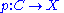
such that for every x ∈ X, there exists an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
neighborhood U of x, such that p−1(U) (the inverse image of U under p) is a disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of open sets in C, each of which is mapped homeomorphically
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
onto U by p.
The map p is called the covering map: the space X is often called the base space of the covering and the space C is called the total space of the covering. For any point x in the base the inverse image of x in C is necessarily a discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
called the fiber over x.
The special open neighborhoods U of x given in the definition are called evenly-covered neighborhoods. The evenly-covered neighborhoods form an open cover of the space X. The homeomorphic copies in C of an evenly-covered neighborhood U are called the sheets over U. One generally pictures C as "hovering above" X, with p mapping "downwards", the sheets over U being horizontally stacked above each other and above U, and the fiber over x consisting of those points of C that lie "vertically above" x. In particular, covering maps are locally trivial. This means that locally, each covering map is 'isomorphic' to a projection in the sense that there is a homeomorphism from the pre-image of an evenly covered neighbourhood U, to U X F, where F is the fiber, satisfying the local trivialization condition. That is, if we project this homeomorphism onto U (and thus the composition of the projection with this homeomorphism will be a map from the pre-image of U to U), the derived composition will equal p.
Alternative definitions
Many authors impose some connectivityConnectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
conditions on the spaces X and C in the definition of a covering map. In particular, many authors require both spaces to be path-connected and locally path-connected. This can prove helpful because many theorems hold only if the spaces in question have these properties. Some authors omit the assumption of surjectivity, for if X is connected and C is nonempty then surjectivity of the covering map actually follows from the other axioms.
Examples
Consider the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
S1 in R2. Then the map p : R → S1 with
- p(t) = (cos(t),sin(t))
is a cover where each point of S1 is covered infinitely often.
Consider the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
with the origin removed, denoted by C×, and pick a non-zero integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n. Then qn : C× → C× given by
- qn(z) = zn
is a cover. Here every fiber has n elements. The map qn leaves the unit circle S1 invariant and the restriction of this map to S1 is an n-fold cover of the circle by itself.
In fact, S1 and R are the only connected covering spaces of the circle. To prove this, we first note that the fundamental group of the circle is isomorphic to the additive group of integers Z. As follows from the correspondence between equivalence classes of connected coverings and conjugacy classes of subgroups of the fundamental group of the base space discussed below, a connected covering f : C →S1 is determined by a subgroup f#(π1(C)) of π1(S1) = Z, where f# is the induced homomorphism
Induced homomorphism
In mathematics, an induced homomorphism is a structure-preserving map between a pair of objects that is derived in a canonical way from another map between another pair of objects. A particularly important case arises in algebraic topology, where any continuous function between two pointed...
. The group Z is abelian and it only has two kinds of subgroups: the trivial subgroup (which has infinite subgroup index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
in Z) and the subgroups Hn = { kn | k ∈ Z } for n =1, 2, 3...., where Hn has index n in Z. Each of the subgroups Hn of Z is realized by the covering qn : S1 → S1 since one can check that (qn)# : Z → Z maps an integer k to kn and hence (qn)#(Z) = Hn. The trivial subgroup of Z is realized by the covering p : R → S1 since R is simply connected and has trivial fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
and hence p#(π1(R)) = {0}, the trivial subgroup of Z. Since the total space of the coverings qn is S1 and since the total space of the covering p is R, this shows that every connected cover of S1 is either S1 or R.
A further example, originating from physics (see quantum mechanics
Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
), is the special orthogonal group SO(3) of rotations of R3, which has the "double" covering group SU(2) of unitary rotations of C2 (in quantum mechanics acting as the group of spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
rotations). Both groups have identical Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, but only SU(2) is simply connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
.
Properties
Common local properties: Every cover p : C → X is a local homeomorphismLocal homeomorphism
In mathematics, more specifically topology, a local homeomorphism is intuitively a function, f, between topological spaces that preserves local structure. Equivalently, one can cover the domain of this function by open sets, such that f restricted to each such open set is a homeomorphism onto its...
(i.e. to every
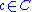there exists an open set A in C containing c and an open set B in X such that the restriction of p to A yields a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
between A and B). This implies that C and X share all local properties. If X is simply connected and C is connected, then this holds globally as well, and the covering p is a homeomorphism.
Homeomorphism of the fibres: For every x in X, the fiber over x is a discrete
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
subset of C. On every connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of X, the fibers are homeomorphic.
If X is connected, there is a discrete space F such that for every x in X the fiber over x is homeomorphic
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to F and, moreover, for every x in X there is a neighborhood U of x such that its full pre-image p−1(U) is homeomorphic to U x F. In particular, the cardinality of the fiber over x is equal to the cardinality of F and it is called the degree of the cover p : C → X. Thus, if every fiber has n elements, we speak of an n-fold covering (for the case n = 1, the covering is trivial; when n = 2, the covering is a double cover; when n = 3, the covering is a triple cover and so on).
The lifting property: If p : C → X is a cover and γ is a path in X (i.e. a continuous map from the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1] into X) and
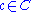is a point "lying over" γ(0) (i.e. p(c) = γ(0)), then there exists a unique path Γ in C lying over γ (i.e. p o Γ = γ) and with Γ(0) = c. The curve Γ is called the lift of γ. If x and y are two points in X connected by a path, then that path furnishes a bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between the fiber over x and the fiber over y via the lifting property.
A more general lifting property is described as follows:
Let p : C → X be a cover and let f be a continuous map from Z to X where Z is path connected and locally path connected. Let z in Z be a base-point, let x = f(z) and let c in C be in the fiber over x, that is such that p(c)=x.
Then there exists a lift of f (that is, a continuous map g : Z → C such that p o g = f and g(z)=c) if and only if for the induced homomorphism
Induced homomorphism
In mathematics, an induced homomorphism is a structure-preserving map between a pair of objects that is derived in a canonical way from another map between another pair of objects. A particularly important case arises in algebraic topology, where any continuous function between two pointed...
s at the level of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s we have
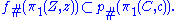(♠)Moreover, if such a lift g of f exists, it is unique.
In particular, if the space Z is assumed to be simply connected (so that π1(Z,z) = 1), condition (♠) is automatically satisfied and every continuous map from Z to X can be lifted. Since the unit interval [0,1] is simply connected, the lifting property for paths is a special case of the lifting property for maps stated above.
If p : C → X is a covering and c ∈ C and x ∈ X are such that p(c) = x, then the induced homomorphism
Induced homomorphism
In mathematics, an induced homomorphism is a structure-preserving map between a pair of objects that is derived in a canonical way from another map between another pair of objects. A particularly important case arises in algebraic topology, where any continuous function between two pointed...
p# : π1(C,c) → π1(X,x) is injective and the induced homomorphisms p# : πn(C,c) → πn(X,x) are isomorphisms
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
for all n ≥ 2. Both of these statements can be deduced from the lifting property for continuous maps. Surjectivity of p# for n ≥ 2 follows from the fact that for n ≥ 2 the sphere Sn is simply connected and hence every continuous map from Sn to X can be lifted to C.
Equivalence: Let p1 : C1 → X and p2 : C2 → X be two coverings. One says that the two coverings p1 and p2 are equivalent if there exists a homeomorphism p21 : C2 → C1 and such that p2 = p1 o p21. Equivalence classes of coverings correspond to conjugacy classes of subgroups of the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of X, as discussed below. If p21 : C2 → C1 is a covering (rather than a homeomorphism) and p2 = p1 o p21, then one says that p2 dominates p1.
Since coverings are local homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s, a covering of a topological n-manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is an n-manifold. However a space covered by an n-manifold may be a non-Hausdorff manifold
Non-Hausdorff manifold
In mathematics, it is a usual axiom of a manifold to be a Hausdorff space, and this is assumed throughout geometry and topology: "manifold" means " Hausdorff manifold"....
. An example is given by letting C be the plane with the origin
deleted and X the quotient space obtained by identifying every point (x,y) with (2x, y/2). If p:C → X is the quotient map then it is a covering since the action of Z on C generated by f(x,y) = (2x,y/2) is properly discontinuous
Properly discontinuous
In topology and related branches of mathematics, an action of a group G on a topological space X is called proper if the map from G×X to X×X taking to is proper, and is called properly discontinuous if in addition G is discrete...
. The points p(1,0) and p(0,1) do not have disjoint neighborhoods in X.
Any covering space of a differentiable manifold may be equipped with a (natural) differentiable structure that turns p (the covering map in question) into a local diffeomorphism
Local diffeomorphism
In mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
– a map with constant rank n.
Universal covers
A connected covering space is a universal cover if it is simply connected. The name universalUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
cover comes from the following important property: if the mapping is a universal cover of the space and the mapping is any cover of the space where the covering space is connected, then there exists a covering map such that . This can be phrased as
The universal cover of the space covers all connected covers of the space .
The map is unique in the following sense: if we fix a point in the space and a point in the space with and a point in the space with , then there exists a unique covering map such that and .
If the space has a universal cover then that universal cover is essentially unique: if the mappings and are two universal covers of the space then there exists a homeomorphism such that .
The space has a universal cover if it is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, locally path-connected and semi-locally simply connected
Semi-locally simply connected
In mathematics, specifically algebraic topology, the phrase semi-locally simply connected refers to a certain local connectedness condition that arises in the theory of covering spaces. Roughly speaking, a topological space X is semi-locally simply connected if there is a lower bound on the sizes...
. The universal cover of the space can be constructed as a certain space of paths in the space .
The example given above is a universal cover. The map from unit quaternions
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
to rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s of 3D space described in quaternions and spatial rotation
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
is also a universal cover.
If the space carries some additional structure, then its universal cover normally inherits that structure:
- if the space is a manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, then so is its universal cover - if the space is a Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, then so is its universal cover , and is a holomorphic map - if the space is a Lorentzian manifold, then so is its universal cover. Furthermore, suppose the subset is a disjoint unionDisjoint unionIn mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of open sets each of which is diffeomorphic with by the mapping . If the space contains a closed timelike curveClosed timelike curveIn mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
, then the space is timelike multiply connected (no CTC can be timelike homotopic to a point, as that point would not be causally well-behaved), its universal (diffeomorphic) cover is timelike simply connectedTimelike simply connectedSuppose a Lorentzian manifold contains a closed timelike curve . No CTC can be continuously deformed as a CTC to a point, as that point would not be causally well behaved. Therefore, any Lorentzian manifold containing a CTC is said to be timelike multiply connected...
(it does not contain a CTC). - if is a Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
(as in the two examples above), then so is its universal cover , and the mapping is a homomorphism of Lie groups. In this case the universal cover is also called the universal covering groupUniversal covering groupIn mathematics, a covering group of a topological group H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism. The map p is called the covering homomorphism...
. This has particular application to representation theoryRepresentation theoryRepresentation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
and quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, since ordinary representationsGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the universal covering group are projective representationProjective representationIn the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s of the original (classical) group .
The universal cover first arose in the theory of analytic functions as the natural domain of an analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
.
G-coverings
Let G be a discrete groupDiscrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on the topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X. It is natural to ask under what conditions the projection,
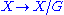, from X to the orbit space, X/G, is a covering map. This is not always true since the action may have fixed points. An example for this is the cyclic group of order 2 acting on a product $Y \times Y$ by the twist action. Thus the study of the relation between the fundamental groups of X and X/G is not so straightforward. However the group G does act on the fundamental groupoid of X, and so the study is best handled by considering groups acting on groupoids, and the corresponding orbit groupoids. The theory for this is set down in Chapter 11 of the book Topology and groupoids referred to below.Deck transformation group, regular covers
A deck transformation or automorphism of a cover p : C → X is a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
f : C → C such that p o f = p. The set of all deck transformations of p forms a group under composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, the deck transformation group Aut(p). Deck transformations are also called covering transformations. Every deck transformation permutes
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
the elements of each fiber. This defines a group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the deck transformation group on each fiber. Note that by the unique lifting property, if f is not the identity and C is path connected, then f has no fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
Now suppose p : C → X is a covering map and C (and therefore also X) is connected and locally path connected. The action of Aut(p) on each fiber is free
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. If this action is transitive
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on some fiber, then it is transitive on all fibers, and we call the cover regular. Every such regular cover is a principal G-bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
, where G = Aut(p) is considered as a discrete topological group.
Every universal cover p : D → X is regular, with deck transformation group being isomorphic to the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
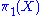.The example p : C× → C× with p(z) = zn from above is a regular cover. The deck transformations are multiplications with n-th roots of unity
Root of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
and the deck transformation group is therefore isomorphic to the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Cn.
Another example:
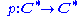with from above is regular. Here one has a hierarchy of deck transformation groups. In fact Cx! is a subgroup of Cy!, for .Monodromy action
Again suppose p : C → X is a covering map and C (and therefore also X) is connected and locally path connected. If x is in X and c belongs to the fiber over x (i.e. p(c) = x), and γ:[0,1]→X is a path with γ(0)=γ(1)=x, then this path lifts to a unique pathHomotopy lifting property
In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...
in C with starting point c. The end point of this lifted path need not be c, but it must lie in the fiber over x. It turns out that this end point only depends on the class of γ in the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
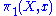, and in this fashion we obtain a right group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of
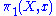on the fiber over x. This is known as the monodromyMonodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
action.
So there are two actions on the fiber over x: Aut(p) acts on the left and
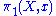acts on the right. These two actions are compatible in the following sense:
- f.(c.γ) = (f.c).γ
for all f in Aut(p), c in p -1(x) and γ in
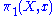.If p is a universal cover, then Aut(p) can be naturally identified with the opposite
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
group of
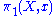so that the left action of the opposite group of 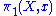coincides with the action of Aut(p) on the fiber over x. Note that Aut(p) and 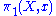are naturally isomorphic in this case (as a group is always naturally isomorphic to its opposite through 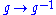).If p is a regular cover, then Aut(p) is naturally isomorphic to a quotient of
.In general (for good spaces), Aut(p) is naturally isomorphic to the quotient of the normalizer
Centralizer and normalizer
In group theory, the centralizer and normalizer of a subset S of a group G are subgroups of G which have a restricted action on the elements of S and S as a whole, respectively...
of
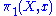in over 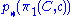, where 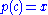.More on the group structure
Let p : C → X be a covering map where both X and C are path-connected. Let x ∈ X be a basepoint of X and let c ∈ C be one of its pre-images in C, that is p(c) = x.There is an induced homomorphism
Induced homomorphism
In mathematics, an induced homomorphism is a structure-preserving map between a pair of objects that is derived in a canonical way from another map between another pair of objects. A particularly important case arises in algebraic topology, where any continuous function between two pointed...
of fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s p# : π1(C,c) → π1(X,x) which is injective by the lifting property of coverings. Specifically if γ is a closed loop at c such that p#([γ]) = 1, that is p o γ is null-homotopic in X, then consider a null-homotopy of p o γ as a map f : D2 → X from the 2-disc D2 to X such that the restriction of f to the boundary S1 of D2 is equal to p o γ. By the lifting property the map f lifts to a continuous map g : D2 → C such that the restriction of f to the boundary S1 of D2 is equal to γ. Therefore γ is null-homotopic in C, so that the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of p# : π1(C,c) → π1(X,x) is trivial and thus p# : π1(C,c) → π1(X,x) is an injective homomorphism.
Therefore π1(C,c) is isomorphic to the subgroup p# (π1(C,c)) of π1(X,x). If c1 ∈ C is another pre-image of x in C then the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s p# (π1(C,c)) and p# (π1(C,c1)) are conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
in π1(X,x) by p-image of a curve in C connecting c to c1. Thus a covering map p : C → X defines a conjugacy class of subgroups of π1(X,x) and one can show that equivalent covers of X define the same conjugacy class of subgroups of π1(X,x).
For a covering p : C → X the group p#(π1(C,c)) can also be seen to be equal to
,the set of homotopy classes of those closed curves γ based at x whose lifts γC in C, starting at c, are closed curves at c. If X and C are path-connected, the degree of the cover p (that is, the cardinality of any fiber of p) is equal to the index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
[π1(X,x):p# (π1(C,c))] of the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
p# (π1(C,c)) in π1(X,x).
A key result of the covering space theory says that for a "sufficiently good" space X (namely, if X is path-connected, locally path-connected and semi-locally simply connected
Semi-locally simply connected
In mathematics, specifically algebraic topology, the phrase semi-locally simply connected refers to a certain local connectedness condition that arises in the theory of covering spaces. Roughly speaking, a topological space X is semi-locally simply connected if there is a lower bound on the sizes...
) there is in fact a bijection between equivalence classes of path-connected covers of X and the conjugacy classes of subgroups of the fundamental group π1(X,x). The main step in proving this result is establishing the existence of a universal cover, that is a cover corresponding to the trivial subgroup of π1(X,x). Once the existence of a universal cover C of X is established, if H ≤ π1(X,x) is an arbitrary subgroup, the space C/H is the covering of X corresponding to H. One also needs to check that two covers of C corresponding to the same (conjugacy class of) subgroup of π1(X,x) are equivalent. Connected cell complexes and connected manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s are examples of "sufficiently good" spaces.
Let N(Γp) be the normalizer of Γp in π1(X,x). The deck transformation group Aut(p) is isomorphic to the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
N(Γp)/Γp. If p is a universal covering, then Γp is the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
, and Aut(p) is isomorphic to π1(X).
Let us reverse this argument. Let N be a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of π1(X,x). By the above arguments, this defines a (regular) covering p : C → X . Let c1 in C be in the fiber of x. Then for every other c2 in the fiber of x, there is precisely one deck transformation that takes c1 to c2. This deck transformation corresponds to a curve g in C connecting c1 to c2.
Relations with groupoids
One of the ways of expressing the algebraic content of the theory of covering spaces is using groupoids and the fundamental groupoid. The latter functor gives an equivalence of categories between the category of covering spaces of a reasonably nice space X and the category of groupoid covering morphisms of. Thus a particular kind of map of spaces is well modelled by a particular kind of morphism of groupoids. The category of covering morphisms of a groupoid G is also equivalent to the category of actions of G on sets, and this allows the recovery of more traditional classifications of coverings. Proofs of these facts are given in the book `Topology and Groupoids' referenced below.Relations with classifying spaces and group cohomology
If X is a connected cell complex with homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s πn(X) =0 for all n ≥ 2, then the universal covering space T of X is contractible, as follows from applying the Whitehead theorem
Whitehead theorem
In homotopy theory , the Whitehead theorem states that if a continuous mapping f between topological spaces X and Y induces isomorphisms on all homotopy groups, then f is a homotopy equivalence provided X and Y are connected and have the homotopy-type of CW complexes. This result was proved by J....
to T. In this case X is a classifying space
Classifying space
In mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
or K(G,1) for G = π1(X).
Moreover, for every n ≥ 0 the group of cellular n-chains Cn(T) (that is, a free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
with basis given by n-cells in T) also has a natural ZG-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
structure. Here for an n-cell σ in T and for g in G the cell g σ is exactly the translate of σ by a covering transformation of T corresponding to g. Moreover, Cn(T) is a free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
ZG-module with free ZG-basis given by representatives of G-orbits of n-cells in T. In this case the standard topological chain complex
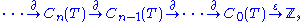
where ε is the augmentation map, is a free ZG-resolution of Z (where Z is equipped with the trivial ZG-module structure, g m = m for every g ∈ G and every m ∈ Z).
This resolution can be used to compute group cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
of G with arbitrary coefficients.
Generalizations
As a homotopy theory, the notion of covering spaces works well when the deck transformation group is discrete, or, equivalently, when the space is locally path-connected. However, when the deck transformation group is a topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
whose topology is not discrete, difficulties arise. Some progress has been made for more complex spaces, such as the Hawaiian earring
Hawaiian earring
In mathematics, the Hawaiian earring H is the topological space defined by the union of circles in the Euclidean plane R2 with center and radius 1/n for n = 1, 2, 3, ......
; see the references there for further information.
Applications
Charts on SO(3)
In mathematics, the special orthogonal group in three dimensions, otherwise known as the rotation group SO, is a naturally occurring example of a manifold. The various charts on SO set up rival coordinate systems: in this case there cannot be said to be a preferred set of parameters describing a...
, the rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
. This group occurs widely in engineering, due to 3-dimensional rotations being heavily used in navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
, nautical engineering, and aerospace engineering
Aerospace engineering
Aerospace engineering is the primary branch of engineering concerned with the design, construction and science of aircraft and spacecraft. It is divided into two major and overlapping branches: aeronautical engineering and astronautical engineering...
, among many other uses. Topologically, SO(3) is the real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
RP3, with fundamental group Z/2, and only (non-trivial) covering space the hypersphere S3, which is the group Spin(3), and represented by the unit quaternions. Thus quaternions are a preferred method for representing spatial rotations – see quaternions and spatial rotation
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
.
However, it is often desirable to represent rotations by a set of three numbers, known as Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
(in numerous variants), both because this is conceptually simpler, and because one can build a combination of three gimbal
Gimbal
A gimbal is a pivoted support that allows the rotation of an object about a single axis. A set of two gimbals, one mounted on the other with pivot axes orthogonal, may be used to allow an object mounted on the innermost gimbal to remain immobile regardless of the motion of its support...
s to produce rotations in three dimensions. Topologically this corresponds to a map from the 3-torus T3 of three angles to the real projective space RP3 of rotations, and the resulting map has imperfections due to this map being unable to be a covering map. Specifically, the failure of the map to be a local homeomorphism at certain points is referred to as gimbal lock
Gimbal lock
Gimbal lock is the loss of one degree of freedom in a three-dimensional space that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space....
, and is demonstrated in the animation at the right – at some points (when the axes are coplanar) the rank of the map is 2, rather than 3, meaning that only 2 dimensions of rotations can be realized from that point by changing the angles. This causes problems in applications, and is formalized by the notion of a covering space.
See also
- Bethe latticeBethe latticeA Bethe lattice or Cayley tree , introduced by Hans Bethe in 1935, is a connected cycle-free graph where each node is connected to z neighbours, where z is called the coordination number. It can be seen as a tree-like structure emanating from a central node, with all the nodes arranged in shells...
is the universal cover of a Cayley graphCayley graphIn mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group... - Covering graphCovering graphIn the mathematical discipline of graph theory, a graph C is a covering graph of another graph G if there is a covering map from the vertex set of C to the vertex set of G...
, a covering space for an undirected graph, and its special case the bipartite double coverBipartite double coverIn graph theoretic mathematics, the bipartite double cover of an undirected graph G is a bipartite covering graph of G, with twice as many vertices as G. It can be constructed as the tensor product of graphs G × K2...
. - Covering group
- Galois connectionGalois connectionIn mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...