Homotopy group
Encyclopedia
In mathematics
, homotopy groups are used in algebraic topology
to classify topological space
s. The first and simplest homotopy group is the fundamental group
, which records information about loop
s in a space
. Intuitively, homotopy groups record information about the basic shape, or holes, of a topological space.
To define the n-th homotopy group, the base point preserving maps from an n-dimensional sphere
(with base point) into a given space (with base point) are collected into equivalence classes, called homotopy classes. Two mappings are homotopic if one can be continuously deformed into the other. These homotopy classes form a group
, called the n-th homotopy group, πn(X), of the given space X with base point. Topological spaces with differing homotopy groups are never equivalent (homeomorphic), but the converse is not true.
The notion of homotopy of path
s was introduced by Camille Jordan
.
by associating
to every object of this category a simpler object which still retains a sufficient amount of information about the object in question. Homotopy groups are a certain way of associating groups to topological spaces. A group
is a set which allows adding of elements in a suitable sense. For example, the integers Z form a group. Another example are the finite groups Z/sZ
.
The provided link between topology and groups allows the application of group theory
to get insights in topology
. For example, if two topological objects have different homotopy groups, they can't have the same topological structure, a fact which may be difficult to prove without resorting to non-topological means. For example, the torus
seems to be visibly different from the sphere
, the former having a "hole", the latter one not having one. However, as continuity, the basic notion of topology, only deals with the local structure, it can be difficult to formally pin down this intuition. The homotopy groups, however, carry information about the global structure.
As for the example: one can show that the first homotopy group of the torus T is
because the universal cover of the torus is the complex plane C, mapping to the torus T ≅ C / Z2. On the other hand the sphere S2 satisfies
because every loop can be contracted to a constant map (see homotopy groups of spheres
for this and more complicated examples of homotopy groups).
Hence the torus is not homeomorphic to the sphere.
Sn we choose a base point a. For a space X with base point b, we define πn(X) to be the set of homotopy classes of maps
that map the base point a to the base point b. In particular, the equivalence classes are given by homotopies that are constant on the basepoint of the sphere. Equivalently, we can define πn(X) to be the group of homotopy classes of maps g : [0,1]n → X from the n-cube
to X that take the boundary of the n-cube to b.
For n ≥ 1, the homotopy classes form a group
. To define the group operation, recall that in the fundamental group
, the product f * g of two loops f and g is defined by setting (f * g)(t) = f(2t) if t is in [0,1/2] and (f * g)(t) = g(2t − 1) if t is in [1/2,1]. The idea of composition in the fundamental group is that of following the first path and the second in succession, or, equivalently, setting their two domains together. The concept of composition that we want for the n-th homotopy group is the same, except that now the domains that we stick together are cubes, and we must glue them along a face. We therefore define the sum of maps f, g : [0,1]n → X by the formula (f + g)(t1, t2, ... tn) = f(2t1, t2, ... tn) for t1 in [0,1/2] and (f + g)(t1, t2, ... tn) = g(2t1 − 1, t2, ... tn) for t1 in [1/2,1]. For the corresponding definition in terms of spheres, define the sum f + g of maps f, g : Sn → X to be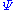
composed with h, where 
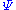is the map from Sn to the wedge sum
of two n-spheres that collapses the equator and h is the map from the wedge sum of two n-spheres to X that is defined to be f on the first sphere and g on the second.
If n ≥ 2, then πn is abelian
. (For a proof of this, note that in two dimensions or greater, two homotopies can be "rotated" around each other. See Eckmann–Hilton argument)
It is tempting to try to simplify the definition of homotopy groups by omitting the base points, but this does not usually work for spaces that are not simply connected
, even for path connected spaces. The set of homotopy classes of maps from a sphere to a path connected space is not the homotopy group, but is essentially the set of orbits of the fundamental group on the homotopy group, and in general has no natural group structure.
A way out of these difficulties has been found by defining higher homotopy groupoids of filtered spaces and of n-cubes of spaces. These are related to relative homotopy groups and to n-adic homotopy groups respectively. A higher homotopy van Kampen theorem then enables one to derive some new information on homotopy groups and even on homotopy types. For more background and references, see "Higher dimensional group theory" and the references below.
with respect to CW complex
es. Suppose that B is path-connected. Then there is a long exact sequence
of homotopy groups
Here the maps involving π0 are not group homomorphism
s because the π0 are not groups, but they are exact in the sense that the image equals the kernel.
Example: the Hopf fibration. Let B equal S2 and E equal S3. Let p be the Hopf fibration, which has fiber S1. From the long exact sequence
and the fact that πn(S1) = 0 for n ≥ 2, we find that πn(S3) = πn(S2) for n ≥ 3. In particular, π3(S2) = π3(S3) = Z.
In the case of a cover space, when the fiber is discrete, we have that πn(E) is isomorphic to πn(B) for all n greater than 1, that πn(E) embeds injectively into πn(B) for all positive n, and that the subgroup of π1(B) that corresponds to the embedding of π1(E) has cosets in bijection with the elements of the fiber.
learned in algebraic topology. Unlike the Seifert–van Kampen theorem
for the fundamental group and the Excision theorem
for singular homology
and cohomology
, there is no simple way to calculate the homotopy groups of a space by breaking it up into smaller spaces. However methods developed in the 1980s involving a van Kampen type theorem for higher homotopy groupoids have allowed new calculations on homotopy types and so on homotopy groups. See for a sample result the 2008 paper by Ellis and Mikhailov listed below.
For some spaces, such as tori
, all higher homotopy groups (that is, second and higher homotopy groups) are trivial. These are the so-called aspherical space
s. However, despite intense research in calculating the homotopy groups of spheres, even in two dimensions a complete list is not known. To calculate even the fourth homotopy group of S2 one needs much more advanced techniques than the definitions might suggest. In particular the Serre spectral sequence
was constructed for just this purpose.
Certain Homotopy groups of n-connected
spaces can be calculated by comparison with homology groups via the Hurewicz theorem
.
There is a long exact sequence of relative homotopy groups.
. It is possible to define abstract homotopy groups for simplicial set
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, homotopy groups are used in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
to classify topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. The first and simplest homotopy group is the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, which records information about loop
Loop (topology)
In mathematics, a loop in a topological space X is a path f from the unit interval I = [0,1] to X such that f = f...
s in a space
Mathematical space
In mathematics, a space is a set with some added structure.Mathematical spaces often form a hierarchy, i.e., one space may inherit all the characteristics of a parent space...
. Intuitively, homotopy groups record information about the basic shape, or holes, of a topological space.
To define the n-th homotopy group, the base point preserving maps from an n-dimensional sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
(with base point) into a given space (with base point) are collected into equivalence classes, called homotopy classes. Two mappings are homotopic if one can be continuously deformed into the other. These homotopy classes form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, called the n-th homotopy group, πn(X), of the given space X with base point. Topological spaces with differing homotopy groups are never equivalent (homeomorphic), but the converse is not true.
The notion of homotopy of path
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
s was introduced by Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
.
Introduction
In modern mathematics it is common to study a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
by associating
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
to every object of this category a simpler object which still retains a sufficient amount of information about the object in question. Homotopy groups are a certain way of associating groups to topological spaces. A group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is a set which allows adding of elements in a suitable sense. For example, the integers Z form a group. Another example are the finite groups Z/sZ
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
.
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
to get insights in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. For example, if two topological objects have different homotopy groups, they can't have the same topological structure, a fact which may be difficult to prove without resorting to non-topological means. For example, the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
seems to be visibly different from the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, the former having a "hole", the latter one not having one. However, as continuity, the basic notion of topology, only deals with the local structure, it can be difficult to formally pin down this intuition. The homotopy groups, however, carry information about the global structure.
As for the example: one can show that the first homotopy group of the torus T is
- π1(T)=Z2,
because the universal cover of the torus is the complex plane C, mapping to the torus T ≅ C / Z2. On the other hand the sphere S2 satisfies
- π1(S2)=0,
because every loop can be contracted to a constant map (see homotopy groups of spheres
Homotopy groups of spheres
In the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
for this and more complicated examples of homotopy groups).
Hence the torus is not homeomorphic to the sphere.
Definition
In the n-sphereHypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
Sn we choose a base point a. For a space X with base point b, we define πn(X) to be the set of homotopy classes of maps
- f : Sn → X
that map the base point a to the base point b. In particular, the equivalence classes are given by homotopies that are constant on the basepoint of the sphere. Equivalently, we can define πn(X) to be the group of homotopy classes of maps g : [0,1]n → X from the n-cube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
to X that take the boundary of the n-cube to b.
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. To define the group operation, recall that in the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, the product f * g of two loops f and g is defined by setting (f * g)(t) = f(2t) if t is in [0,1/2] and (f * g)(t) = g(2t − 1) if t is in [1/2,1]. The idea of composition in the fundamental group is that of following the first path and the second in succession, or, equivalently, setting their two domains together. The concept of composition that we want for the n-th homotopy group is the same, except that now the domains that we stick together are cubes, and we must glue them along a face. We therefore define the sum of maps f, g : [0,1]n → X by the formula (f + g)(t1, t2, ... tn) = f(2t1, t2, ... tn) for t1 in [0,1/2] and (f + g)(t1, t2, ... tn) = g(2t1 − 1, t2, ... tn) for t1 in [1/2,1]. For the corresponding definition in terms of spheres, define the sum f + g of maps f, g : Sn → X to be
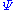composed with h, where 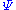is the map from Sn to the wedge sumWedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
of two n-spheres that collapses the equator and h is the map from the wedge sum of two n-spheres to X that is defined to be f on the first sphere and g on the second.
If n ≥ 2, then πn is abelian
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
. (For a proof of this, note that in two dimensions or greater, two homotopies can be "rotated" around each other. See Eckmann–Hilton argument)
It is tempting to try to simplify the definition of homotopy groups by omitting the base points, but this does not usually work for spaces that are not simply connected
Simply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
, even for path connected spaces. The set of homotopy classes of maps from a sphere to a path connected space is not the homotopy group, but is essentially the set of orbits of the fundamental group on the homotopy group, and in general has no natural group structure.
A way out of these difficulties has been found by defining higher homotopy groupoids of filtered spaces and of n-cubes of spaces. These are related to relative homotopy groups and to n-adic homotopy groups respectively. A higher homotopy van Kampen theorem then enables one to derive some new information on homotopy groups and even on homotopy types. For more background and references, see "Higher dimensional group theory" and the references below.
Long exact sequence of a fibration
Let p: E → B be a basepoint-preserving Serre fibration with fiber F, that is, a map possessing the homotopy lifting propertyHomotopy lifting property
In mathematics, in particular in homotopy theory within algebraic topology, the homotopy lifting property is a technical condition on a continuous function from a topological space E to another one, B...
with respect to CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
es. Suppose that B is path-connected. Then there is a long exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
of homotopy groups
- ... → πn(F) → πn(E) → πn(B) → πn−1(F) →... → π0(E) → 0.
Here the maps involving π0 are not group homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s because the π0 are not groups, but they are exact in the sense that the image equals the kernel.
Example: the Hopf fibration. Let B equal S2 and E equal S3. Let p be the Hopf fibration, which has fiber S1. From the long exact sequence
- ⋯ → πn(S1) → πn(S3) → πn(S2) → πn−1(S1) → ⋯
and the fact that πn(S1) = 0 for n ≥ 2, we find that πn(S3) = πn(S2) for n ≥ 3. In particular, π3(S2) = π3(S3) = Z.
In the case of a cover space, when the fiber is discrete, we have that πn(E) is isomorphic to πn(B) for all n greater than 1, that πn(E) embeds injectively into πn(B) for all positive n, and that the subgroup of π1(B) that corresponds to the embedding of π1(E) has cosets in bijection with the elements of the fiber.
Methods of calculation
Calculation of homotopy groups is in general much more difficult than some of the other homotopy invariantsInvariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
learned in algebraic topology. Unlike the Seifert–van Kampen theorem
Seifert–van Kampen theorem
In mathematics, the Seifert-van Kampen theorem of algebraic topology, sometimes just called van Kampen's theorem, expresses the structure of the fundamental group of a topological space X, in terms of the fundamental groups of two open, path-connected subspaces U and V that cover X...
for the fundamental group and the Excision theorem
Excision theorem
In algebraic topology, a branch of mathematics, the excision theorem is a useful theorem about relative homology—given topological spaces X and subspaces A and U such that U is also a subspace of A, the theorem says that under certain circumstances, we can cut out U from both spaces such...
for singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
and cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
, there is no simple way to calculate the homotopy groups of a space by breaking it up into smaller spaces. However methods developed in the 1980s involving a van Kampen type theorem for higher homotopy groupoids have allowed new calculations on homotopy types and so on homotopy groups. See for a sample result the 2008 paper by Ellis and Mikhailov listed below.
For some spaces, such as tori
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, all higher homotopy groups (that is, second and higher homotopy groups) are trivial. These are the so-called aspherical space
Aspherical space
In topology, a branch of mathematics, an aspherical space is a topological space with all higher homotopy groups equal to 0.If one works with CW complexes, one can reformulate this condition: an aspherical CW complex is a CW complex whose universal cover is contractible. Indeed, contractibility of...
s. However, despite intense research in calculating the homotopy groups of spheres, even in two dimensions a complete list is not known. To calculate even the fourth homotopy group of S2 one needs much more advanced techniques than the definitions might suggest. In particular the Serre spectral sequence
Serre spectral sequence
In mathematics, the Serre spectral sequence is an important tool in algebraic topology...
was constructed for just this purpose.
Certain Homotopy groups of n-connected
N-connected
In the mathematical branch of algebraic topology, specifically homotopy theory, n-connectedness is a way to say that a space vanishes or that a map is an isomorphism "up to dimension n, in homotopy".-n-connected space:...
spaces can be calculated by comparison with homology groups via the Hurewicz theorem
Hurewicz theorem
In mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism...
.
A list of methods for calculating homotopy groups
- The long exact sequence of homotopy groups of a fibration.
- Hurewicz theoremHurewicz theoremIn mathematics, the Hurewicz theorem is a basic result of algebraic topology, connecting homotopy theory with homology theory via a map known as the Hurewicz homomorphism...
, which has several versions. - Blakers–Massey theorem, also known as excision for homotopy groups.
- Freudenthal suspension theoremFreudenthal suspension theoremIn mathematics, and specifically in the field of homotopy theory, the Freudenthal suspension theorem is the fundamental result leading to the concept of stabilization of homotopy groups and ultimately to stable homotopy theory. It explains the behavior of simultaneously taking suspensions and...
, a corollary of excision for homotopy groups.
Relative homotopy groups
There are also relative homotopy groups πn(X,A) for a pair (X,A). The elements of such a group are homotopy classes of based maps Dn → X which carry the boundary Sn−1 into A. Two maps f, g are called homotopic relative to A if they are homotopic by a basepoint-preserving homotopy F : Dn × [0,1] → X such that, for each p in Sn−1 and t in [0,1], the element F(p,t) is in A. The ordinary homotopy groups are the special case in which A is the base point.There is a long exact sequence of relative homotopy groups.
Related notions
The homotopy groups are a cornerstone of the homotopy theory, which in turn stimulated the development of model categoriesModel category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
. It is possible to define abstract homotopy groups for simplicial set
Simplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
s.
See also
- Knot theoryKnot theoryIn topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
- Homotopy class
- Homotopy groups of spheresHomotopy groups of spheresIn the mathematical field of algebraic topology, the homotopy groups of spheres describe how spheres of various dimensions can wrap around each other. They are examples of topological invariants, which reflect, in algebraic terms, the structure of spheres viewed as topological spaces, forgetting...
- Topological invariant