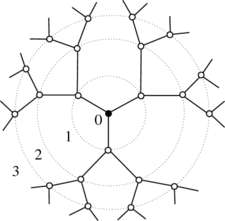
A Bethe lattice or Cayley tree (though the two are not completely equivalent, see below), introduced by Hans Bethe

Hans Bethe

Hans Albrecht Bethe was a German-American nuclear physicist, and Nobel laureate in physics for his work on the theory of stellar nucleosynthesis. A versatile theoretical physicist, Bethe also made important contributions to quantum electrodynamics, nuclear physics, solid-state physics and...

 in 1935, is a connected cycle-free graph

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

 where each node is connected to z neighbours, where z is called the coordination number

Coordination number

In chemistry and crystallography, the coordination number of a central atom in a molecule or crystal is the number of its nearest neighbours. This number is determined somewhat differently for molecules and for crystals....

. It can be seen as a tree-like structure emanating from a central node, with all the nodes arranged in shells around the central one. The central node may be called the root or origin of the lattice. The number of nodes in the kth shell is given by


In some situations the definition is modified to specify that the root node has z − 1 neighbours.

Due to its distinctive topological structure, the statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

 of lattice models

Lattice model (physics)

In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...

 on this graph are often exactly solvable. The solutions are related to the often used Bethe approximation for these systems.

Relation to Cayley graphs

The Bethe lattice where each node is joined to 2n others is essentially the Cayley graph

Cayley graph

In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...

 of a free group

Free group

In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...

 on n generators.

A presentation of a group G by n generators corresponds to a surjective map from the free group on n generators to the group G, and at the level of Cayley graphs to a map from the Cayley tree to the Cayley graph. This can also be interpreted (in algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

) as the universal cover of the Cayley graph, which is not in general simply connected.

The distinction between a Bethe lattice and a Cayley tree is that the former is the thermodynamic limit of the latter. Hence in Cayley trees, surface effects become important.

Lattices in Lie groups

Bethe lattices also occur as the discrete group

Discrete group

In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...

 subgroups of certain hyperbolic Lie groups, such as the Fuchsian group

Fuchsian group

In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...

s. As such, they are also lattices in the sense of a lattice in a Lie group

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

.