
Regular local ring
Encyclopedia
In commutative algebra
, a regular local ring is a Noetherian
local ring
having the property that the minimal number of generators of its maximal ideal
is equal to its Krull dimension
. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of generators of m. Then in general n ≥ dim A, and A is defined to be regular if n = dim A.
The appellation regular is justified by the geometric meaning. A point x on a algebraic variety
X is nonsingular
if and only if the local ring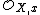 of germs
of germs
at x is regular. Regular local rings are not related to von Neumann regular ring
s.
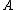 is a Noetherian local ring with maximal ideal
is a Noetherian local ring with maximal ideal  , then the following are equivalent definitions
, then the following are equivalent definitions
states that every regular local ring is a unique factorization domain
.
Every localization
of a regular local ring is regular.
The completion
of a regular local ring is regular.
If is a complete regular local ring that contains a field, then
is a complete regular local ring that contains a field, then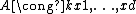 ,
,
where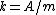 is the residue field
is the residue field
, and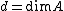 , the Krull dimension.
, the Krull dimension.
in 1937, but they first became prominent in the work of Oscar Zariski
a few years later, who showed that geometrically, a regular local ring corresponds to a smooth point on an algebraic variety
. Let Y be an algebraic variety
contained in affine n-space, and suppose that Y is the vanishing locus of the polynomials f1,...,fm. Y is nonsingular at P if Y satisfies a Jacobian
condition: If M = (∂fi/∂xj) is the matrix of partial derivatives of the defining equations of the variety, then the rank of the matrix found by evaluating M at P is n − dim Y. Zariski proved that Y is nonsingular at P if and only if the local ring of Y at P is regular. This implies that smoothness is an intrinsic property of the variety, in other words it does not depend on where or how the variety is embedded in affine space. It also suggests that regular local rings should have good properties, but before the introduction of techniques from homological algebra
very little was known in this direction. Once such techniques were introduced in the 1950s, Auslander and Buchsbaum proved that every regular local ring is a unique factorization domain
.
Another property suggested by geometric intuition is that the localization of a regular local ring should again be regular. Geometrically, this corresponds to the intuition that if a surface contains a curve, and that curve is smooth, then the surface is smooth near the curve. Again, this lay unsolved until the introduction of homological techniques. However, Jean-Pierre Serre
found a homological characterization of regular local rings: A local ring A is regular if and only if A has finite global dimension
. It is easy to show that the property of having finite global dimension is preserved under localization, and consequently that localizations of regular local rings at prime ideals are again regular. This allows us to define regularity for all rings, not just local ones: A ring A is said to be a regular ring
if its localizations at all of its prime ideals are regular local rings. It is equivalent to say that A has finite global dimension.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, a regular local ring is a Noetherian
Noetherian
In mathematics, the adjective Noetherian is used to describe objects that satisfy an ascending or descending chain condition on certain kinds of subobjects; in particular,* Noetherian group, a group that satisfies the ascending chain condition on subgroups...
local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
having the property that the minimal number of generators of its maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
is equal to its Krull dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
. In symbols, let A be a Noetherian local ring with maximal ideal m, and suppose a1, ..., an is a minimal set of generators of m. Then in general n ≥ dim A, and A is defined to be regular if n = dim A.
The appellation regular is justified by the geometric meaning. A point x on a algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
X is nonsingular
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
if and only if the local ring
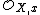 of germs
of germsGerm (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
at x is regular. Regular local rings are not related to von Neumann regular ring
Von Neumann regular ring
In mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
s.
Characterizations
There are a number of useful definitions of a regular local ring, one of which is mentioned above. In particular, if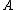 is a Noetherian local ring with maximal ideal
is a Noetherian local ring with maximal ideal  , then the following are equivalent definitions
, then the following are equivalent definitions
- Let
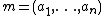 where
where  is chosen as small as possible. Then
is chosen as small as possible. Then 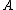 is regular if
is regular if
-
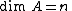 ,
,
- where the dimension is the Krull dimension. The minimal set of generators of
 are then called a regular system of parameters.
are then called a regular system of parameters.
- Let
 be the residue field of
be the residue field of 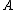 . Then
. Then 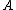 is regular if
is regular if
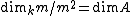 ,
,
- Let
- where the second dimension is the Krull dimensionKrull dimensionIn commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
.- Let
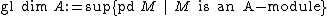 be the global dimensionGlobal dimensionIn ring theory and homological algebra, the global dimension of a ring A denoted gl dim A, is a non-negative integer or infinity which is a homological invariant of the ring. It is defined to be the supremum of the set of projective dimensions of all A-modules...
be the global dimensionGlobal dimensionIn ring theory and homological algebra, the global dimension of a ring A denoted gl dim A, is a non-negative integer or infinity which is a homological invariant of the ring. It is defined to be the supremum of the set of projective dimensions of all A-modules...
of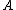 (i.e., the supremum of the projective dimensions of all
(i.e., the supremum of the projective dimensions of all  -modules.) Then
-modules.) Then 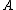 is regular if
is regular if
 ,
,
- Let
- in which case,
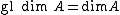 .
.
Examples
- Every fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is a regular local ring. These have (Krull) dimension 0. In fact, the fields are exactly the regular local rings of dimension 0. - Any discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
is a regular local ring of dimension 1 and the regular local rings of dimension 1 are exactly the discrete valuation rings. Specifically, if k is a field and X is an indeterminate, then the ring of formal power seriesFormal power seriesIn mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
kX is a regular local ring having (Krull) dimension 1. - If p is an ordinary prime number, the ring of p-adic integers is an example of a discrete valuation ring, and consequently a regular local ring, which does not contain a field.
- More generally, if k is a field and X1, X2, ..., Xd are indeterminates, then the ring of formal power series k
X1, X2, ..., Xd is a regular local ring having (Krull) dimension d. - If A is a regular ring, then it follows that the polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
A[x] and the formal power seriesFormal power seriesIn mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
ring Ax are both regular. - If Z is the ring of integers and X is an indeterminate, the ring Z[X](2, X) is an example of a 2-dimensional regular local ring which does not contain a field.
Basic properties
The Auslander–Buchsbaum theoremAuslander–Buchsbaum theorem
In commutative algebra, the Auslander–Buchsbaum theorem states that regular local rings are unique factorization domains.The theorem was first proved by . They showed that regular local rings of dimension 3 are unique factorization domains, and had previously shown that this implies that all...
states that every regular local ring is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
.
Every localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of a regular local ring is regular.
The completion
Completion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
of a regular local ring is regular.
If
 is a complete regular local ring that contains a field, then
is a complete regular local ring that contains a field, then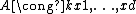 ,
,where
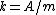 is the residue field
is the residue fieldResidue field
In mathematics, the residue field is a basic construction in commutative algebra. If R is a commutative ring and m is a maximal ideal, then the residue field is the quotient ring k = R/m, which is a field...
, and
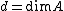 , the Krull dimension.
, the Krull dimension.Origin of Basic Notions
Regular local rings were originally defined by Wolfgang KrullWolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
in 1937, but they first became prominent in the work of Oscar Zariski
Oscar Zariski
Oscar Zariski was a Russian mathematician and one of the most influential algebraic geometers of the 20th century.-Education:...
a few years later, who showed that geometrically, a regular local ring corresponds to a smooth point on an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. Let Y be an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
contained in affine n-space, and suppose that Y is the vanishing locus of the polynomials f1,...,fm. Y is nonsingular at P if Y satisfies a Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
condition: If M = (∂fi/∂xj) is the matrix of partial derivatives of the defining equations of the variety, then the rank of the matrix found by evaluating M at P is n − dim Y. Zariski proved that Y is nonsingular at P if and only if the local ring of Y at P is regular. This implies that smoothness is an intrinsic property of the variety, in other words it does not depend on where or how the variety is embedded in affine space. It also suggests that regular local rings should have good properties, but before the introduction of techniques from homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
very little was known in this direction. Once such techniques were introduced in the 1950s, Auslander and Buchsbaum proved that every regular local ring is a unique factorization domain
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
.
Another property suggested by geometric intuition is that the localization of a regular local ring should again be regular. Geometrically, this corresponds to the intuition that if a surface contains a curve, and that curve is smooth, then the surface is smooth near the curve. Again, this lay unsolved until the introduction of homological techniques. However, Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
found a homological characterization of regular local rings: A local ring A is regular if and only if A has finite global dimension
Global dimension
In ring theory and homological algebra, the global dimension of a ring A denoted gl dim A, is a non-negative integer or infinity which is a homological invariant of the ring. It is defined to be the supremum of the set of projective dimensions of all A-modules...
. It is easy to show that the property of having finite global dimension is preserved under localization, and consequently that localizations of regular local rings at prime ideals are again regular. This allows us to define regularity for all rings, not just local ones: A ring A is said to be a regular ring
Regular ring
In commutative algebra, a regular ring is a commutative noetherian ring, such that the localization at every prime ideal is a regular local ring: that is, every such localization has the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension.Jean-Pierre...
if its localizations at all of its prime ideals are regular local rings. It is equivalent to say that A has finite global dimension.

