
Dirac operator
Encyclopedia
In mathematics
and quantum mechanics
, a Dirac operator is a differential operator
that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian. The original case which concerned Paul Dirac
was to factorise formally an operator for Minkowski space
, to get a form of quantum theory compatible with special relativity
; to get the relevant Laplacian as a product of first-order operators he introduced spinor
s.
In general, let be a first-order differential operator acting on a
be a first-order differential operator acting on a
vector bundle
 over a Riemannian manifold
over a Riemannian manifold
 .
.
If
with being the Laplacian of
being the Laplacian of  ,
,  is called a Dirac operator.
is called a Dirac operator.
In high-energy physics, this requirement is often relaxed: only the second-order part
of must equal the Laplacian.
must equal the Laplacian.
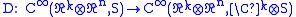
acting on spinor valued functions defined by
is sometimes called Dirac operator in k Clifford variables. In the notation, S is the space of spinors,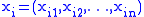 are n-dimensional variables and
are n-dimensional variables and 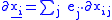 is the Dirac operator in the
is the Dirac operator in the 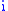 -th variable. This is a common generalization of the Dirac operator (k=1) and the Dolbeault operator
-th variable. This is a common generalization of the Dirac operator (k=1) and the Dolbeault operator
(n=2, k arbitrary). It is an invariant differential operator, invariant to the action of the group . The resolution of D is known only in some special cases.
. The resolution of D is known only in some special cases.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, a Dirac operator is a differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
that is a formal square root, or half-iterate, of a second-order operator such as a Laplacian. The original case which concerned Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
was to factorise formally an operator for Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, to get a form of quantum theory compatible with special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
; to get the relevant Laplacian as a product of first-order operators he introduced spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s.
In general, let
 be a first-order differential operator acting on a
be a first-order differential operator acting on avector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
 over a Riemannian manifold
over a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
 .
.If

with
 being the Laplacian of
being the Laplacian of  ,
,  is called a Dirac operator.
is called a Dirac operator.In high-energy physics, this requirement is often relaxed: only the second-order part
of
 must equal the Laplacian.
must equal the Laplacian.Examples
 is a Dirac operator on the tangent bundle over a line.
is a Dirac operator on the tangent bundle over a line.- We now consider a simple bundle of importance in physics: The configuration space of a particle with spin 1⁄2 confined to a plane, which is also the base manifold. It's represented by a a wavefunction ψ: R2 → C2
 ,
,
where x and y are the usual coordinate functions on R2. χ specifies the probability amplitudeProbability amplitudeIn quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
for the particle to be in the spin-up state, and similarly for η. The so-called spin-Dirac operator can then be written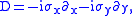
where σi are the Pauli matricesPauli matricesThe Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
. Note that the anticommutation relations for the Pauli matrices make the proof of the above defining property trivial. Those relations define the notion of a Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
.
Solutions to the Dirac equation for spinor fields are often called harmonic spinorshttp://eom.springer.de/S/s086780.htm. - The most famous Dirac operator describes the propagation of a free fermionFermionIn particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
in three dimensions and is elegantly written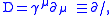
using the Feynman slash notationFeynman slash notationIn the study of Dirac fields in quantum field theory, Richard Feynman invented the convenient Feynman slash notation...
. - There is also the Dirac operator arising in Clifford analysisClifford analysisClifford analysis, using Clifford algebras named after William Kingdon Clifford, is the study of Dirac operators, and Dirac type operators in analysis and geometry, together with their applications...
. In euclidean n-space this is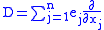
where
is an orthonormal basis for euclidean n-space, and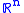 is considered to be embedded in a Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
is considered to be embedded in a Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
.
This is a special case of the Atiyah-Singer-Dirac operator acting on sections of a spinor bundle. - For a spin manifold, M, the Atiyah-Singer-Dirac operator is locally defined as follows: For
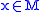 and
and  a local orthonormal basis for the tangent space of M at x, the Atiyah-Singer-Dirac operator is
a local orthonormal basis for the tangent space of M at x, the Atiyah-Singer-Dirac operator is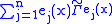 ,
,
where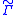 is a lifting of the Levi-Civita connection on M to the spinor bundle over M.
is a lifting of the Levi-Civita connection on M to the spinor bundle over M.
Generalisations
In Clifford analysis, the operator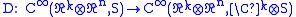
acting on spinor valued functions defined by

is sometimes called Dirac operator in k Clifford variables. In the notation, S is the space of spinors,
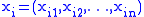 are n-dimensional variables and
are n-dimensional variables and 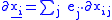 is the Dirac operator in the
is the Dirac operator in the 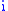 -th variable. This is a common generalization of the Dirac operator (k=1) and the Dolbeault operator
-th variable. This is a common generalization of the Dirac operator (k=1) and the Dolbeault operatorDolbeault cohomology
In mathematics, in particular in algebraic geometry and differential geometry, Dolbeault cohomology is an analog of de Rham cohomology for complex manifolds. Let M be a complex manifold...
(n=2, k arbitrary). It is an invariant differential operator, invariant to the action of the group
 . The resolution of D is known only in some special cases.
. The resolution of D is known only in some special cases.See also
- Dirac equationDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Clifford analysisClifford analysisClifford analysis, using Clifford algebras named after William Kingdon Clifford, is the study of Dirac operators, and Dirac type operators in analysis and geometry, together with their applications...
- ConnectionConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
- Dolbeault operator
- Heat kernelHeat kernelIn the mathematical study of heat conduction and diffusion, a heat kernel is the fundamental solution to the heat equation on a particular domain with appropriate boundary conditions. It is also one of the main tools in the study of the spectrum of the Laplace operator, and is thus of some...
- Spinor bundle

