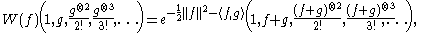CCR and CAR algebras
Encyclopedia
In Mathematics
and Physics
the CCR and CAR algebras arise from the study of canonical commutation relation
s in Boson
ic and Fermion
ic quantum mechanics
. They are used in mathematical formulations of quantum statistical mechanics and quantum field theory.
 be a real
be a real
vector space
equipped with a nonsingular real antisymmetric
bilinear form (i.e. a symplectic vector space
(i.e. a symplectic vector space
). The unital *-algebra generated by elements of subject to the relations
subject to the relations
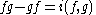
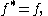
for any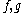 in
in  is called the canonical commutation relations (CCR) algebra. The uniqueness of the representations of this algebra when
is called the canonical commutation relations (CCR) algebra. The uniqueness of the representations of this algebra when 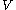 is finite dimension
is finite dimension
al is discussed in the Stone-von Neumann theorem.
If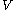 is equipped with a nonsingular real symmetric bilinear form
is equipped with a nonsingular real symmetric bilinear form
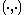 instead, the unital *-algebra generated by the elements of
instead, the unital *-algebra generated by the elements of 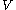 subject to the relations
subject to the relations
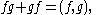
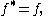
for any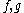 in
in 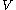 is called the canonical anticommutation relations (CAR) algebra.
is called the canonical anticommutation relations (CAR) algebra.
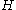 be a real symplectic vector space with nonsingular symplectic form
be a real symplectic vector space with nonsingular symplectic form 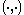 . In the theory of operator algebra
. In the theory of operator algebra
s the CCR algebra over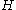 is the unital C*-algebra generated by elements
is the unital C*-algebra generated by elements 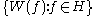 subject to
subject to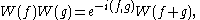
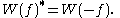
These are called the Weyl form of the canonical commutation relations and, in particular, they imply that each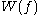 is unitary
is unitary
and . It is well known that the CCR algebra is a simple non-separable algebra and is unique up to isomorphism.
. It is well known that the CCR algebra is a simple non-separable algebra and is unique up to isomorphism.
When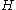 is a Hilbert space
is a Hilbert space
and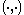 is given by the imaginary part of the inner-product, the CCR algebra is faithfully represented
is given by the imaginary part of the inner-product, the CCR algebra is faithfully represented
on the symmetric Fock space
over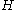 by setting
by setting
for any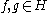 . The field operators
. The field operators 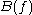 are defined for each
are defined for each 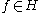 as the generator
as the generator
of the one-parameter unitary group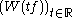 on the symmetric Fock space. These are self-adjoint
on the symmetric Fock space. These are self-adjoint
unbounded operator
s, however they formally satisfy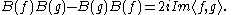
As the assignment is real-linear, so the operators
is real-linear, so the operators 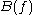 define a CCR algebra over
define a CCR algebra over 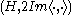 in the sense of Section 1.
in the sense of Section 1.
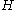 be a Hilbert space. In the theory of operator algebras the CAR algebra is the unique C*-completion of the complex unital *-algebra generated by elements
be a Hilbert space. In the theory of operator algebras the CAR algebra is the unique C*-completion of the complex unital *-algebra generated by elements 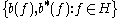 subject to the relations
subject to the relations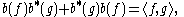

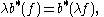
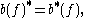
for any ,
,  .
.
When is separable the CAR algebra is an AF algebra and in the special case
is separable the CAR algebra is an AF algebra and in the special case 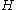 is infinite dimensional it is often written as
is infinite dimensional it is often written as 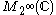 .
.
Let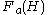 be the antisymmetric Fock space
be the antisymmetric Fock space
over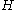 and let
and let 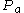 be the orothogonal projection onto antisymmetric vectors:
be the orothogonal projection onto antisymmetric vectors: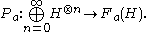
The CAR algebra is faithfully represented on by setting
by setting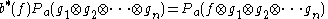
for all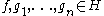 and
and 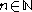 . The fact that these form a C*-algebra is due to the fact that creation and annihilation operators on antisymmetric Fock space are bona-fide bounded operator
. The fact that these form a C*-algebra is due to the fact that creation and annihilation operators on antisymmetric Fock space are bona-fide bounded operator
s. Moreover the field operators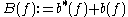 satisfy
satisfy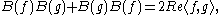
giving the relationship with Section 1
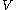 be a real
be a real 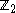 -graded vector space
-graded vector space
equipped with a nonsingular antisymmetric bilinear superform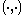 (i.e.
(i.e. 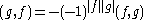 ) such that
) such that 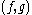 is real if either
is real if either 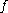 or
or 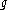 is an even element and imaginary
is an even element and imaginary
if both of them are odd. The unital *-algebra generated by the elements of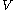 subject to the relations
subject to the relations

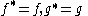
for any two pure elements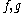 in
in 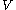 is the obvious superalgebra
is the obvious superalgebra
generalization which unifies CCRs with CARs: if all pure elements are even, one obtains a CCR, while if all pure elements are odd, one obtains a CAR.
The graded generalizations of Weyl and Clifford algebras allow the basis-free formulation of the canonical commutation and anticommutation relations in terms of a symplectic and a symmetric non-degenerate bilinear form. In addition the binary elements in this graded Weyl-algebra give a basis-free version of the commutation relations of the symplectic and pseudo-orthognal Lie algebras.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and Physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
the CCR and CAR algebras arise from the study of canonical commutation relation
Canonical commutation relation
In physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...
s in Boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic and Fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. They are used in mathematical formulations of quantum statistical mechanics and quantum field theory.
CCR and CAR as *-algebras
Let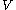 be a real
be a realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
equipped with a nonsingular real antisymmetric
Antisymmetric
The word antisymmetric refers to a change to an opposite quantity when another quantity is symmetrically changed. This concept is related to that of Symmetry and Asymmetry. The difference between these three concepts can be simply illustrated with Latin letters. The character "A" is symmetric about...
bilinear form
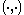 (i.e. a symplectic vector space
(i.e. a symplectic vector spaceSymplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
). The unital *-algebra generated by elements of
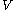 subject to the relations
subject to the relations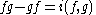
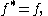
for any
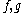 in
in  is called the canonical commutation relations (CCR) algebra. The uniqueness of the representations of this algebra when
is called the canonical commutation relations (CCR) algebra. The uniqueness of the representations of this algebra when 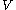 is finite dimension
is finite dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al is discussed in the Stone-von Neumann theorem.
If
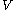 is equipped with a nonsingular real symmetric bilinear form
is equipped with a nonsingular real symmetric bilinear formSymmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
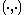 instead, the unital *-algebra generated by the elements of
instead, the unital *-algebra generated by the elements of 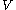 subject to the relations
subject to the relations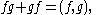
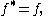
for any
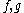 in
in 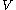 is called the canonical anticommutation relations (CAR) algebra.
is called the canonical anticommutation relations (CAR) algebra.The C*-algebra of CCR
Let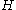 be a real symplectic vector space with nonsingular symplectic form
be a real symplectic vector space with nonsingular symplectic form 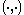 . In the theory of operator algebra
. In the theory of operator algebraOperator algebra
In functional analysis, an operator algebra is an algebra of continuous linear operators on a topological vector space with the multiplication given by the composition of mappings...
s the CCR algebra over
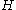 is the unital C*-algebra generated by elements
is the unital C*-algebra generated by elements 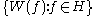 subject to
subject to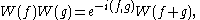
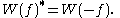
These are called the Weyl form of the canonical commutation relations and, in particular, they imply that each
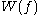 is unitary
is unitaryUnitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
and
 . It is well known that the CCR algebra is a simple non-separable algebra and is unique up to isomorphism.
. It is well known that the CCR algebra is a simple non-separable algebra and is unique up to isomorphism.When
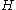 is a Hilbert space
is a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and
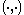 is given by the imaginary part of the inner-product, the CCR algebra is faithfully represented
is given by the imaginary part of the inner-product, the CCR algebra is faithfully representedRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
on the symmetric Fock space
Fock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
over
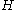 by setting
by setting
for any
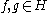 . The field operators
. The field operators 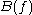 are defined for each
are defined for each 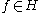 as the generator
as the generatorStone's theorem on one-parameter unitary groups
In mathematics, Stone's theorem on one-parameter unitary groups is a basic theorem of functional analysis which establishes a one-to-one correspondence between self-adjoint operators on a Hilbert space H and one-parameter families of unitary operators...
of the one-parameter unitary group
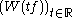 on the symmetric Fock space. These are self-adjoint
on the symmetric Fock space. These are self-adjointSelf-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
unbounded operator
Unbounded operator
In mathematics, more specifically functional analysis and operator theory, the notion of unbounded operator provides an abstract framework for dealing with differential operators, unbounded observables in quantum mechanics, and other cases....
s, however they formally satisfy
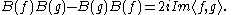
As the assignment
 is real-linear, so the operators
is real-linear, so the operators 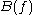 define a CCR algebra over
define a CCR algebra over 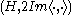 in the sense of Section 1.
in the sense of Section 1.The C*-algebra of CAR
Let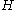 be a Hilbert space. In the theory of operator algebras the CAR algebra is the unique C*-completion of the complex unital *-algebra generated by elements
be a Hilbert space. In the theory of operator algebras the CAR algebra is the unique C*-completion of the complex unital *-algebra generated by elements 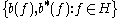 subject to the relations
subject to the relations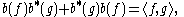

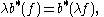
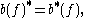
for any
 ,
,  .
.When
 is separable the CAR algebra is an AF algebra and in the special case
is separable the CAR algebra is an AF algebra and in the special case 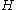 is infinite dimensional it is often written as
is infinite dimensional it is often written as 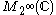 .
.Let
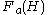 be the antisymmetric Fock space
be the antisymmetric Fock spaceFock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
over
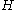 and let
and let 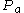 be the orothogonal projection onto antisymmetric vectors:
be the orothogonal projection onto antisymmetric vectors: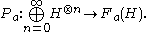
The CAR algebra is faithfully represented on
 by setting
by setting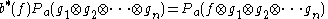
for all
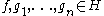 and
and 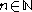 . The fact that these form a C*-algebra is due to the fact that creation and annihilation operators on antisymmetric Fock space are bona-fide bounded operator
. The fact that these form a C*-algebra is due to the fact that creation and annihilation operators on antisymmetric Fock space are bona-fide bounded operatorBounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s. Moreover the field operators
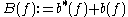 satisfy
satisfy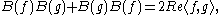
giving the relationship with Section 1
Superalgebra generalization
Let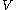 be a real
be a real 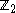 -graded vector space
-graded vector spaceGraded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
equipped with a nonsingular antisymmetric bilinear superform
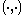 (i.e.
(i.e. 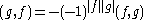 ) such that
) such that 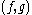 is real if either
is real if either 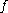 or
or 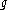 is an even element and imaginary
is an even element and imaginaryImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
if both of them are odd. The unital *-algebra generated by the elements of
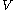 subject to the relations
subject to the relations
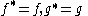
for any two pure elements
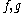 in
in 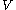 is the obvious superalgebra
is the obvious superalgebraSuperalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
generalization which unifies CCRs with CARs: if all pure elements are even, one obtains a CCR, while if all pure elements are odd, one obtains a CAR.
The graded generalizations of Weyl and Clifford algebras allow the basis-free formulation of the canonical commutation and anticommutation relations in terms of a symplectic and a symmetric non-degenerate bilinear form. In addition the binary elements in this graded Weyl-algebra give a basis-free version of the commutation relations of the symplectic and pseudo-orthognal Lie algebras.
See also
- canonical commutation relationCanonical commutation relationIn physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...
- Stone-von Neumann theorem
- Bose-Einstein statistics
- Fermi-Dirac statisticsFermi-Dirac statisticsFermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
- Heisenberg group
- Weyl algebra
- Bogoliubov transformationBogoliubov transformationIn theoretical physics, the Bogoliubov transformation, named after Nikolay Bogolyubov, is a unitary transformation from a unitary representation of some canonical commutation relation algebra or canonical anticommutation relation algebra into another unitary representation, induced by an...
- (−1)F(-1)^FIn a quantum field theory with fermions, F is a unitary, Hermitian, involutive operator which multiplies bosonic states by 1 and fermionic states by −1. This is always a global internal symmetry of any quantum field theory with fermions and corresponds to a rotation by 2π. This splits the Hilbert...