Dual quaternion
Encyclopedia
The set of dual quaternions is an algebra that can be used to represent spatial rigid body displacements. A dual quaternion is an ordered pair of quaternions  = (A, B) and therefore is constructed from eight real parameters. Because rigid body displacements are defined by six parameters, dual quaternion parameters include two algebraic constraints.
W. R. Hamilton introduced quaternion
s in 1843 and by 1873 W. K. Clifford
obtained a broad generalization of these numbers that he called biquaternions, which is an example of what is now called a Clifford algebra
. At the turn of the 20th century, Aleksandr Kotelnikov
and E. Study developed dual vectors and dual quaternions for use in the study of mechanics.
In ring theory
, dual quaternions are a ring (mathematics)
constructed in the same way as the quaternion
s, except using dual number
s instead of real number
s as coefficients. A dual quaternion can be represented in the form q = q0 + ε qε, where q0 and qε are ordinary quaternions and ε is the dual unit (εε = 0). Unlike quaternions they do not form a division ring
.
Similar to the way that rotations in 3D space can be represented by quaternions of unit length, rigid motions in 3D space can be represented by dual quaternions of unit length. This fact is used in theoretical kinematics
(see McCarthy), and in applications to 3D computer graphics
, robot
ics and computer vision
.
In 1891 Eduard Study
realized that this associative algebra
was ideal for describing the group of motions of three-dimensional space
. He further developed the idea in Geometrie der Dynamen in 1901. B. L. van der Waerden called the structure "Study biquaternions", one of three eight-dimensional algebras referred to as biquaternions.
s.
A quaternion is a linear combinations of the basis elements 1, i, j, and k. Hamilton's product rule for i, j, and k is often written as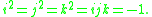
Compute i(ijk)=-jk=-i, to obtain jk=i, and (ijk)k=-ij=-k or ij=k. Now because j(jk)=ji=-k, we see that this product yields ij=-ji, which links quaternions to the properties of determinants.
A convenient way to work with the quaternion product is to write a quaternion as the sum of a scalar and a vector, that is A = a0 + A, where a0 is a real number and A = A1i + A2j + A3k is a three dimensional vector. The vector dot and cross operations can now be used to define the quaternion product of A=a0+A and C=c0+C as
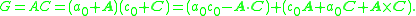
A dual quaternion is usually described as a quaternion with dual numbers as coefficients. A dual number
is an ordered pair â=(a, b). Two dual numbers add componentwise and multiply by the rule âĉ=(a, b)(c, d) = (ac, ad + bc). Dual numbers are often written in the form â=a+εb, where ε is the dual unit that commutes with i, j, k and has the property ε2=0.
The result is that a dual quaternion is the ordered pair of quaternions Â=(A, B). Two dual quaternions add componentwise and multiply by the rule,
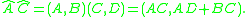
It is convenient to write a dual quaternion as the sum of a dual scalar and a dual vector, Â = â0 + A, where â0=(a, b) and A=(A, B) is the dual vector that defines a screw
. This notation allows us to write the product of two dual quaternions as
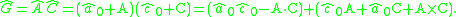
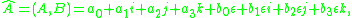
and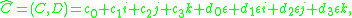
then
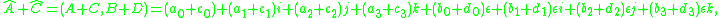
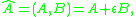
and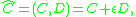
then
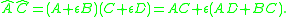
Notice that there is no BD term, because the definition of dual numbers requires that ε2 = 0.
This gives us the multiplication table (note the multiplication order is row times column):
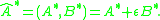
As for quaternions, the conjugate of the product of dual quaternions, Ĝ = ÂĈ, is the product of their conjugates in reverse order,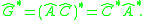
It is useful to introduce the functions Sc(∗) and Vec(∗) that select the scalar and vector parts of a quaternion, or the dual scalar and dual vector parts of a dual quaternion. In particular, if  = â0 + A, then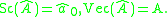
This allows the definition of the conjugate of  as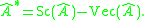
or,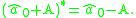
The product of a dual quaternion with its conjugate yields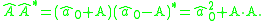
This is a dual scalar which is the magnitude squared of the dual quaternion.
Dual quaternions of magnitude 1 are used to represent spatial Euclidean displacements. Notice that the requirement that ÂÂ* = 1, introduces two algebraic constraints on the components of Â, that is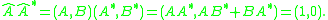
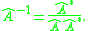
This is the dual version of the inverse of a quaternion.
and dual angle of the composite displacement DC=DBDA.
In general, the dual quaternion associated with a spatial displacement D = ([A],d) is constructed from its screw axis
S={S, V) and the dual angle (φ, d) where φ is the rotation about and d the slide along this axis, which defines the displacement D. The associated dual quaternion is given by,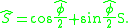
Let the composition of the displacement DB with DA be the displacement DC=DBDA. The screw axis and dual angle of DC is obtained from the product of the dual quaternions of DA and DB, given by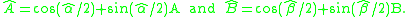
That is, the composite displacement DC=DBDA has the associated dual quaternion given by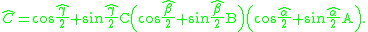
Expand this product in order to obtain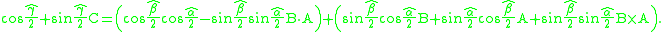
Divide both sides of this equation by the identity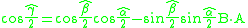
to obtain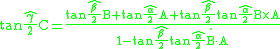
This is Rodrigues formula for the screw axis of a composite displacement defined in terms of the screw axes of the two displacements. He derived this formula in 1840.
The three screw axes A, B, and C form a spatial triangle and the dual angles at these vertices between the common normals that form the sides of this triangle are directly related to the dual angles of the three spatial displacements.
The quaternion product AC is a linear transformation by the operator A of the components of the quaternion C, therefore there is a matrix representation of A operating on the vector formed from the components of C.
Assemble the components of the quaternion C=c0+C into the array C=(C1, C2, C3, c0). Notice that the components of the vector part of the quaternion are listed first and the scalar is listed last. This is an arbitrary choice, but once this convention is selected we must abide by it.
The quaternion product AC can now be represented as the matrix product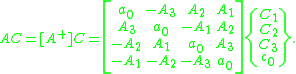
The product AC can also be viewed as an operation by C on the components of A, in which case we have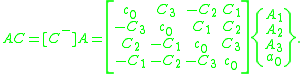
The dual quaternion product ÂĈ = (A, B)(C, D) = (AC, AD+BC) can be formulated as a matrix operation as follows. Assemble the components of Ĉ into the eight dimensional array Ĉ = (C1, C2, C3, c0, D1, D2, D3, d0), then ÂĈ is given by the 8x8 matrix product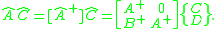
As we saw for quaternions, the product ÂĈ can be viewed as the operation of Ĉ on the coordinate vector Â, which means ÂĈ can also be formulated as,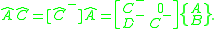
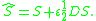
Let the Plucker coordinates of a line in the direction x through a point p in a moving body and its coordinates in the fixed frame which is in the direction X through the point P be given by,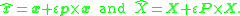
Then the dual quaternion of the displacement of this body transforms Plucker coordinates in the moving frame to Plucker coordinates in the fixed frame by the formula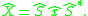
Using the matrix form of the dual quaternion product this becomes,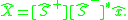
This calculation is easily managed using matrix operations.
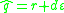where r and d are both quaternions. The r quaternion is known as the real or rotational part and the 
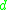quaternion is known as the dual or displacement part. A 3 dimensional position vector,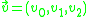
can be transformed by constructing the dual-quaternion representation,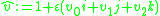
then a transformation by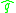
is given by
.
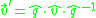The rotation part can be given by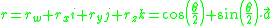
where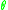
is the angle of rotation about axis 
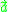. The rotation part can be expressed as a 3×3 orthogonal matrix
by
W. R. Hamilton introduced quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s in 1843 and by 1873 W. K. Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
obtained a broad generalization of these numbers that he called biquaternions, which is an example of what is now called a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
. At the turn of the 20th century, Aleksandr Kotelnikov
Aleksandr Kotelnikov
Aleksandr Petrovich Kotelnikov was a Russian mathematician specializing in geometric algebra.Kotelnikov graduated from Kazan University in 1884 and began teaching at a gymnasium. He began graduate work in mechanics and started instructing at the university in 1893. For his doctorate in 1899 he...
and E. Study developed dual vectors and dual quaternions for use in the study of mechanics.
In ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, dual quaternions are a ring (mathematics)
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
constructed in the same way as the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s, except using dual number
Dual number
In linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
s instead of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s as coefficients. A dual quaternion can be represented in the form q = q0 + ε qε, where q0 and qε are ordinary quaternions and ε is the dual unit (εε = 0). Unlike quaternions they do not form a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
.
Similar to the way that rotations in 3D space can be represented by quaternions of unit length, rigid motions in 3D space can be represented by dual quaternions of unit length. This fact is used in theoretical kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
(see McCarthy), and in applications to 3D computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, robot
Robot
A robot is a mechanical or virtual intelligent agent that can perform tasks automatically or with guidance, typically by remote control. In practice a robot is usually an electro-mechanical machine that is guided by computer and electronic programming. Robots can be autonomous, semi-autonomous or...
ics and computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
.
In 1891 Eduard Study
Eduard Study
Eduard Study was a German mathematician known for work on invariant theory of ternary forms and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.Study was born in Coburg in the Duchy of...
realized that this associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
was ideal for describing the group of motions of three-dimensional space
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
. He further developed the idea in Geometrie der Dynamen in 1901. B. L. van der Waerden called the structure "Study biquaternions", one of three eight-dimensional algebras referred to as biquaternions.
Formulas
In order to describe operations with dual quaternions, it is helpful to first consider quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s.
A quaternion is a linear combinations of the basis elements 1, i, j, and k. Hamilton's product rule for i, j, and k is often written as
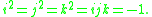
Compute i(ijk)=-jk=-i, to obtain jk=i, and (ijk)k=-ij=-k or ij=k. Now because j(jk)=ji=-k, we see that this product yields ij=-ji, which links quaternions to the properties of determinants.
A convenient way to work with the quaternion product is to write a quaternion as the sum of a scalar and a vector, that is A = a0 + A, where a0 is a real number and A = A1i + A2j + A3k is a three dimensional vector. The vector dot and cross operations can now be used to define the quaternion product of A=a0+A and C=c0+C as
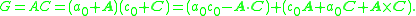
A dual quaternion is usually described as a quaternion with dual numbers as coefficients. A dual number
Dual number
In linear algebra, the dual numbers extend the real numbers by adjoining one new element ε with the property ε2 = 0 . The collection of dual numbers forms a particular two-dimensional commutative unital associative algebra over the real numbers. Every dual number has the form z = a + bε with a and...
is an ordered pair â=(a, b). Two dual numbers add componentwise and multiply by the rule âĉ=(a, b)(c, d) = (ac, ad + bc). Dual numbers are often written in the form â=a+εb, where ε is the dual unit that commutes with i, j, k and has the property ε2=0.
The result is that a dual quaternion is the ordered pair of quaternions Â=(A, B). Two dual quaternions add componentwise and multiply by the rule,
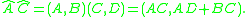
It is convenient to write a dual quaternion as the sum of a dual scalar and a dual vector, Â = â0 + A, where â0=(a, b) and A=(A, B) is the dual vector that defines a screw
Screw theory
Screw theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....
. This notation allows us to write the product of two dual quaternions as
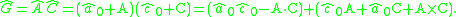
Addition
The addition of dual quaternions is defined componentwise so that given,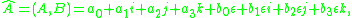and
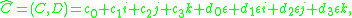
then
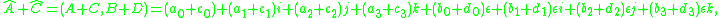
Multiplication
Multiplication of two dual quaternion follows from the multiplication rules for the quaternion units i, j, k and commutative multiplication by the dual unit ε. In particular, given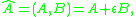and
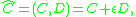
then
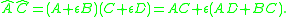
Notice that there is no BD term, because the definition of dual numbers requires that ε2 = 0.
This gives us the multiplication table (note the multiplication order is row times column):
| × | 1 | i | j | k | ε | εi | εj | εk |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | i | j | k | ε | εi | εj | εk |
| i | i | −1 | k | −j | εi | −ε | εk | −εj |
| j | j | −k | −1 | i | εj | −εk | −ε | εi |
| k | k | j | −i | −1 | εk | εj | −εi | −ε |
| ε | ε | εi | εj | εk | 0 | 0 | 0 | 0 |
| εi | εi | −ε | εk | −εj | 0 | 0 | 0 | 0 |
| εj | εj | −εk | −ε | εi | 0 | 0 | 0 | 0 |
| εk | εk | εj | −εi | −ε | 0 | 0 | 0 | 0 |
Conjugate
The conjugate of a dual quaternion is the extension of the conjugate of a quaternion, that is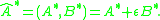As for quaternions, the conjugate of the product of dual quaternions, Ĝ = ÂĈ, is the product of their conjugates in reverse order,
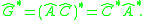
It is useful to introduce the functions Sc(∗) and Vec(∗) that select the scalar and vector parts of a quaternion, or the dual scalar and dual vector parts of a dual quaternion. In particular, if  = â0 + A, then
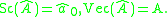
This allows the definition of the conjugate of  as
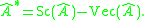
or,
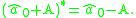
The product of a dual quaternion with its conjugate yields
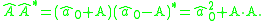
This is a dual scalar which is the magnitude squared of the dual quaternion.
Norm
The norm of a dual quaternion |Â| is computed using the conjugate to compute |Â| = √(ÂÂ*). This is a dual number called the magnitude of the dual quaternion. Dual quaternions with |Â| = 1 are unit dual quaternions.Dual quaternions of magnitude 1 are used to represent spatial Euclidean displacements. Notice that the requirement that ÂÂ* = 1, introduces two algebraic constraints on the components of Â, that is
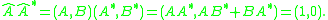
Inverse
The inverse of a dual quaternion is defined as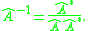This is the dual version of the inverse of a quaternion.
Dual quaternions and spatial displacements
A benefit of the dual quaternion formulation of the composition of two spatial displacements DB=([RB], b) and DA=([RA],a) is that the resulting dual quaternion yields directly the screw axisScrew axis
The screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
and dual angle of the composite displacement DC=DBDA.
In general, the dual quaternion associated with a spatial displacement D = ([A],d) is constructed from its screw axis
Screw axis
The screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
S={S, V) and the dual angle (φ, d) where φ is the rotation about and d the slide along this axis, which defines the displacement D. The associated dual quaternion is given by,
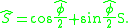
Let the composition of the displacement DB with DA be the displacement DC=DBDA. The screw axis and dual angle of DC is obtained from the product of the dual quaternions of DA and DB, given by
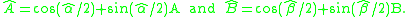
That is, the composite displacement DC=DBDA has the associated dual quaternion given by
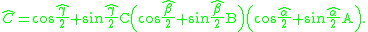
Expand this product in order to obtain
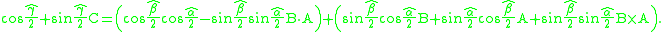
Divide both sides of this equation by the identity
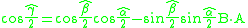
to obtain
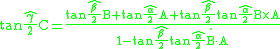
This is Rodrigues formula for the screw axis of a composite displacement defined in terms of the screw axes of the two displacements. He derived this formula in 1840.
The three screw axes A, B, and C form a spatial triangle and the dual angles at these vertices between the common normals that form the sides of this triangle are directly related to the dual angles of the three spatial displacements.
Matrix form of dual quaternion multiplication
The matrix representation of the quaternion product is convenient for programming quaternion computations using matrix algebra, which is true for dual quaternion operations as well.The quaternion product AC is a linear transformation by the operator A of the components of the quaternion C, therefore there is a matrix representation of A operating on the vector formed from the components of C.
Assemble the components of the quaternion C=c0+C into the array C=(C1, C2, C3, c0). Notice that the components of the vector part of the quaternion are listed first and the scalar is listed last. This is an arbitrary choice, but once this convention is selected we must abide by it.
The quaternion product AC can now be represented as the matrix product
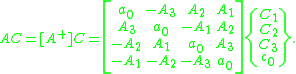
The product AC can also be viewed as an operation by C on the components of A, in which case we have
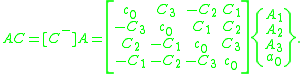
The dual quaternion product ÂĈ = (A, B)(C, D) = (AC, AD+BC) can be formulated as a matrix operation as follows. Assemble the components of Ĉ into the eight dimensional array Ĉ = (C1, C2, C3, c0, D1, D2, D3, d0), then ÂĈ is given by the 8x8 matrix product
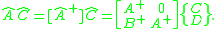
As we saw for quaternions, the product ÂĈ can be viewed as the operation of Ĉ on the coordinate vector Â, which means ÂĈ can also be formulated as,
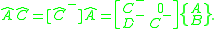
More on spatial displacements
The dual quaternion of a displacement D=([A], d) can be constructed from the quaternion S=cos(φ/2) + sin(φ/2)S that defines the rotation [A] and the vector quaternion constructed from the translation vector d, given by D = d1i + d2j + d3k. Using this notation, the dual quaternion for the displacement D=([A], d) is given by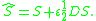Let the Plucker coordinates of a line in the direction x through a point p in a moving body and its coordinates in the fixed frame which is in the direction X through the point P be given by,
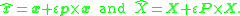
Then the dual quaternion of the displacement of this body transforms Plucker coordinates in the moving frame to Plucker coordinates in the fixed frame by the formula
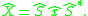
Using the matrix form of the dual quaternion product this becomes,
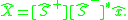
This calculation is easily managed using matrix operations.
Dual quaternions and 4x4 homogeneous transforms
It might be helpful, especially in rigid body motion, to represent dual quaternions as homogeneous matrices. As given above a dual quaternion can be written as: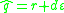 where r and d are both quaternions. The r quaternion is known as the real or rotational part and the 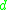quaternion is known as the dual or displacement part. A 3 dimensional position vector,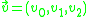can be transformed by constructing the dual-quaternion representation,
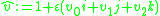
then a transformation by
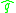is given by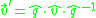.The rotation part can be given by
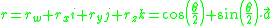
where
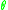is the angle of rotation about axis 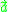. The rotation part can be expressed as a 3×3 orthogonal matrixOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
by
-
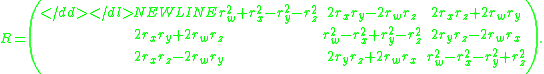
The displacement can be written as-
.
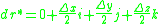Translation and rotation combined in one transformation matrix is:-
Where the left upper 3×3 matrix is the rotation matrix we just calculated.
Eponyms
Since both Eduard StudyEduard StudyEduard Study was a German mathematician known for work on invariant theory of ternary forms and for the study of spherical trigonometry. He is also known for contributions to space geometry, hypercomplex numbers, and criticism of early physical chemistry.Study was born in Coburg in the Duchy of...
and William Kingdon CliffordWilliam Kingdon CliffordWilliam Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
used, and wrote upon, the dual quaternions, at times authors refer to dual biquaternions as “Study biquaternions” or “Clifford biquaternions”. The latter eponymEponymAn eponym is the name of a person or thing, whether real or fictitious, after which a particular place, tribe, era, discovery, or other item is named or thought to be named...
has also been used to refer to split-biquaternions. Read the article by Joe Rooney linked below for view of a supporter of W.K. Clifford’s claim. Since the claims of Clifford and Study are in contention, it is convenient to use the current designation dual quaternion to avoid conflict.
See also
- Screw theoryScrew theoryScrew theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....
- Screw axisScrew axisThe screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
- QuaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
- Rational motionRational motionIn kinematics, the motion of a rigid body is defined as a continuous set of displacements. One-parameter motions can be definedas a continuous displacement of moving object with respect to a fixed frame in Euclidean three-space , where the displacement depends on one parameter, mostly identified as...
- Quaternions and spatial rotationQuaternions and spatial rotationUnit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
- Biquaternion
- Conversion between quaternions and Euler anglesConversion between quaternions and Euler anglesSpatial rotations in three dimensions can be parametrized using both Euler angles and unit quaternions. This article explains how to convert between the two representations. Actually this simple use of "quaternions" was first presented by Euler some seventy years earlier than Hamilton to solve the...
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Olinde RodriguesOlinde RodriguesBenjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
- Screw theory
-