Baire space
Encyclopedia
In mathematics
, a Baire space is a topological space
which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire
who introduced the concept.
s with empty
interior
consists precisely of the boundaries
of dense
open set
s. These sets are, in a certain sense, "negligible".
Some examples are finite sets, smooth curve
s in the plane, and proper affine subspaces in a Euclidean space
. A topological space is a Baire space if it is "large", meaning that it is not a countable union
of negligible subsets. For example, the three dimensional Euclidean space is not a countable union of its affine planes.
of any countable collection
of closed set
s with empty
interior
has empty interior.
This definition is equivalent to each of the following conditions:
) as follows.
A subset of a topological space X is called
The definition for a Baire space can then be stated as follows: a topological space X is a Baire space if every non-empty open set is of second category in X. This definition is equivalent to the modern definition.
A subset A of X is comeagre if its complement
is meagre. A topological space X is a Baire space if and only if every comeager subset of X is dense.
gives sufficient conditions for a topological space to be a Baire space. It is an important tool in topology
and functional analysis
.
BCT1 shows that each of the following is a Baire space:
BCT2 shows that every manifold
is a Baire space, even if it is not paracompact, and hence not metrizable. For example, the long line
is of second category.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Baire space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire
René-Louis Baire
René-Louis Baire was a French mathematician most famous for his Baire category theorem, which helped to generalize and prove future theorems...
who introduced the concept.
Motivation
In an arbitrary topological space, the class of closed setClosed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s with empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
consists precisely of the boundaries
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s. These sets are, in a certain sense, "negligible".
Some examples are finite sets, smooth curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s in the plane, and proper affine subspaces in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. A topological space is a Baire space if it is "large", meaning that it is not a countable union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of negligible subsets. For example, the three dimensional Euclidean space is not a countable union of its affine planes.
Definition
The precise definition of a Baire space has undergone slight changes throughout history, mostly due to prevailing needs and viewpoints. First, we give the usual modern definition, and then we give a historical definition which is closer to the definition originally given by Baire.Modern definition
A topological space is called a Baire space if the unionUnion (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of any countable collection
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s with empty
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
has empty interior.
This definition is equivalent to each of the following conditions:
- Every intersection of countably many denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s is dense. - The interior of every unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of countably many closedClosedClosed may refer to:Math* Closure * Closed manifold* Closed orbits* Closed set* Closed differential form* Closed map, a function that is closed.Other* Cloister, a closed walkway* Closed-circuit television...
nowhere dense sets is empty. - Whenever the union of countably many closed subsets of X has an interior point, then one of the closed subsets must have an interior point.
Historical definition
In his original definition, Baire defined a notion of category (unrelated to category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
) as follows.
A subset of a topological space X is called
- nowhere denseNowhere dense setIn mathematics, a nowhere dense set in a topological space is a set whose closure has empty interior. The order of operations is important. For example, the set of rational numbers, as a subset of R has the property that the closure of the interior is empty, but it is not nowhere dense; in fact it...
in X if the interiorInterior (topology)In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of its closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
is emptyEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced... - of first category or meagreMeagre setIn the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
in X if it is a union of countably many nowhere dense subsets - of second category or nonmeagre in X if it is not of first category in X
The definition for a Baire space can then be stated as follows: a topological space X is a Baire space if every non-empty open set is of second category in X. This definition is equivalent to the modern definition.
A subset A of X is comeagre if its complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
is meagre. A topological space X is a Baire space if and only if every comeager subset of X is dense.Examples
- The space R of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with the usual topology, is a Baire space, and so is of second category in itself. The rational numbers are of first category and the irrational numbers are of second category in R. - The Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is a Baire space, and so is of second category in itself, but it is of first category in the interval [0, 1] with the usual topology. - Here is an example of a set of second category in R with Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
0.
- where
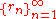is a sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
that enumerates the rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s.- Note that the space of rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s with the usual topology inherited from the realsReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
is not a Baire space, since it is the union of countably many closed sets without interior, the singletons.
- Note that the space of rational number
Baire category theorem
The Baire category theoremBaire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
gives sufficient conditions for a topological space to be a Baire space. It is an important tool in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
- (BCT1) Every completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is a Baire space. More generally, every topological space which is homeomorphic to an open subsetOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of a completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
pseudometric spacePseudometric spaceIn mathematics, a pseudometric space is a generalized metric space in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space, every seminormed space is a pseudometric space...
is a Baire space. In particular, every topologically complete space is a Baire space. - (BCT2) Every locally compact Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is a Baire space.
BCT1 shows that each of the following is a Baire space:
- The space R of real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s - The space of irrational numbers
- The Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
- Indeed, every Polish spacePolish spaceIn the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
BCT2 shows that every manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is a Baire space, even if it is not paracompact, and hence not metrizable. For example, the long line
Long line (topology)
In topology, the long line is a topological space somewhat similar to the real line, but in a certain way "longer". It behaves locally just like the real line, but has different large-scale properties. Therefore it serves as one of the basic counterexamples of topology...
is of second category.
Properties
- Every non-empty Baire space is of second category in itself, and every intersection of countably many dense open subsets of X is non-empty, but the converse of neither of these is true, as is shown by the topological disjoint sum of the rationals and the unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0, 1].
- Every open subspace of a Baire space is a Baire space.
- Given a family of continuous functions fn:X→Y with pointwise limit f:X→Y. If X is a Baire space then the points where f is not continuous is a meagre setMeagre setIn the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
in X and the set of points where f is continuous is dense in X. A special case of this is the uniform boundedness principleUniform boundedness principleIn mathematics, the uniform boundedness principle or Banach–Steinhaus theorem is one of the fundamental results in functional analysis. Together with the Hahn–Banach theorem and the open mapping theorem, it is considered one of the cornerstones of the field...
.