
Symmetry in physics
Encyclopedia

Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, symmetry includes all features of a physical system
Physical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
that exhibit the property of symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation
Observation
Observation is either an activity of a living being, such as a human, consisting of receiving knowledge of the outside world through the senses, or the recording of data using scientific instruments. The term may also refer to any data collected during this activity...
. A symmetry of a physical system is a physical or mathematical feature of the system (observed or intrinsic) that is "preserved" under some change.
A family of particular transformations may be continuous (such as rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of a circle) or discrete
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
(e.g., reflection
Reflection (physics)
Reflection is the change in direction of a wavefront at an interface between two differentmedia so that the wavefront returns into the medium from which it originated. Common examples include the reflection of light, sound and water waves...
of a bilaterally symmetric figure, or rotation of a regular polygon). Continuous and discrete transformations give rise to corresponding types of symmetries. Continuous symmetries can be described by Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s while discrete symmetries are described by finite groups (see Symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
). Symmetries are frequently amenable to mathematical formulation such as group representations
Representation of a Lie group
In mathematics and theoretical physics, the idea of a representation of a Lie group plays an important role in the study of continuous symmetry. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie...
and can be exploited to simplify many problems.
An important example of such symmetry is the invariance
General covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
of the form of physical laws under arbitrary differentiable coordinate transformations.
Symmetry as invariance
Invariance is specified mathematically by transformations that leave some quantity unchanged. This idea can apply to basic real-world observations. For example, temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
may be constant throughout a room. Since the temperature is independent of position within the room, the temperature is invariant under a shift in the measurer's position.
Similarly, a uniform sphere rotated about its center will appear exactly as it did before the rotation. The sphere is said to exhibit spherical symmetry. A rotation about any axis of the sphere will preserve how the sphere "looks".
Invariance in force
The above ideas lead to the useful idea of invariance when discussing observed physical symmetry; this can be applied to symmetries in forces as well.For example, an electric field due to a wire is said to exhibit cylindrical symmetry, because the electric field strength at a given distance r from the electrically charged wire of infinite length will have the same magnitude at each point on the surface of a cylinder (whose axis is the wire) with radius r. Rotating the wire about its own axis does not change its position or charge density, hence it will preserve the field. The field strength at a rotated position is the same. Suppose some configuration of charges (may be non-stationary) produce an electric field in some direction, then rotating the configuration of the charges (without disturbing the internal dynamics that produces the particular field) will lead to a net rotation of the direction of the electric field.These two properties are interconnected through the more general property that rotating any system of charges causes a corresponding rotation of the electric field.
In Newton's theory of mechanics, given two bodies, each with mass m, starting from rest at the origin and moving along the x-axis in opposite directions, one with speed v1 and the other with speed v2 the total kinetic energy of the system (as calculated from an observer at the origin) is and remains the same if the velocities are interchanged. The total kinetic energy is preserved under a reflection in the y-axis.
The last example above illustrates another way of expressing symmetries, namely through the equations that describe some aspect of the physical system. The above example shows that the total kinetic energy will be the same if v1 and v2 are interchanged.
Local and global symmetries
Symmetries may be broadly classified as global or local. A global symmetry is one that holds at all points of spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
, whereas a local symmetry is one that has a different symmetry transformation at different points of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
; specifically a local symmetry transformation is parameterised by the spacetime co-ordinates. Local symmetries play an important role in physics as they form the basis for gauge theories
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
.
Continuous symmetries
The two examples of rotational symmetry described above - spherical and cylindrical - are each instances of continuous symmetryContinuous symmetry
In mathematics, continuous symmetry is an intuitive idea corresponding to the concept of viewing some symmetries as motions, as opposed to e.g. reflection symmetry, which is invariance under a kind of flip from one state to another. It has largely and successfully been formalised in the...
. These are characterised by invariance following a continuous change in the geometry of the system. For example, the wire may be rotated through any angle about its axis and the field strength will be the same on a given cylinder. Mathematically, continuous symmetries are described by continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
or smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s. An important subclass of continuous symmetries in physics are spacetime symmetries.
Spacetime symmetries
Continuous spacetime symmetries are symmetries involving transformations of spaceSpace
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
. These may be further classified as spatial symmetries, involving only the spatial geometry associated with a physical system; temporal symmetries, involving only changes in time; or spatio-temporal symmetries, involving changes in both space and time.
- Time translation: A physical system may have the same features over a certain interval of time
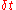 ; this is expressed mathematically as invariance under the transformation
; this is expressed mathematically as invariance under the transformation  for any real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
for any real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s t and a in the interval. For example, in classical mechanics, a particle solely acted upon by gravity will have gravitational potential energy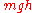 when suspended from a height
when suspended from a height 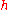 above the Earth's surface. Assuming no change in the height of the particle, this will be the total gravitational potential energy of the particle at all times. In other words, by considering the state of the particle at some time (in seconds)
above the Earth's surface. Assuming no change in the height of the particle, this will be the total gravitational potential energy of the particle at all times. In other words, by considering the state of the particle at some time (in seconds) 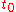 and also at
and also at  , say, the particle's total gravitational potential energy will be preserved.
, say, the particle's total gravitational potential energy will be preserved.
- Spatial translation: These spatial symmetries are represented by transformations of the form
 and describe those situations where a property of the system does not change with a continuous change in location. For example, the temperature in a room may be independent of where the thermometer is located in the room.
and describe those situations where a property of the system does not change with a continuous change in location. For example, the temperature in a room may be independent of where the thermometer is located in the room.
- Spatial rotation: These spatial symmetries are classified as proper rotations and improper rotationImproper rotationIn 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
s. The former are just the 'ordinary' rotations; mathematically, they are represented by square matrices with unit determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. The latter are represented by square matrices with determinant −1 and consist of a proper rotation combined with a spatial reflection (inversionPoint reflectionIn geometry, a point reflection or inversion in a point is a type of isometry of Euclidean space...
). For example, a sphere has proper rotational symmetry. Other types of spatial rotations are described in the article Rotation symmetry.
- Poincaré transformations: These are spatio-temporal symmetries which preserve distances in Minkowski spacetime, i.e. they are isometries of Minkowski space. They are studied primarily in special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. Those isometries that leave the origin fixed are called Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s and give rise to the symmetry known as Lorentz covarianceLorentz covarianceIn standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
.
- Projective symmetries: These are spatio-temporal symmetries which preserve the geodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
structure of spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. They may be defined on any smooth manifold, but find many applications in the study of exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
.
- Inversion transformations: These are spatio-temporal symmetries which generalise Poincaré transformations to include other conformal one-to-one transformations on the space-time coordinates. Lengths are not invariant under inversion transformations but there is a cross-ratio on four points that is invariant.
Mathematically, spacetime symmetries are usually described by smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s on a smooth manifold. The underlying local diffeomorphism
Local diffeomorphism
In mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
s associated with the vector fields correspond more directly to the physical symmetries, but the vector fields themselves are more often used when classifying the symmetries of the physical system.
Some of the most important vector fields are Killing vector field
Killing vector field
In mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
s which are those spacetime symmetries that preserve the underlying metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
structure of a manifold. In rough terms, Killing vector fields preserve the distance between any two points of the manifold and often go by the name of isometries. The article Isometries in physics discusses these symmetries in more detail.
Discrete symmetries
A discrete symmetry is a symmetry that describes non-continuous changes in a system. For example, a square possesses discrete rotational symmetry, as only rotations by multiples of right angles will preserve the square's original appearance. Discrete symmetries sometimes involve some type of 'swapping', these swaps usually being called reflections or interchanges.- Time reversalT-symmetryT Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries...
: Many laws of physics describe real phenomena when the direction of time is reversed. Mathematically, this is represented by the transformation, . For example, Newton's second law of motion still holds if, in the equation
. For example, Newton's second law of motion still holds if, in the equation  ,
,  is replaced by
is replaced by  . This may be illustrated by describing the motion of a particle thrown up vertically (neglecting air resistance). For such a particle, position is symmetric with respect to the instant that the object is at its maximum height. Velocity at reversed time is reversed.
. This may be illustrated by describing the motion of a particle thrown up vertically (neglecting air resistance). For such a particle, position is symmetric with respect to the instant that the object is at its maximum height. Velocity at reversed time is reversed.
- Spatial inversionParity (physics)In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
: These are represented by transformations of the form and indicate an invariance property of a system when the coordinates are 'inverted'.
and indicate an invariance property of a system when the coordinates are 'inverted'.
- Glide reflectionGlide reflectionIn geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
: These are represented by a composition of a translation and a reflection. These symmetries occur in some crystalCrystalA crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
s and in some planar symmetries, known as wallpaper symmetriesWallpaper groupA wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
.
C, P, and T symmetries
The Standard modelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
has three related natural near-symmetries. These state that the actual universe about us is indistinguishable from one where:
- Every particle is replaced with its antiparticleAntiparticleCorresponding to most kinds of particles, there is an associated antiparticle with the same mass and opposite electric charge. For example, the antiparticle of the electron is the positively charged antielectron, or positron, which is produced naturally in certain types of radioactive decay.The...
. This is C-symmetryC-symmetryIn physics, C-symmetry means the symmetry of physical laws under a charge-conjugation transformation. Electromagnetism, gravity and the strong interaction all obey C-symmetry, but weak interactions violate C-symmetry.-Charge reversal in electromagnetism:...
(charge symmetry); - Everything appears as if reflected in a mirror. This is P-symmetryParity (physics)In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
(parity symmetry); - The direction of timeEntropy (arrow of time)Entropy is the only quantity in the physical sciences that requires a particular direction for time, sometimes called an arrow of time. As one goes "forward" in time, the second law of thermodynamics says, the entropy of an isolated system will increase...
is reversed. This is T-symmetryT-symmetryT Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries...
(time symmetry).
T-symmetry is counterintuitive (surely the future and the past are not symmetrical) but explained by the fact that the Standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
describes local properties, not global ones like entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
. To properly reverse the direction of time, one would have to put the big bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
and the resulting low-entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
state in the "future." Since we perceive the "past" ("future") as having lower (higher) entropy than the present (see perception of time
Entropy (arrow of time)
Entropy is the only quantity in the physical sciences that requires a particular direction for time, sometimes called an arrow of time. As one goes "forward" in time, the second law of thermodynamics says, the entropy of an isolated system will increase...
), the inhabitants of this hypothetical time-reversed universe would perceive the future in the same way as we perceive the past.
These symmetries are near-symmetries because each is broken in the present-day universe. However, the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
predicts that the combination of the three (that is, the simultaneous application of all three transformations) must be a symmetry, called CPT symmetry
CPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
. CP violation
CP violation
In particle physics, CP violation is a violation of the postulated CP-symmetry: the combination of C-symmetry and P-symmetry . CP-symmetry states that the laws of physics should be the same if a particle were interchanged with its antiparticle , and left and right were swapped...
, the violation of the combination of C- and P-symmetry, is necessary for the presence of significant amounts of baryonic matter in the universe and thus is a prerequisite for the existence of life
Life
Life is a characteristic that distinguishes objects that have signaling and self-sustaining processes from those that do not, either because such functions have ceased , or else because they lack such functions and are classified as inanimate...
. CP violation is a fruitful area of current research in particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
.
Supersymmetry
A type of symmetry known as supersymmetry has been used to try to make theoretical advances in the standard modelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
. Supersymmetry is based on the idea that there is another physical symmetry beyond those already developed in the standard model, specifically a symmetry between boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s and fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s. Supersymmetry asserts that each type of boson has, as a supersymmetric partner, a fermion, called a superpartner, and vice versa. Supersymmetry has not yet been experimentally verified: no known particle has the correct properties to be a superpartner of any other known particle. If superpartners exist they must have masses greater than current particle accelerator
Particle accelerator
A particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams. An ordinary CRT television set is a simple form of accelerator. There are two basic types: electrostatic and oscillating field accelerators.In...
s can generate.
Mathematics of physical symmetry
The transformations describing physical symmetries typically form a mathematical groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
is an important area of mathematics for physicists.
Continuous symmetries are specified mathematically by continuous groups (called Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s). Many physical symmetries are isometries and are specified by symmetry groups. Sometimes this term is used for more general types of symmetries. The set of all proper rotations (about any angle) through any axis of a sphere form a Lie group called the special orthogonal group
 . (The 3 refers to the three-dimensional space of an ordinary sphere.) Thus, the symmetry group of the sphere with proper rotations is
. (The 3 refers to the three-dimensional space of an ordinary sphere.) Thus, the symmetry group of the sphere with proper rotations is  . Any rotation preserves distances on the surface of the ball. The set of all Lorentz transformations form a group called the Lorentz group
. Any rotation preserves distances on the surface of the ball. The set of all Lorentz transformations form a group called the Lorentz groupLorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
(this may be generalised to the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
).
Discrete symmetries are described by discrete groups. For example, the symmetries of an equilateral triangle are described by the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
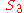 .
.An important type of physical theory based on local symmetries is called a gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
and the symmetries natural to such a theory are called gauge symmetries. Gauge symmetries in the Standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, used to describe three of the fundamental interaction
Fundamental interaction
In particle physics, fundamental interactions are the ways that elementary particles interact with one another...
s, are based on the SU(3) × SU(2) × U(1) group. (Roughly speaking, the symmetries of the SU(3) group describe the strong force, the SU(2) group describes the weak interaction
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
and the U(1) group describes the electromagnetic force.)
Also, the reduction by symmetry of the energy functional under the action by a group and spontaneous symmetry breaking
Spontaneous symmetry breaking
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
of transformations of symmetric groups appear to elucidate topics in particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
(for example, the unification of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
and the weak force in physical cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
).
Conservation laws and symmetry
The symmetry properties of a physical system are intimately related to the conservation laws characterizing that system. Noether's theoremNoether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
gives a precise description of this relation. The theorem states that each continuous symmetry of a physical system implies that some physical property of that system is conserved. Conversely, each conserved quantity has a corresponding symmetry. For example, the isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
gives rise to conservation of (linear) momentum, and isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
gives rise to conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
.
The following table summarizes some fundamental symmetries and the associated conserved quantity.
| Class | Invariance Invariant (physics) In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another... |
Conserved quantity Conservation law In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves.... |
| Proper orthochronous Lorentz symmetry |
translation in time (homogeneity Homogeneity (physics) In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity... ) |
energy Conservation of energy The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time... |
| translation in space (homogeneity Homogeneity (physics) In general, homogeneity is defined as the quality or state of being homogeneous . For instance, a uniform electric field would be compatible with homogeneity... ) |
linear momentum | |
| rotation in space Rotational invariance In mathematics, a function defined on an inner product space is said to have rotational invariance if its value does not change when arbitrary rotations are applied to its argument... (isotropy Isotropy Isotropy is uniformity in all orientations; it is derived from the Greek iso and tropos . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix an, hence anisotropy. Anisotropy is also used to describe situations where properties vary... ) |
angular momentum | |
| Discrete symmetry Discrete symmetry A discrete symmetry is a symmetry that describes non-continuous changes in a system. For example, a square possesses discrete rotational symmetry, as only rotations by multiples of right angles will preserve the square's original appearance. Discrete symmetries sometimes involve some type of... |
P, coordinate inversion |
spatial parity |
| C, charge conjugation |
charge parity | |
| T, time reversal |
time parity T-symmetry T Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries... |
|
| CPT CPT symmetry CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:... |
product of parities | |
| Internal symmetry (independent of spacetime Spacetime In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions... coordinates) |
U(1) gauge transformation |
electric charge Electric charge Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two... |
| U(1) gauge transformation |
lepton generation number Lepton number In particle physics, the lepton number is the number of leptons minus the number of antileptons.In equation form,so all leptons have assigned a value of +1, antileptons −1, and non-leptonic particles 0... |
|
| U(1) gauge transformation |
hypercharge Hypercharge In particle physics, the hypercharge Y of a particle is related to the strong interaction, and is distinct from the similarly named weak hypercharge, which has an analogous role in the electroweak interaction... |
|
| U(1)Y gauge transformation |
weak hypercharge Weak hypercharge The weak hypercharge in particle physics is a conserved quantum number relating the electrical charge and the third component of weak isospin, and is similar to the Gell-Mann–Nishijima formula for the hypercharge of strong interactions... |
|
| U(2) [U(1) × SU(2)] |
electroweak force | |
| SU(2) gauge transformation |
isospin Isospin In physics, and specifically, particle physics, isospin is a quantum number related to the strong interaction. This term was derived from isotopic spin, but the term is confusing as two isotopes of a nucleus have different numbers of nucleons; in contrast, rotations of isospin maintain the number... |
|
| SU(2)L gauge transformation |
weak isospin Weak isospin In particle physics, weak isospin is a quantum number relating to the weak interaction, and parallels the idea of isospin under the strong interaction. Weak isospin is usually given the symbol T or I with the third component written as Tz, T3, Iz or I3... |
|
| P × SU(2) |
G-parity G-parity In theoretical physics, G-parity is a multiplicative quantum number that results from the generalization of C-parity to multiplets of particles.... |
|
| SU(3) "winding number" |
baryon number | |
| SU(3) gauge transformation |
quark color | |
| SU(3) (approximate) |
quark flavor | |
| S(U(2) × U(3)) [ U(1) × SU(2) × SU(3)] |
Standard Model Standard Model The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon... |
|
See also
- Conservation lawConservation lawIn physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
- Conserved currentConserved currentIn physics a conserved current is a current, j^\mu, that satisfies the continuity equation \partial_\mu j^\mu=0. The continuity equation represents a conservation law, hence the name....
- Coordinate-free
- Covariance and contravarianceCovariance and contravarianceIn multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis from one coordinate system to another. When one coordinate system is just a rotation of the other, this...
- DiffeomorphismDiffeomorphismIn mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
- Fictitious forceFictitious forceA fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
- Galilean invarianceGalilean invarianceGalilean invariance or Galilean relativity is a principle of relativity which states that the fundamental laws of physics are the same in all inertial frames...
- Gauge theoryGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
- General covarianceGeneral covarianceIn theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
- Harmonic coordinate conditionHarmonic coordinate conditionThe harmonic coordinate condition is one of several coordinate conditions in general relativity, which make it possible to solve the Einstein field equations. A coordinate system is said to satisfy the harmonic coordinate condition if each of the coordinate functions xα satisfies d'Alembert's...
- Inertial frame of referenceInertial frame of referenceIn physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
- Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
- List of mathematical topics in relativity
- Lorentz covarianceLorentz covarianceIn standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
- Noether's theoremNoether's theoremNoether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
- Poincaré groupPoincaré groupIn physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
- Special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
- Spontaneous symmetry breakingSpontaneous symmetry breakingSpontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state....
- Standard modelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
- Standard model (mathematical formulation)
- Symmetry breakingSymmetry breakingSymmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
- Wheeler–Feynman Time-Symmetric Theory
General readers
- Leon Lederman and Christopher T. HillChristopher T. HillChristopher T. Hill is a theoretical physicist at the Fermi National Accelerator Laboratory. He did undergraduate work in physics at M.I.T. , and graduate work at Caltech...
(2005) Symmetry and the Beautiful Universe. Amherst NY: Prometheus Books. - Schumm, Bruce (2004) Deep Down Things. Johns Hopkins Univ. Press.
- Victor J. StengerVictor J. StengerVictor John Stenger is an American particle physicist, outspoken atheist, and author, now active in philosophy and popular religious skepticism....
(2000) Timeless Reality: Symmetry, Simplicity, and Multiple Universes. Buffalo NY: Prometheus Books. Chpt. 12 is a gentle introduction to symmetry, invariance, and conservation laws. - Anthony ZeeAnthony ZeeAnthony Zee is a Chinese American physicist, writer, and currently a professor at the Kavli Institute for Theoretical Physics and the physics department of the University of California, Santa Barbara.Zee obtained his Ph.D. from Harvard in 1970, supervised by Sidney Coleman...
(2007) Fearful Symmetry: The search for beauty in modern physics, 2nd ed. Princeton University Press. ISBN 978-0-691-00946-9. 1986 1st ed. published by Macmillan.
Technical
- Brading, K., and Castellani, E., eds. (2003) Symmetries in Physics: Philosophical Reflections. Cambridge Univ. Press.
- -------- (2007) "Symmetries and Invariances in Classical Physics" in Butterfield, J., and John EarmanJohn EarmanJohn Earman is a philosopher of physics. He is currently an emeritus professor in the History and Philosophy of Science department at the University of Pittsburgh. He has also taught at UCLA, the Rockefeller University, and the University of Minnesota, and was president of the Philosophy of...
, eds., Philosophy of Physic Part B. North Holland: 1331-68. - Debs, T. and Redhead, M. (2007) Objectivity, Invariance, and Convention: Symmetry in Physical Science. Harvard Univ. Press.
- John EarmanJohn EarmanJohn Earman is a philosopher of physics. He is currently an emeritus professor in the History and Philosophy of Science department at the University of Pittsburgh. He has also taught at UCLA, the Rockefeller University, and the University of Minnesota, and was president of the Philosophy of...
(2002) "Laws, Symmetry, and Symmetry Breaking: Invariance, Conservations Principles, and Objectivity." Address to the 2002 meeting of the Philosophy of Science AssociationPhilosophy of Science AssociationThe Philosophy of Science Association is an academic organization which promotes further studies and free discussion from diverse standpoints in the field of philosophy of science....
. - Mainzer, K. (1996) Symmetries of nature. Berlin: De Gruyter.
- Thompson, William J. (1994) Angular Momentum: An Illustrated Guide to Rotational Symmetries for Physical Systems. Wiley. ISBN 0-471-55264.
- Bas Van Fraassen (1989) Laws and symmetry. Oxford Univ. Press.
- Eugene Wigner (1967) Symmetries and Reflections. Indiana Univ. Press.
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: "Symmetry" -- by K. Brading and E. Castellani. - Pedagogic Aids to Quantum Field Theory Click on link to Chapter 6: Symmetry, Invariance, and Conservation for a simplified, step-by-step introduction to symmetry in physics.

